整数范围与类型转换

整数范围与类型转换

-2147483647-1 == 2147483648U
-2147483647-1 < -2147483647
-2147483647-1 < 2147483647
(unsigned)-2147483647-1 < 2147483647
上面四个表达式成立吗？为什么？并用C语言编程测试并提交运行截图。

代码

点击查看代码

#include<stdio.h>

void main(){
    if(-2147483647-1 ==  2147483648U)
    printf("true\n");
    else
    {
        printf("false\n");
    }
     if(-2147483647-1 < -2147483647)
    printf("true\n");
    else
    {
        printf("false\n");
    }
     if(-2147483647-1 <  2147483647)
    printf("true\n");
    else
    {
        printf("false\n");
    }
     if((unsigned)-2147483647-1 <  2147483647)
    printf("true\n");
    else
    {
        printf("false\n");
    }
    return 0;
}

运行结果

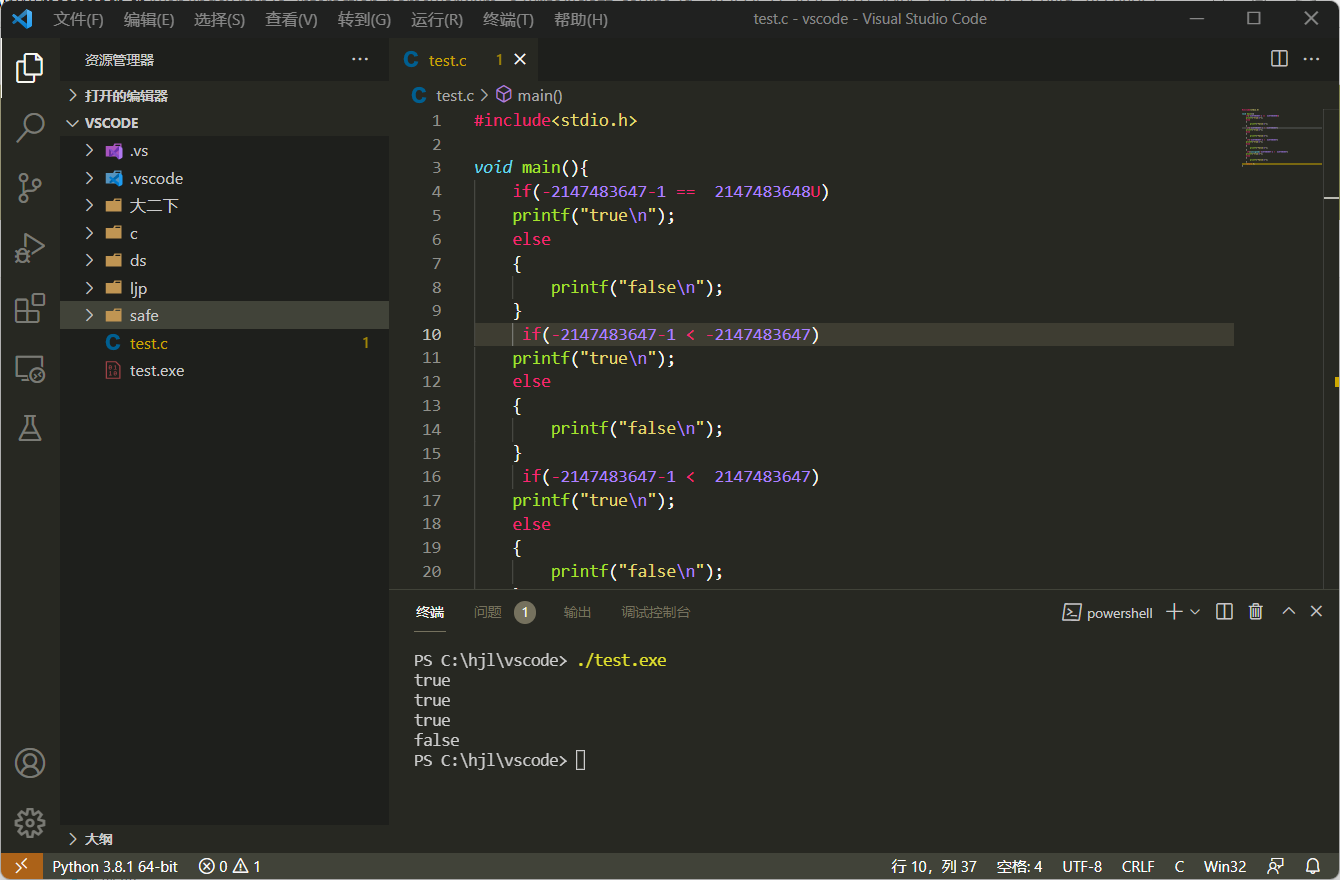
分析

负数 < 正数 负数u > 正数（负数u平移，到正数的上一半部分去了）

• -2147483647-1 < 2147483647 true常识
• -2147483647-1 > 2147483647u true 负数-->无符号数

等价于

• 2147483648 > 2147483647u
  (-2147483647-1 负数---->无符号数 = 2的32次-2147483648 = 2147483648 > 2147483647u）

负数 > 负数 负数u>负数u（负数u平移，仍然保持负数的大小规律）

• -1 > -2 true常识

• -1 > -2u true（-1，-2都转化为无符号数，但是还是要遵循-1>-2 ）
  转换为有符号数前后，都是-1>-2

• -2147483647-1 < -2147483647 true

• -2147483647-1 < -2147483647u true

总结

• -1u是转化为最大的无符号数4294967295

• -2147483648u是最小的无符号数2147483648
  仍然保持负数的大小规律
  -1 > -2147483647-1
  -1 u> -2147483647-1 u

• 为什么-2147483647-1 而不直接-2147483648

• -2147483648是一个常量表达式，而不是一个常量。所以-2147483648被理解为一个“-”号和一个常量值2147483648。对于“-”，是对原值补码进行“取反加1”操作。由于2147483648超出了有符号常量的表示范围，所以变成了unsigned long int或long long int，而写成-2147483647 - 1则可以精确的表示成为32位有符号整数的最小值。