哈夫曼树与哈夫曼编码
哈夫曼树与哈夫曼编码
哈夫曼博士
判断树:用于分类过程的二叉树.
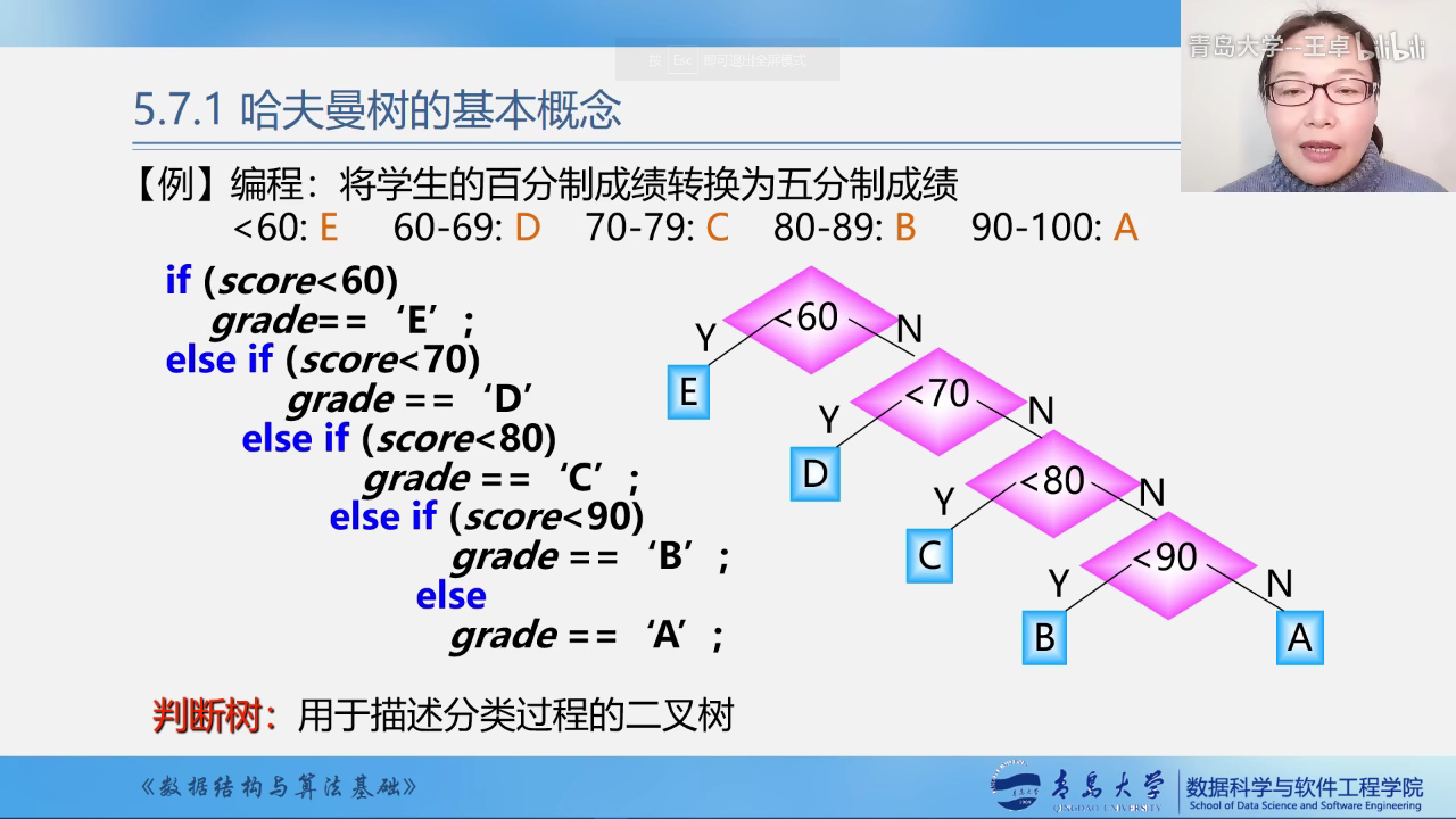
如果采用右面的方法建立二叉树则需要比较31500次
我们还可以采用左边的方法建立树需要比较22000次
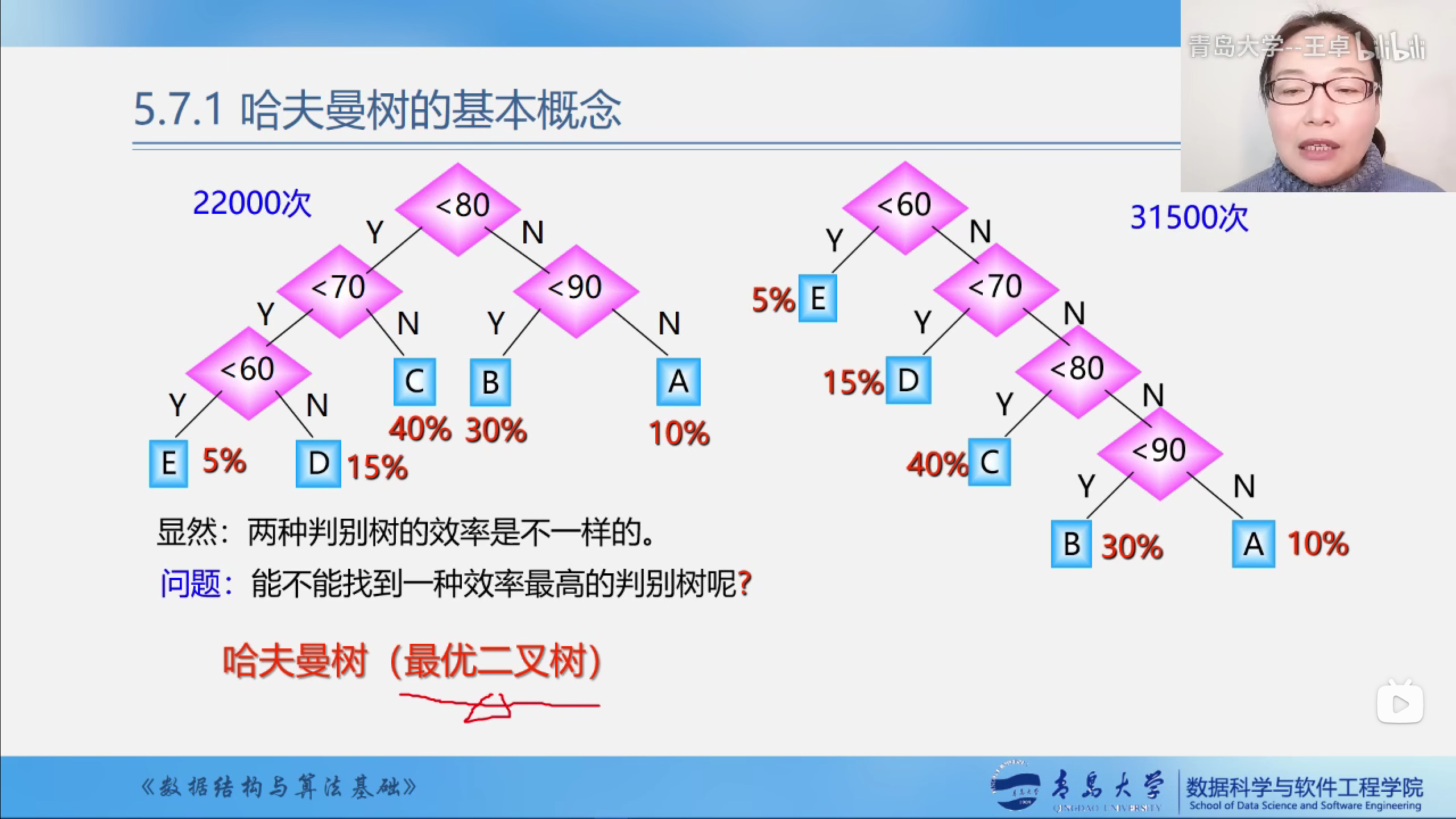
显然两种判别树的效率是不一样的
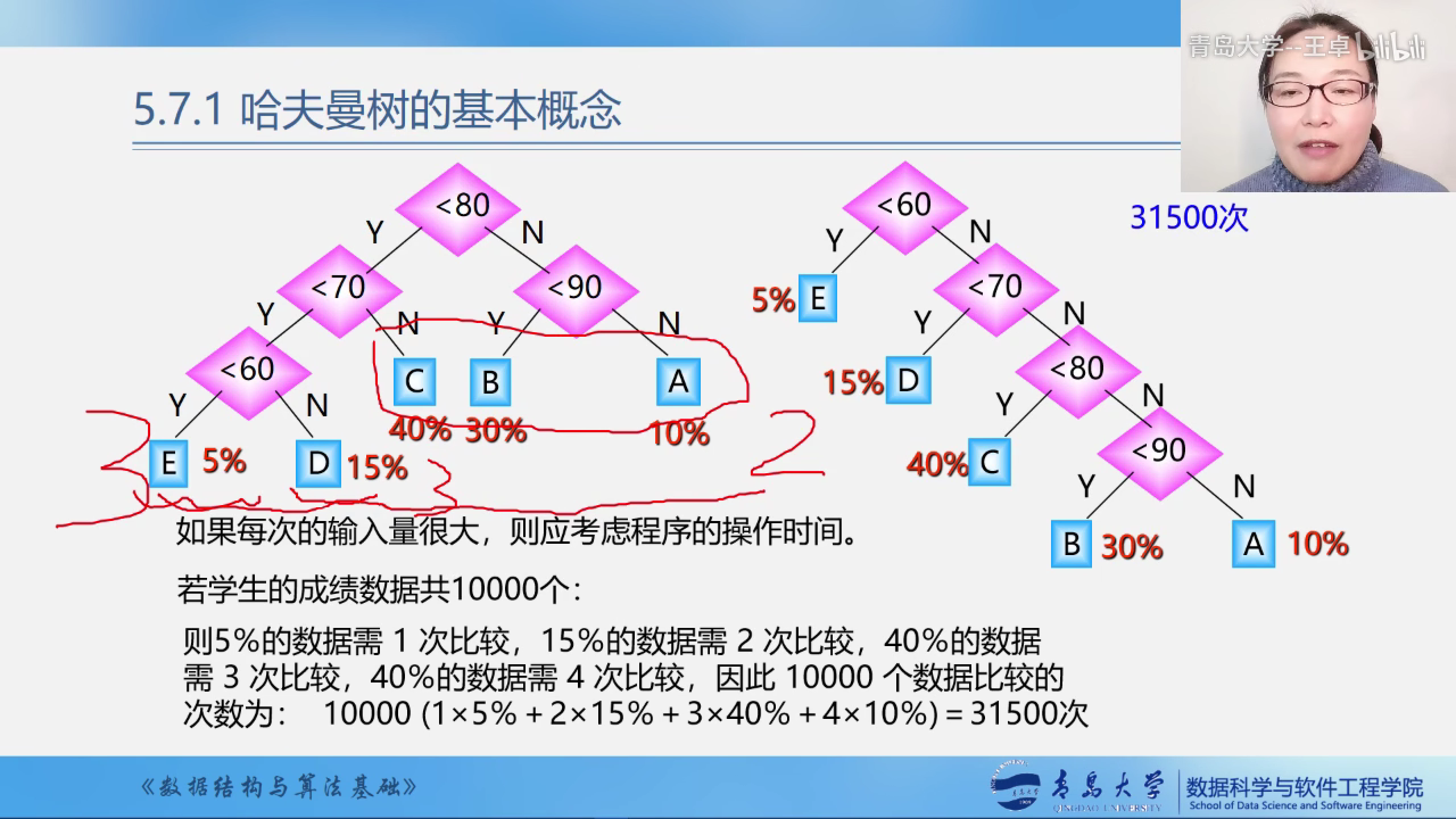
如何找到效率最高的判别树?
这就是哈夫曼树(最优二叉树)
哈夫曼树的基本概念
- 路径
- 结点的路径长度
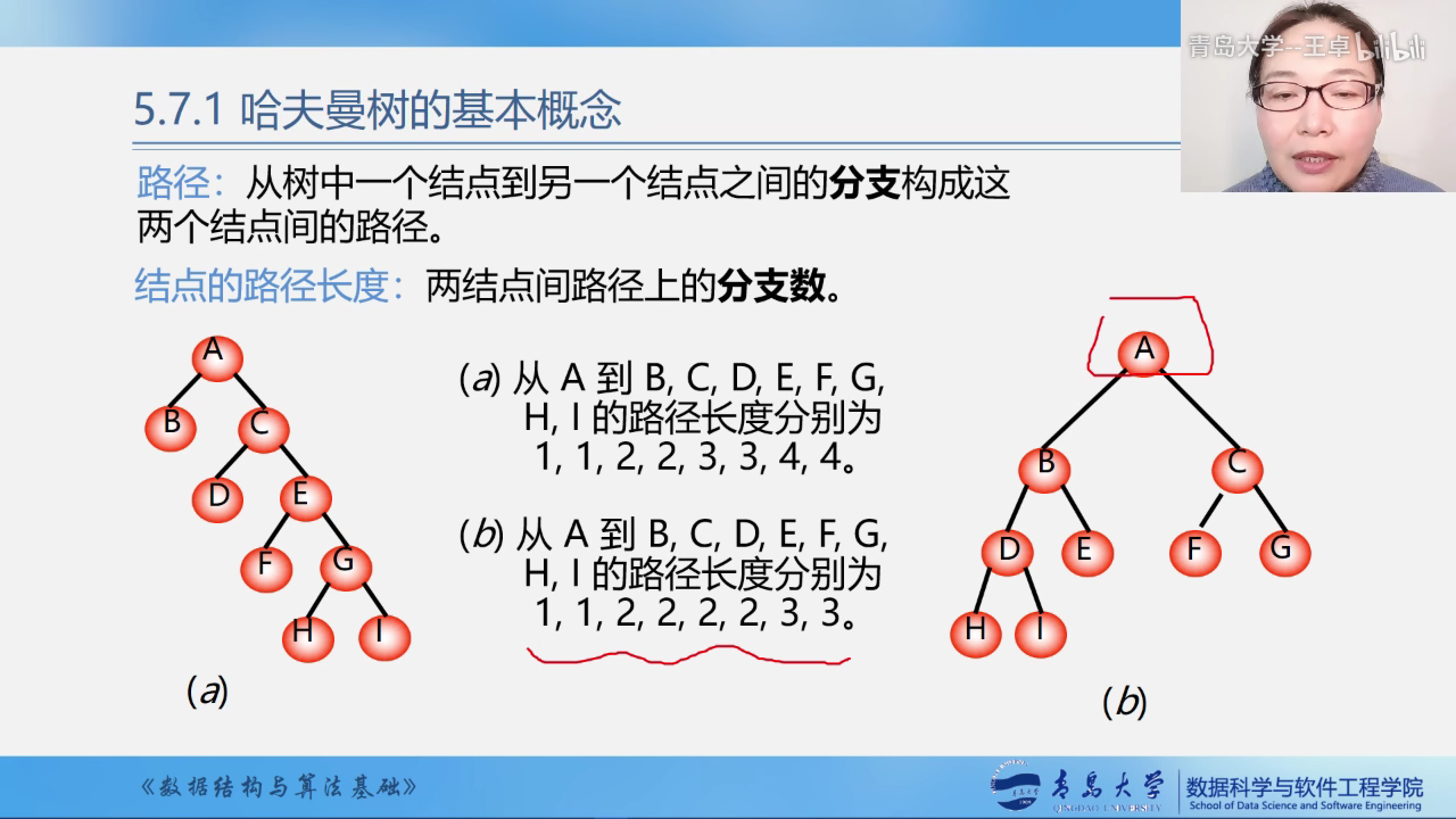
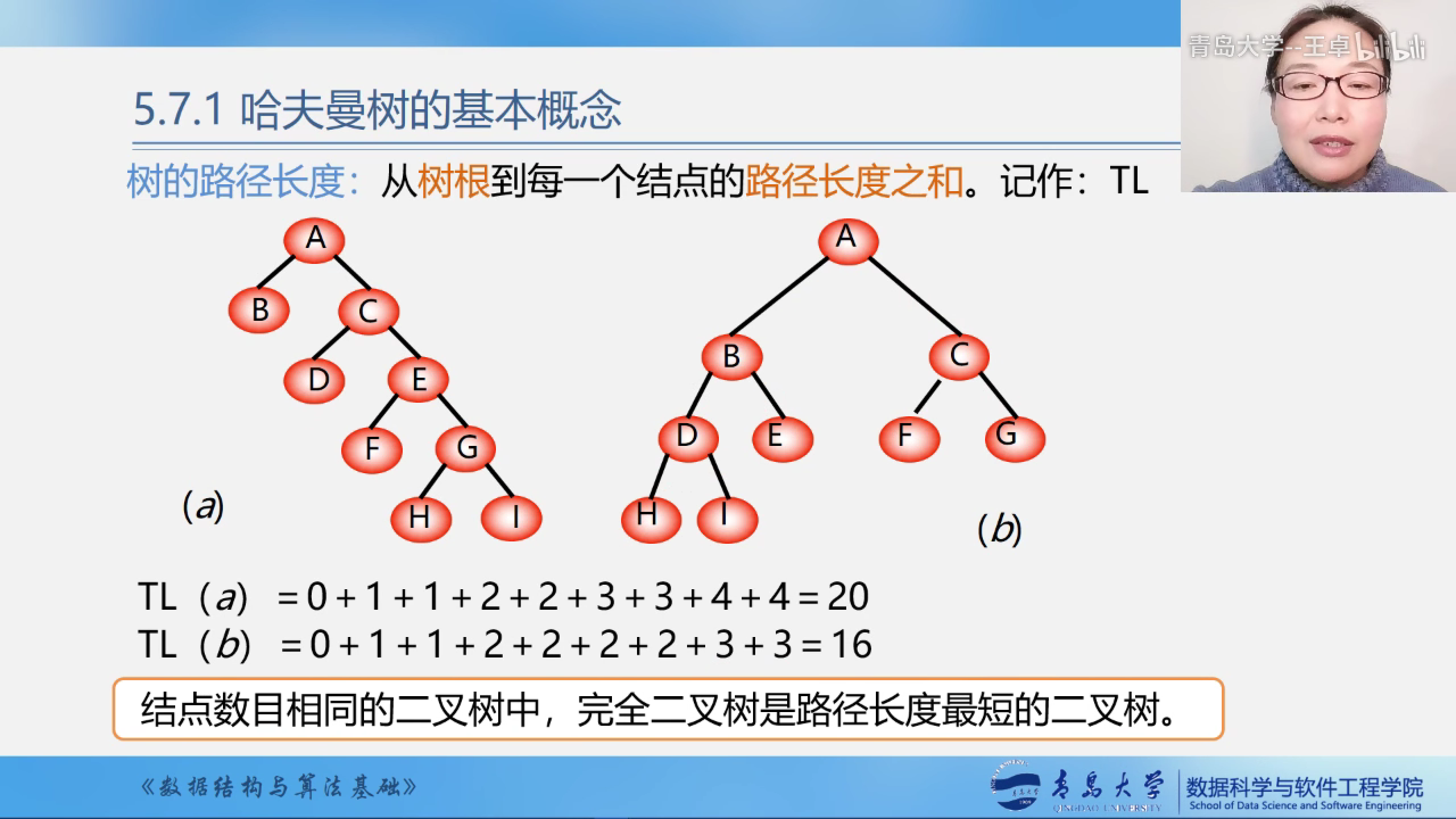
树的路径长度
从树根到每一个结点的路径长度之和.记作:TL
完全二叉树的路径长度最短,但路径最短的二叉树不一定是完全二叉树.
因为完全二叉树的结点层次是最小的.
几个重要概念
- 权
- 结点的带权路径长度
- 树的带权路径长度
例子
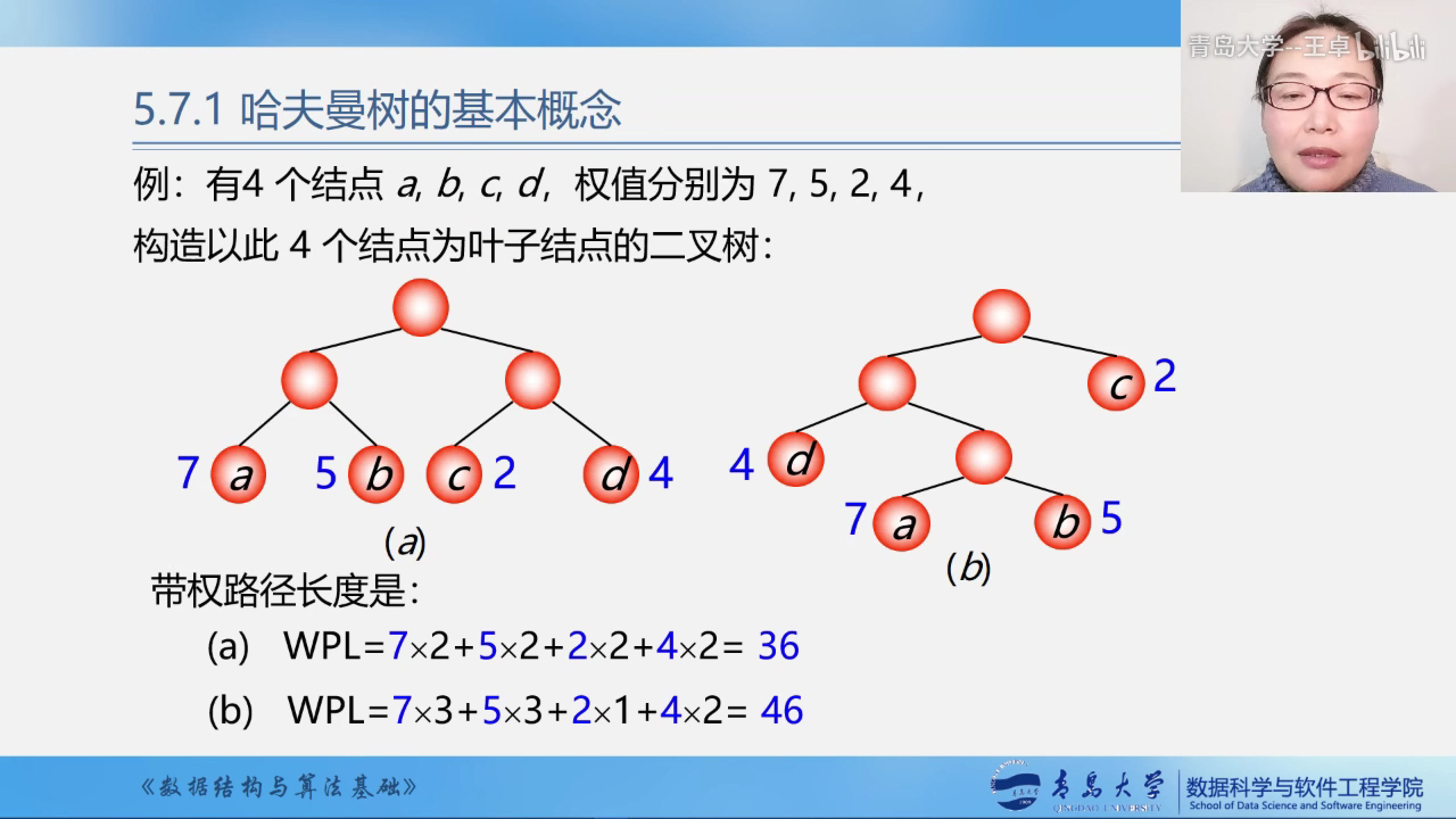
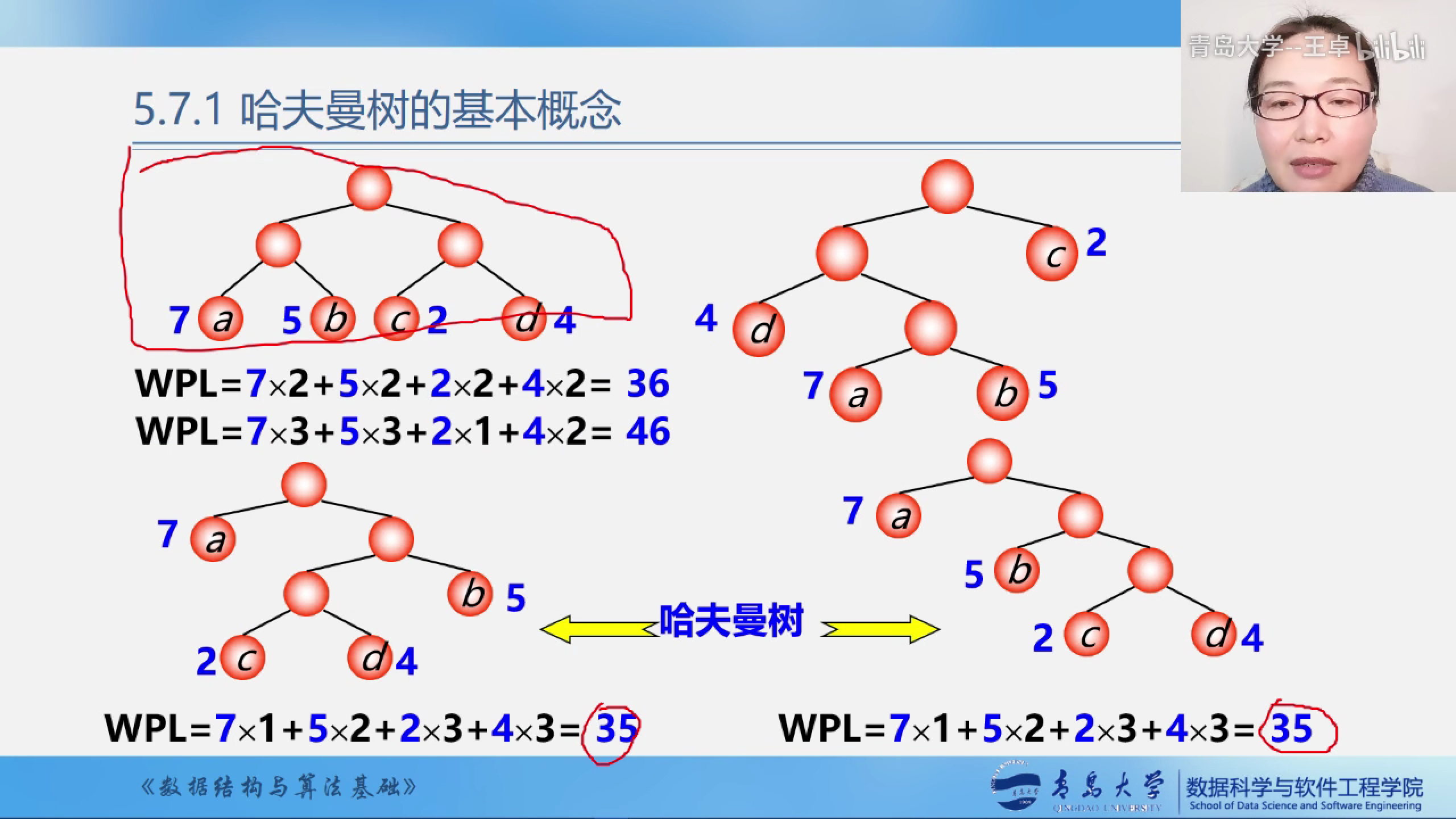
哈夫曼树
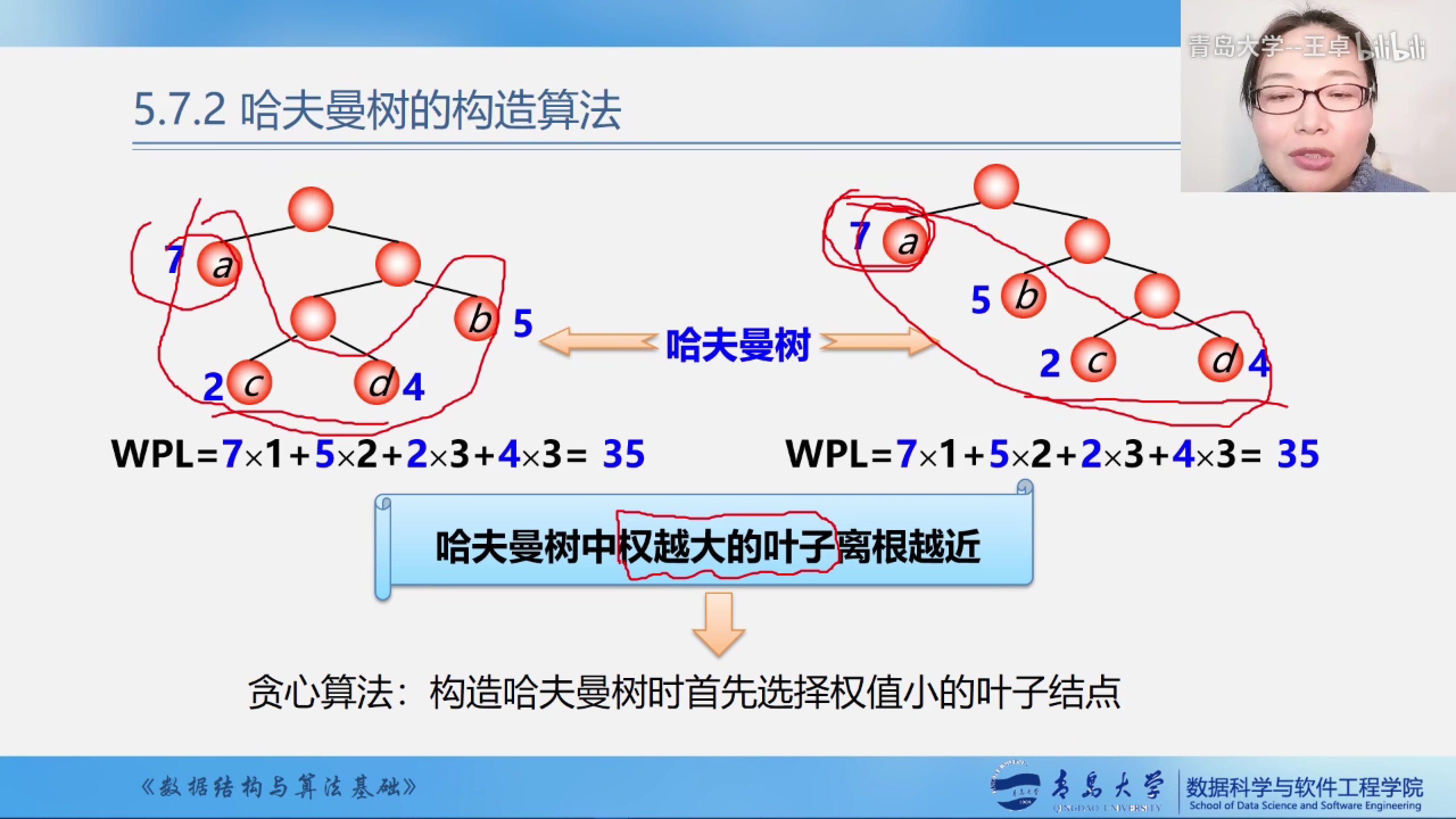
最优树:带权路径长度(WPL)最短的树.
注意:只有度相同才能比较.
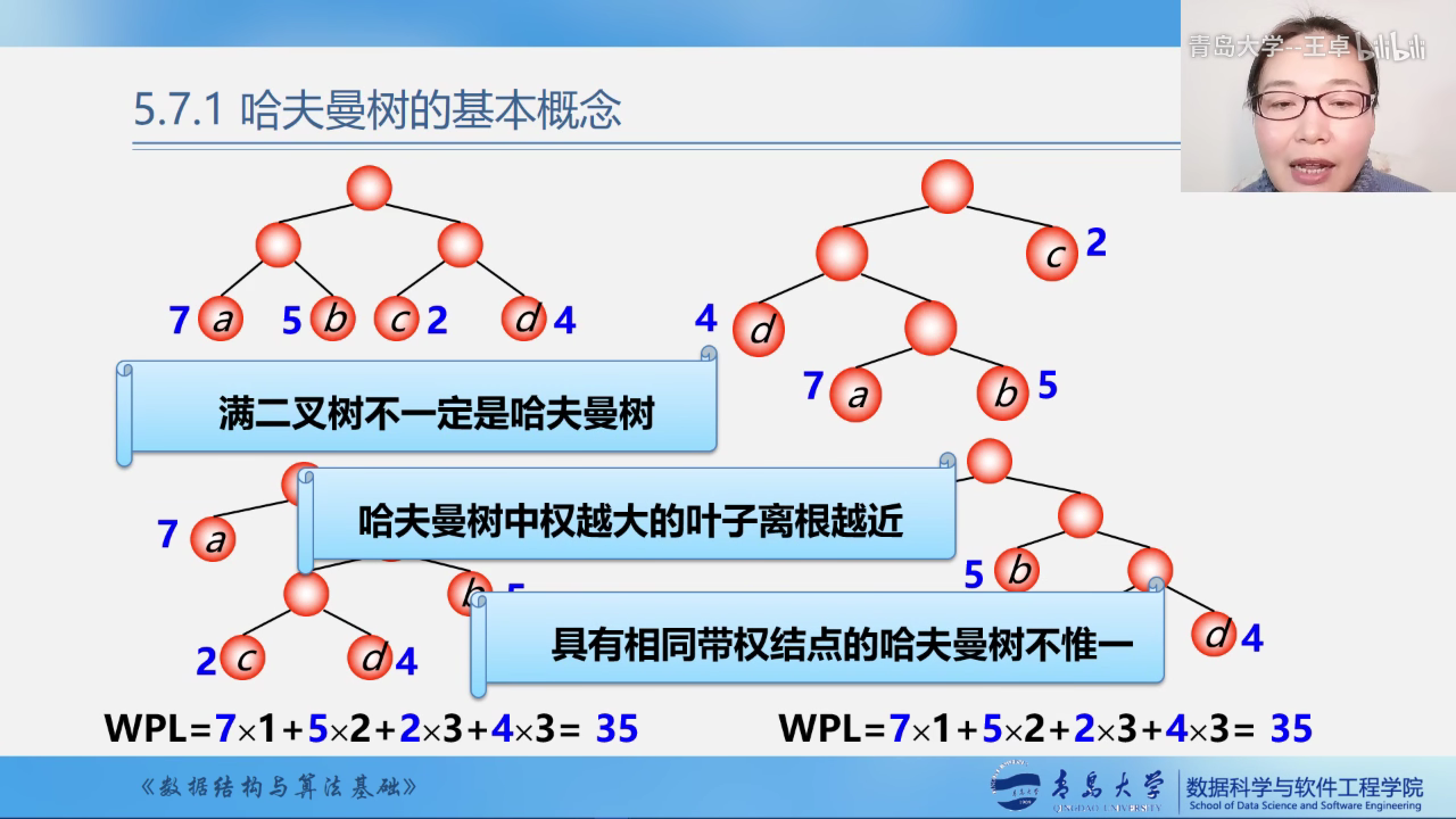
- 满二叉树不一定是哈夫曼树?
- 哈夫曼树重权越大的叶子结点离根越近
- 具有相同带权结点的哈夫曼树不唯一
构造哈夫曼树
贪心算法
构造哈夫曼树时首先选择权值小的叶子结点.
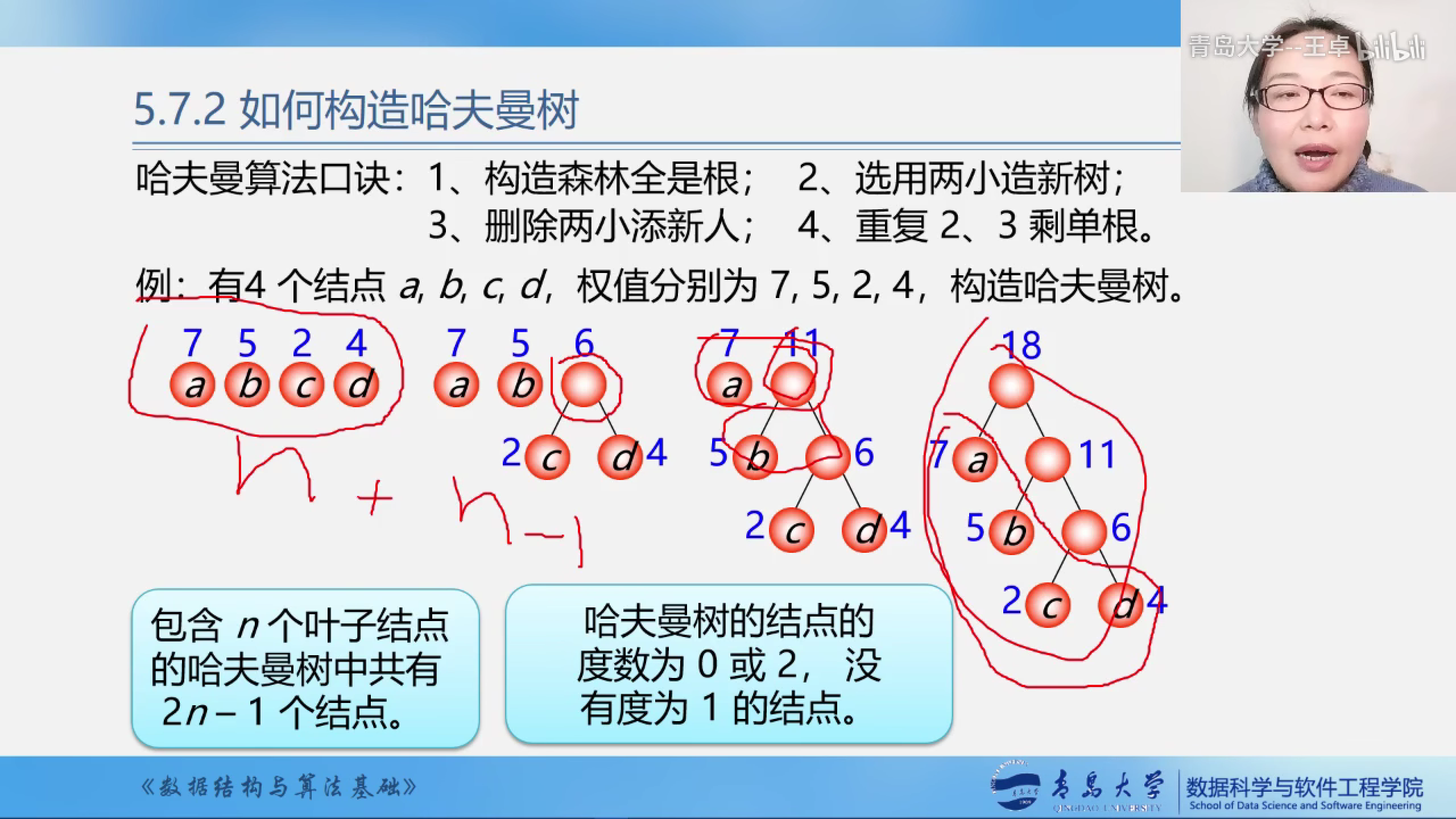
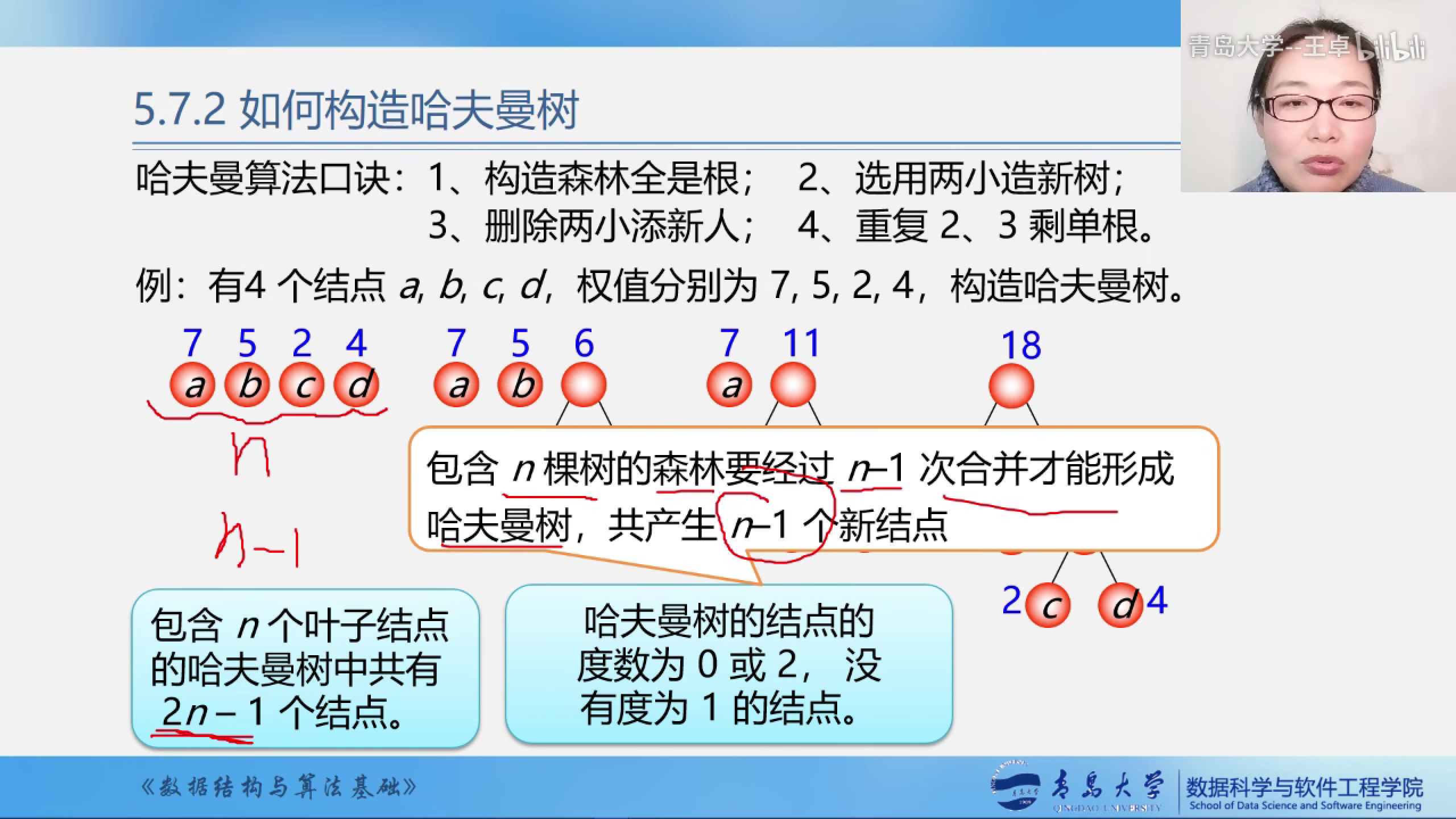
哈夫曼算法
- 构造森林全是根
- 选用两小造新树
- 删除两小添新人
- 重复2,3剩单根
这样就可以得到一个哈夫曼树.
哈夫曼树中只有度为2或者度为0的结点,没有读为1的结点
n个叶子结点的哈夫曼树共有2n-1个结点.
例2
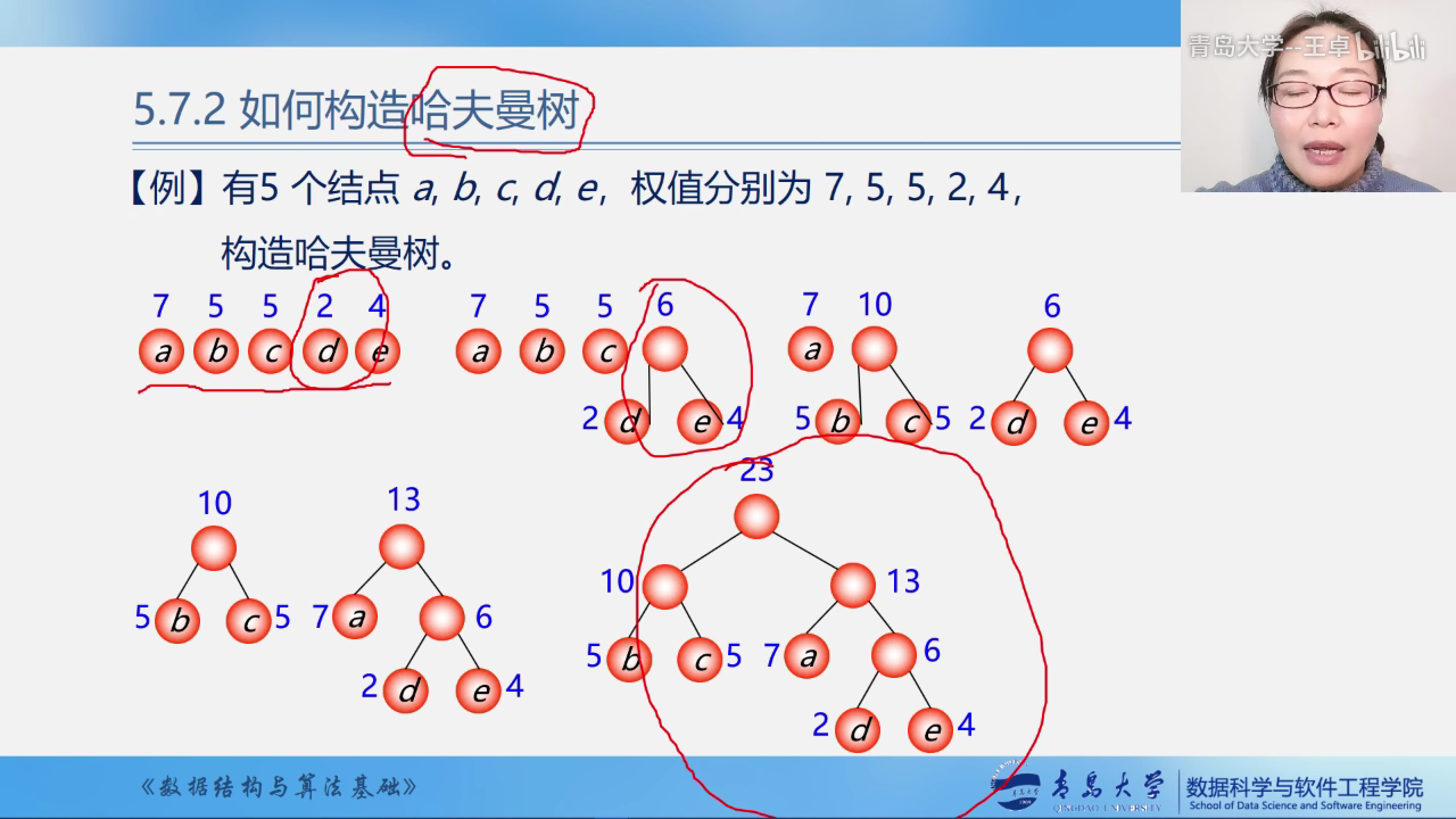
总结
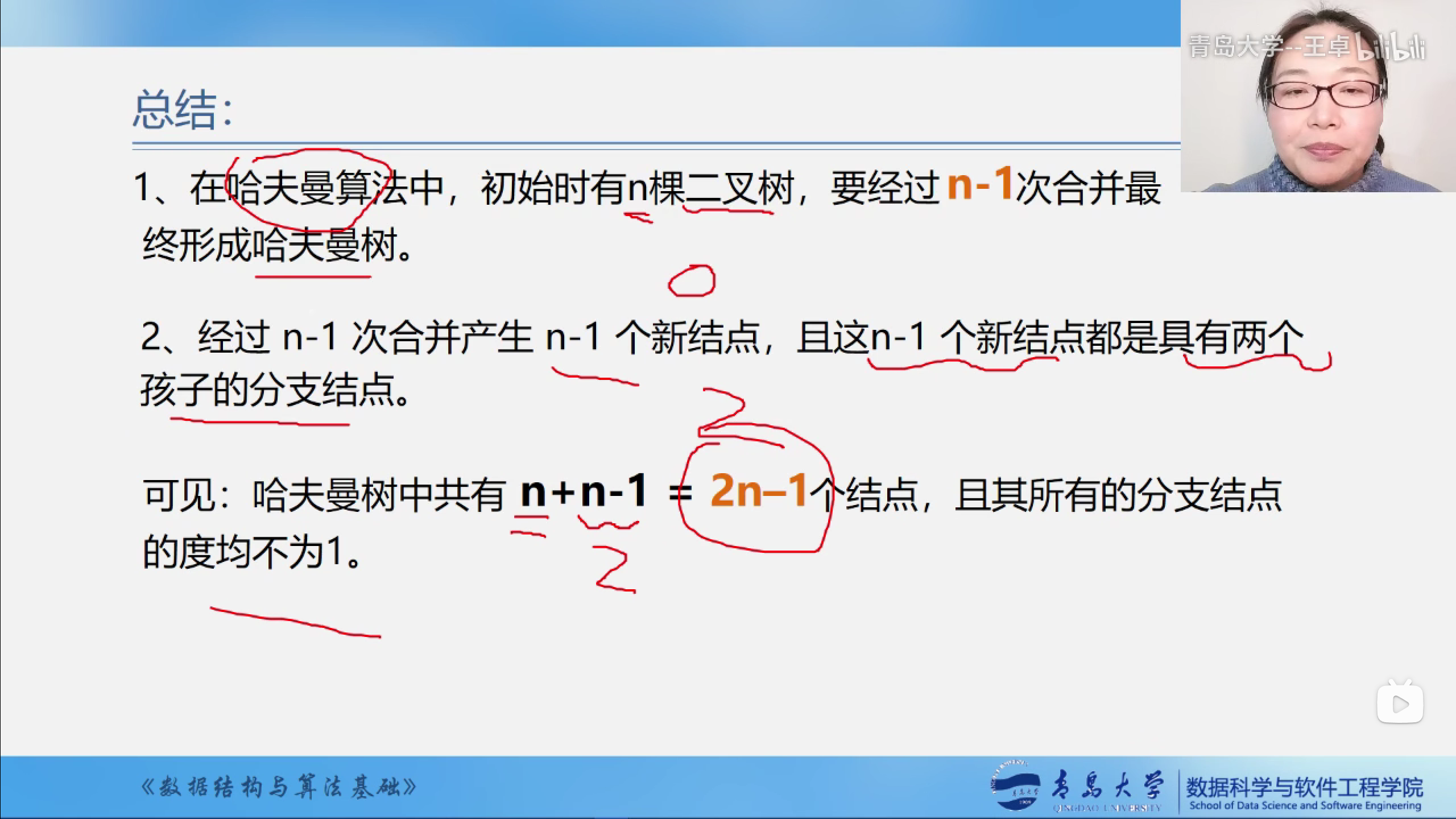
- n个结点通过n-1次合并最终形成哈夫曼树.
- 哈夫曼树中共有2n-1个结点
原本有n个结点,两两结合出现了n-1个新结点,同时因为这样两两结合的方式,产生的结点就没有度为1的结点.所以哈夫曼树共有2n-1个节点.
哈夫曼树的构造算法
一维结构数组
采用一维结构数组
需要2n-1个结点的数组,不适用0下标.
结点结构有三部分组成,分别是权值,双亲结点,左孩子结点和右孩子结点.
#include <bits/stdc++.h>
using namespace std;
typedef struct {
int weight;//树的权重
int parent;//树的双亲结点
int lch;//左孩子
int rch;//右孩子
} HTNode, *HuffmanTree;
int main () {
HuffmanTree H = NULL;
return 0;
}
- 构造森林全是根
- 选用两小造新树
- 删除两小添新人
- 重复2,3剩单根
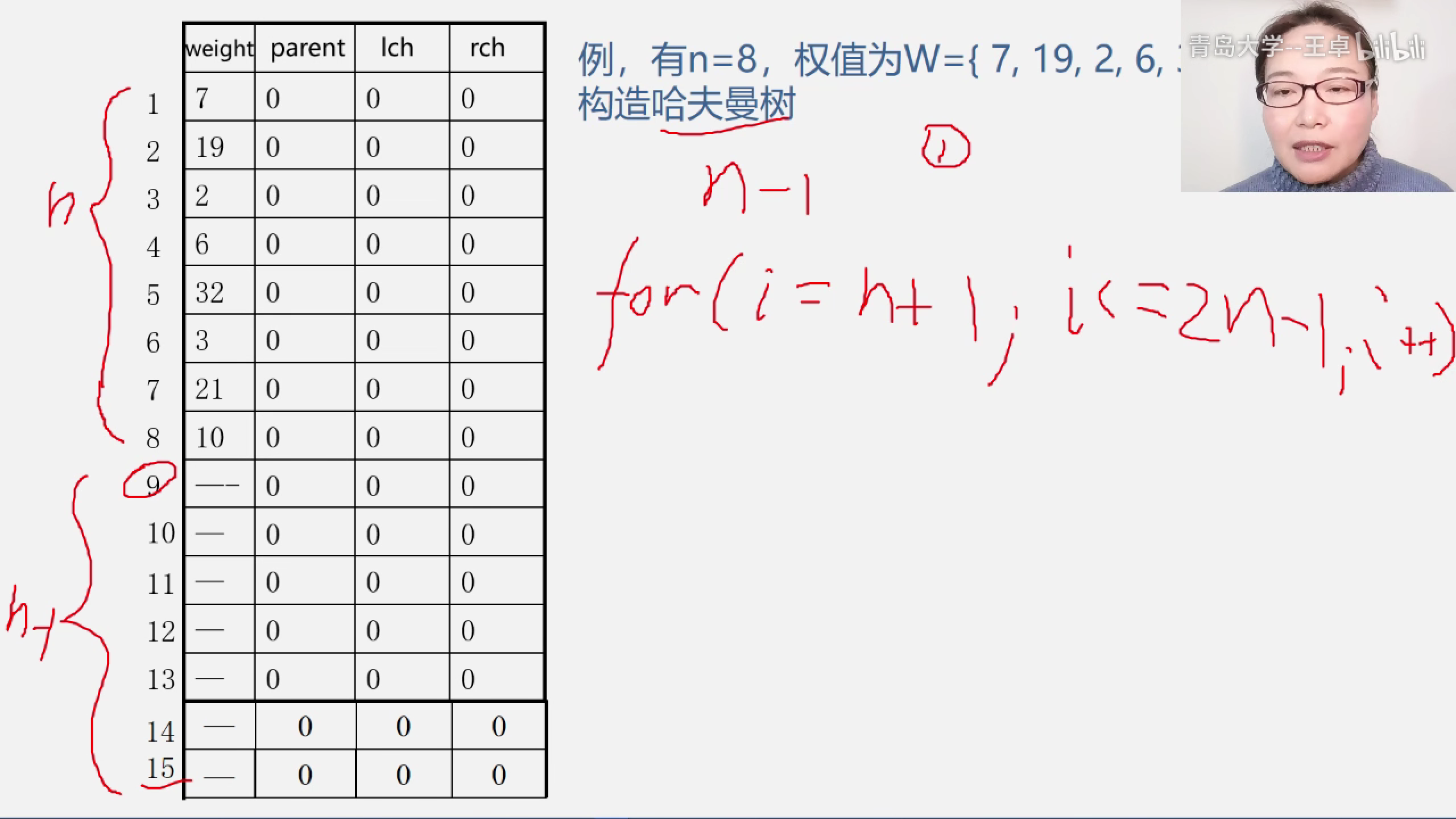
算法代码实现
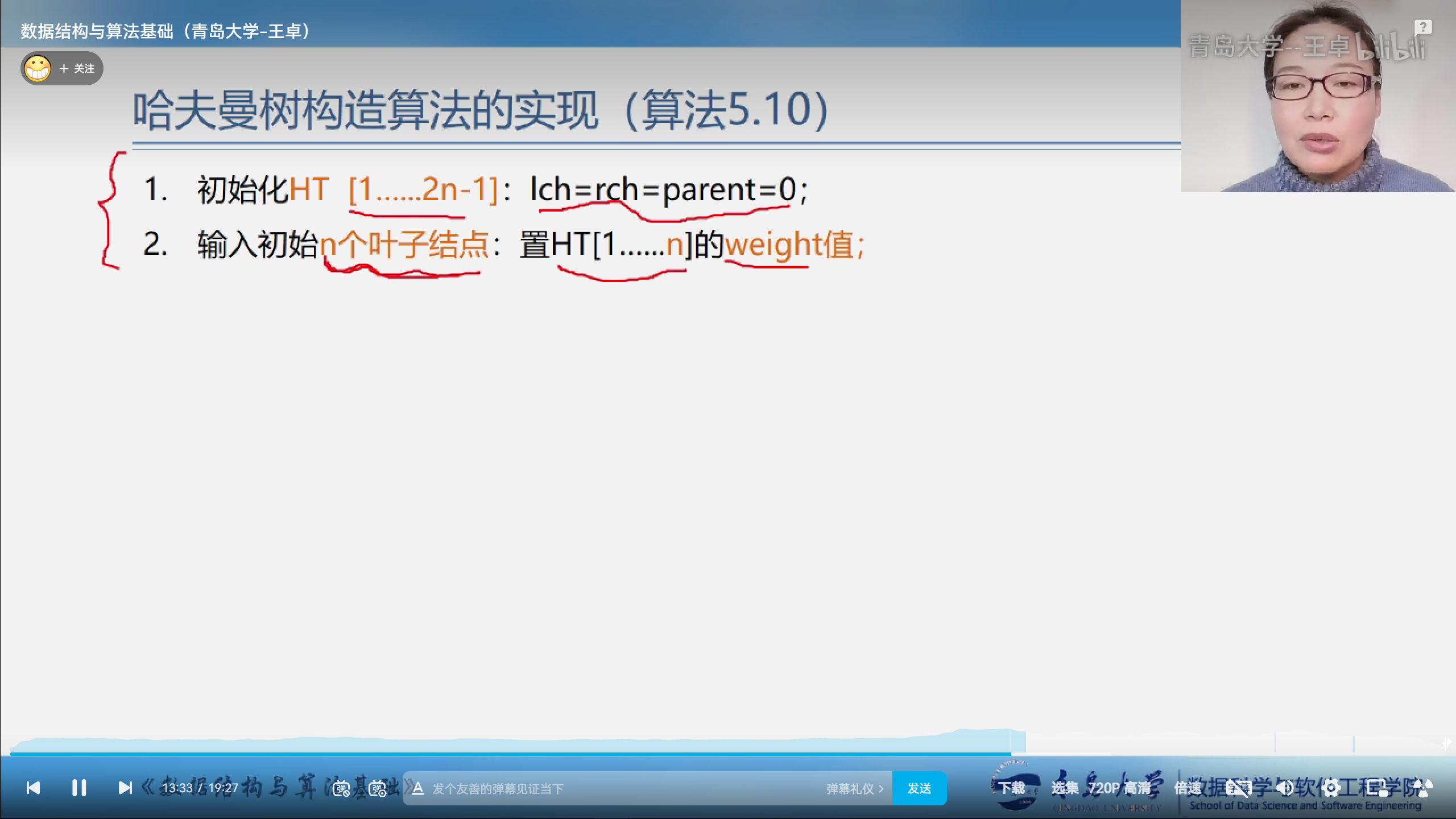
- 初始化 lch=rch=parent=0,这样的话每个结点都是孤立的一个结点.
- 输入初始n个叶子结点的weight值,需要放入权值进行贪心.
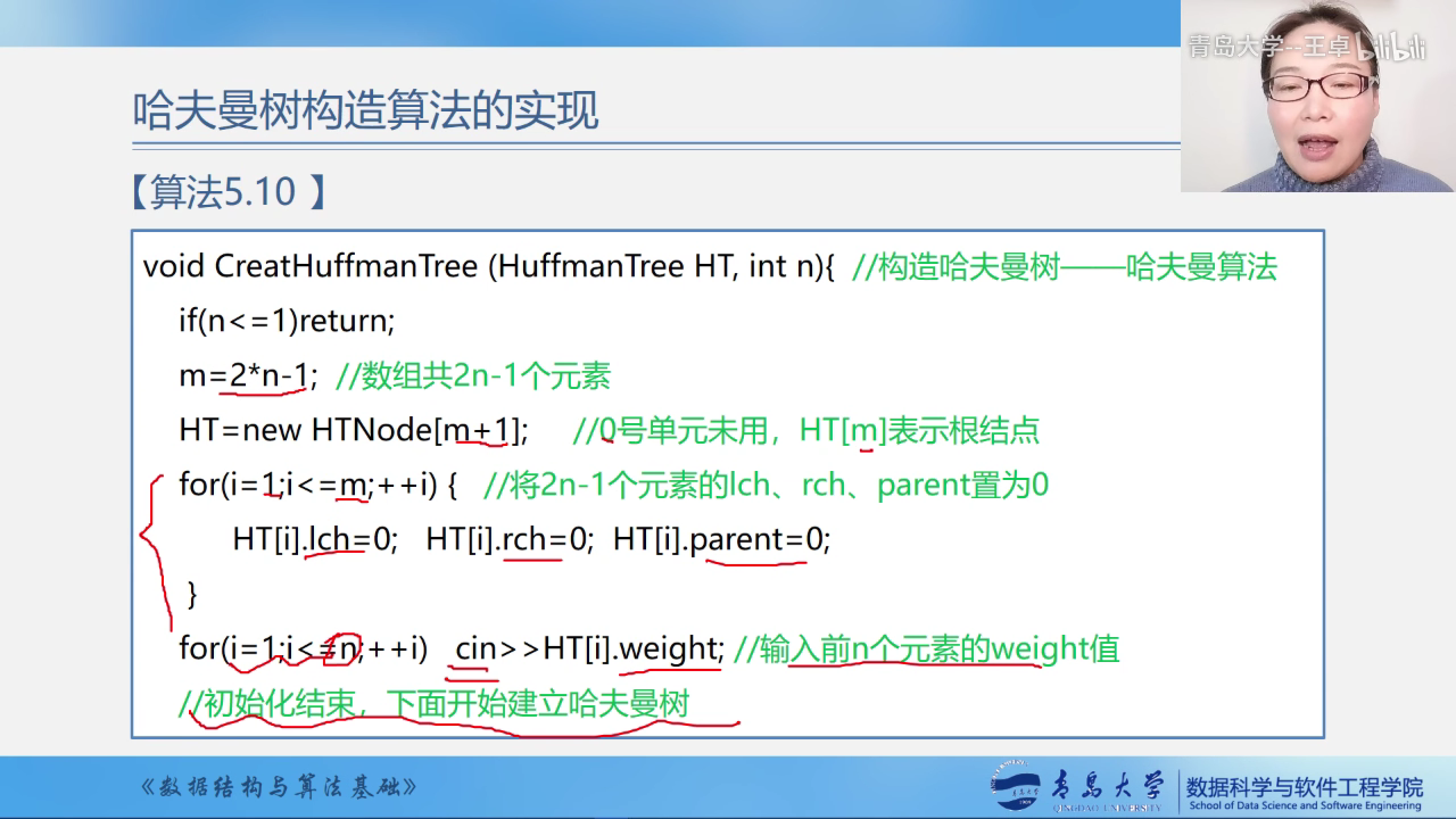
- 进行n-1次合并
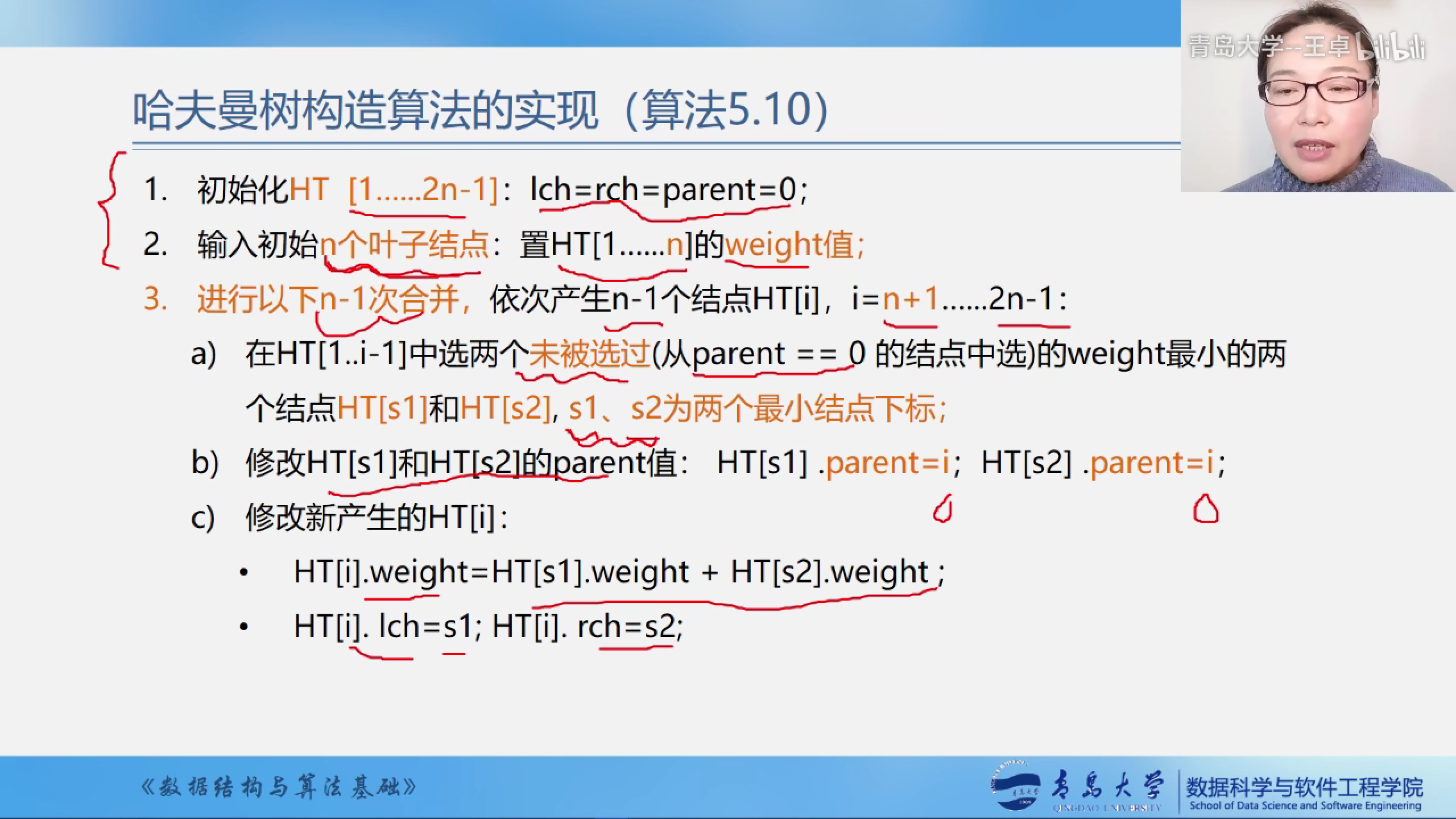
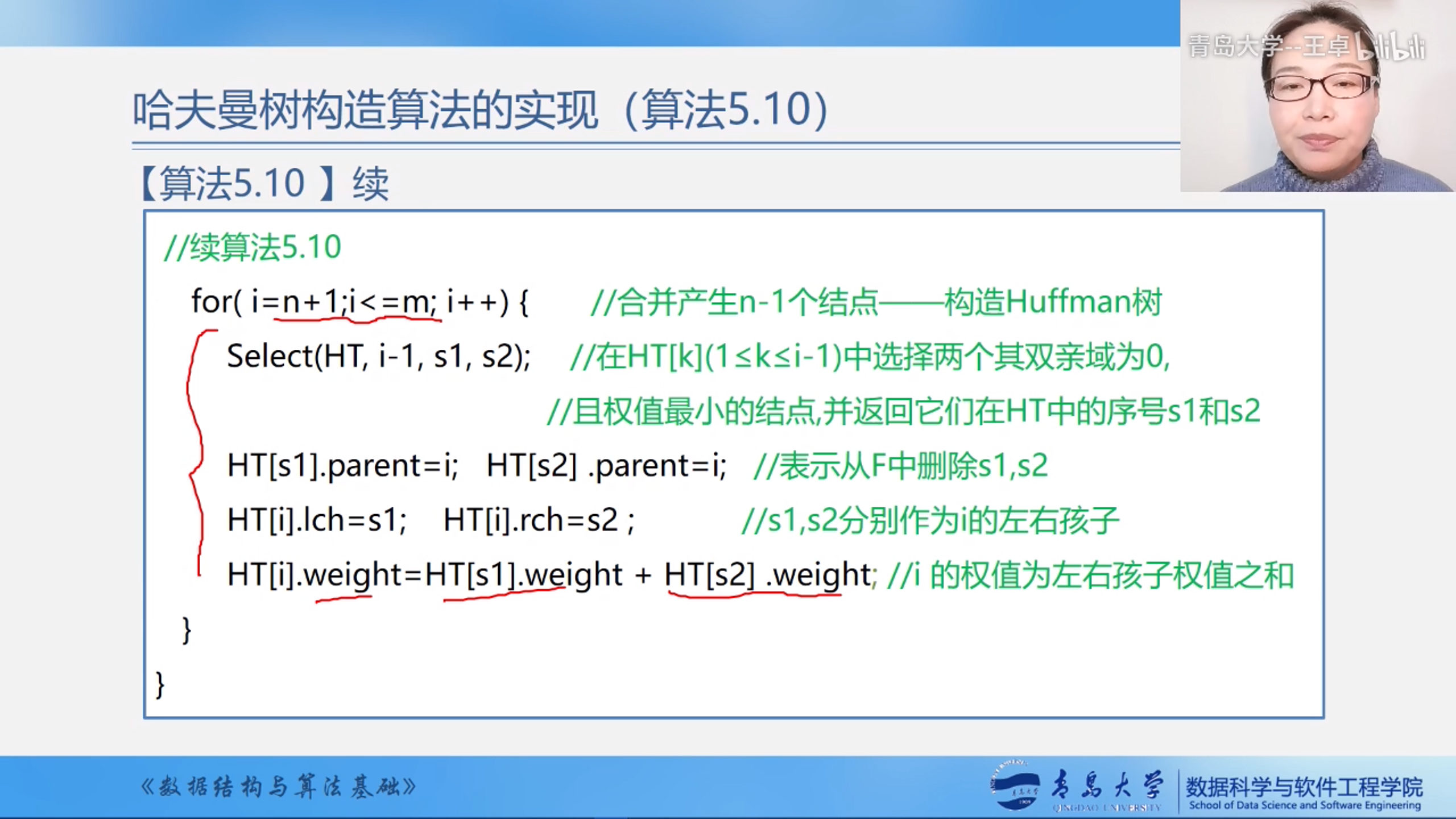
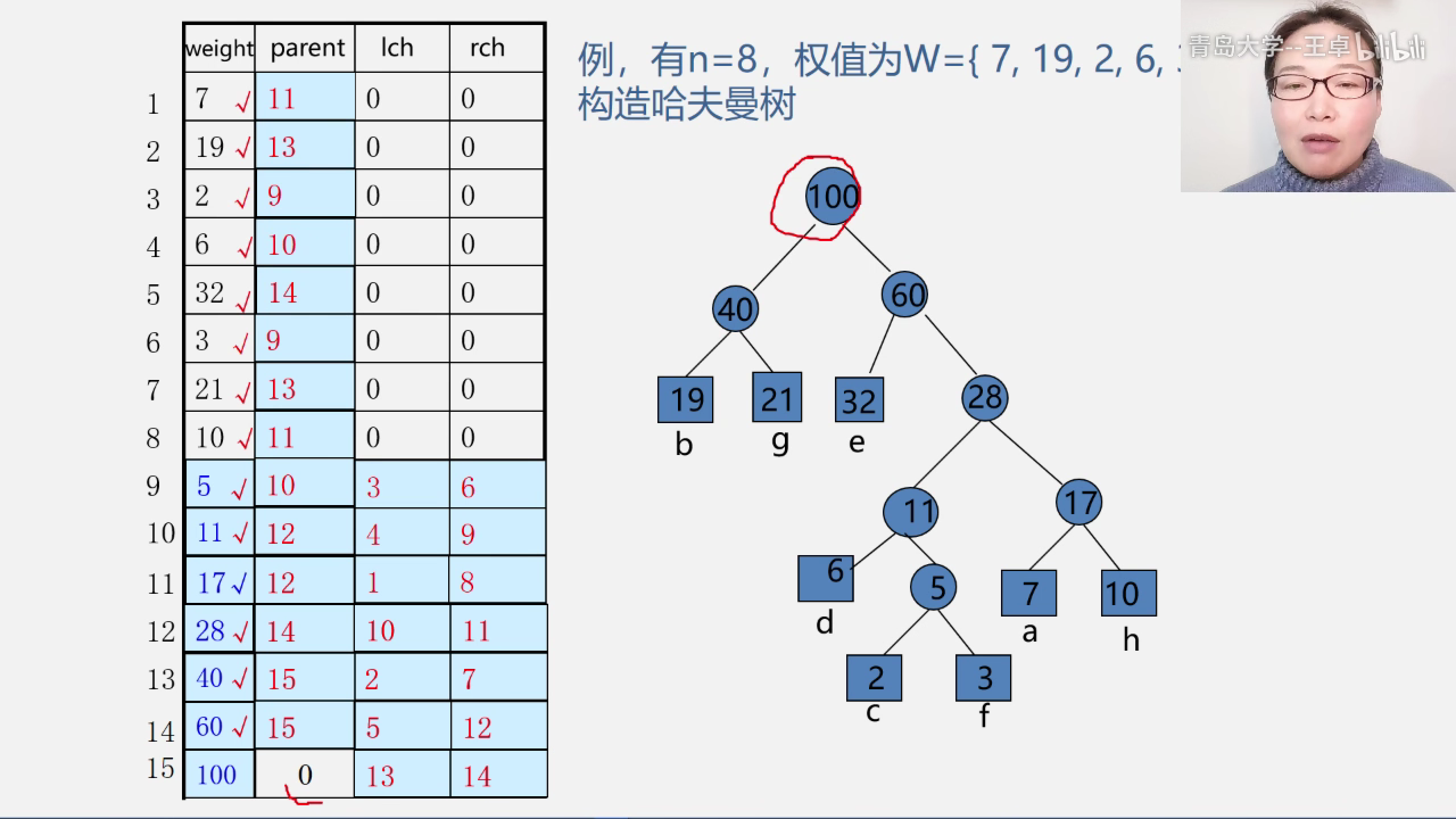
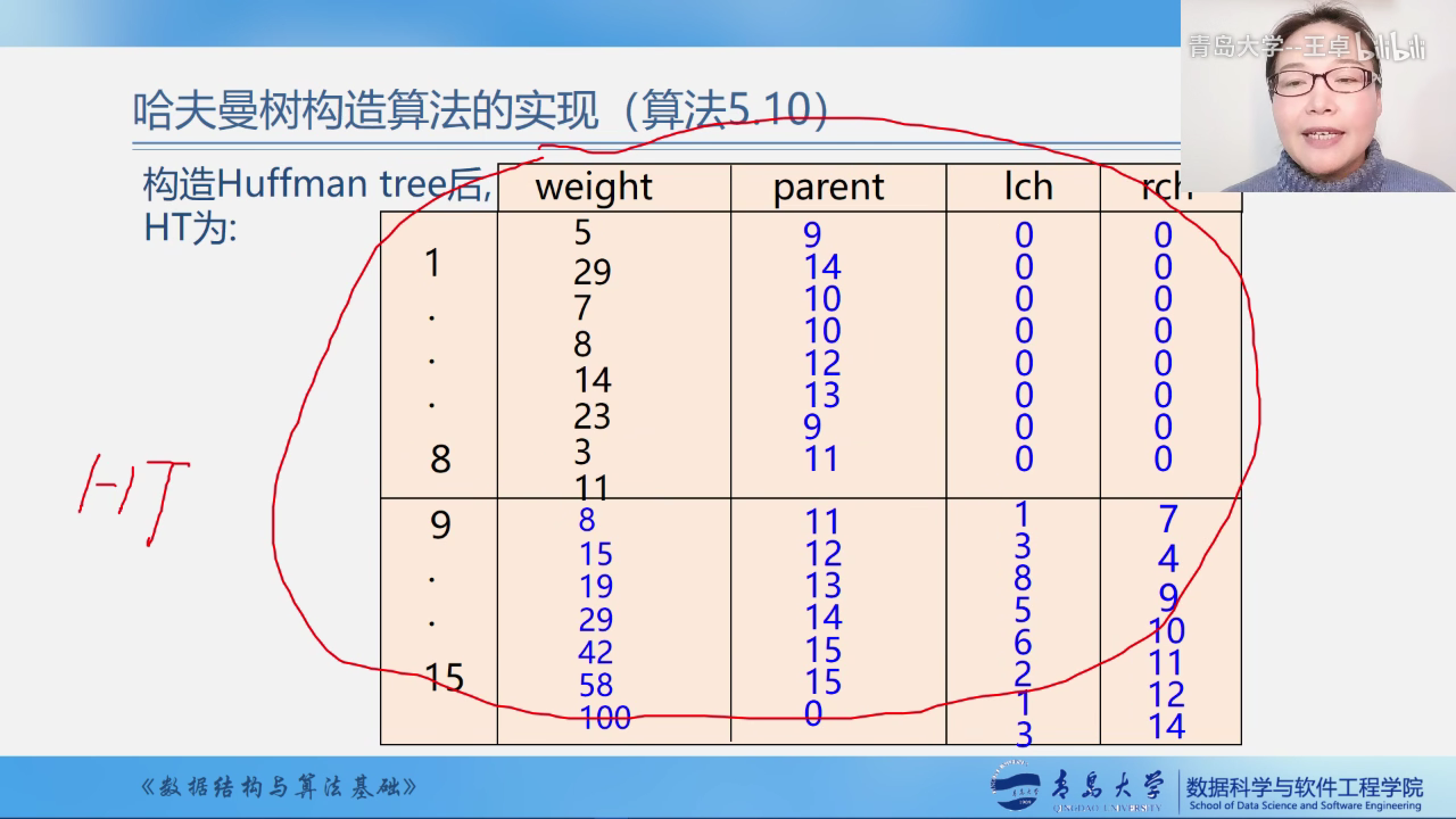
例子
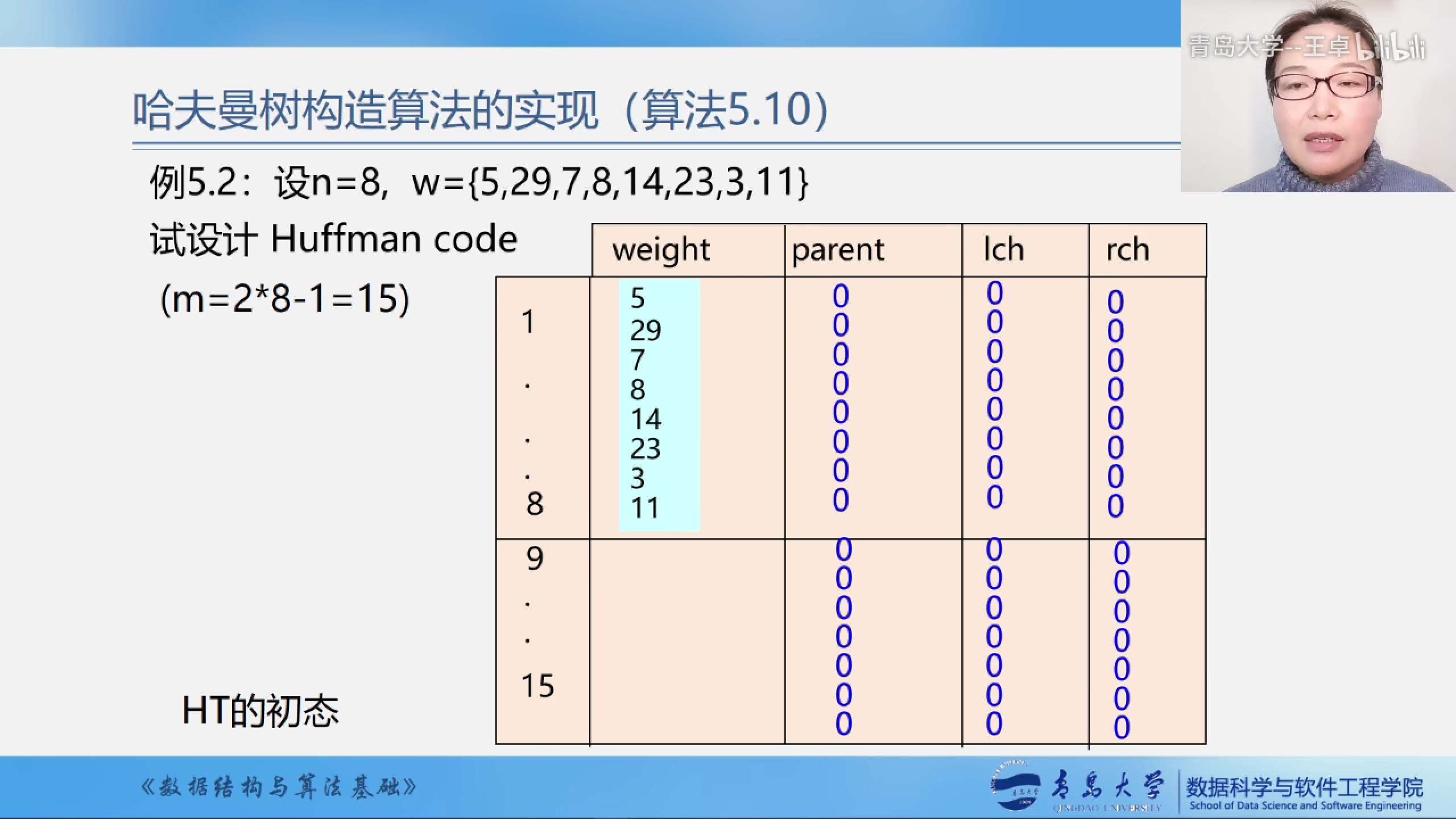
数组构造好二叉树之后的样子
#include <bits/stdc++.h>
using namespace std;
typedef struct {//哈夫曼树的结点结构
int weight;
int parent;
int lch;
int rch;
} HTNode, *HuffamnTree;
/*
该函数用来挑选出两个最小值的下标
*/
void Select(HuffamnTree HT, int length, int &s1, int &s2) {
/*
先假定数组的前两位中的较小的是最小，较大的是次小
循环检查其余的元素，
若新元素小于最小，则，最小变为次小，新元素成为最小
否则，再判断新元素是否小于次小，是，则新元素变为次小
循环结束，输出两个数。
*/
int s1_min = 99999999;
int s2_min = 99999999;
for (int i = 1; i <= length; i++) {
if (HT[i].parent == 0) {
if (HT[i].weight < s1_min) {
s2_min = s1_min;
s1_min = HT[i].weight;
} else if (HT[i].weight < s2_min) {
s2_min = HT[i].weight;
}
}
}
//该循环找到了这个数组中的最小的权重,并且保证下来
for (int i = 1; i <= length; i++) {
if (HT[i].parent == 0) {
if (HT[i].weight == s1_min) {
s1 = i;
}
}
}//该函数用来找到s1的下标
for (int i = 1; i <= length; i++) {
if (HT[i].parent == 0) {
if (HT[i].weight == s2_min && i != s1) {//万一s1和s2相同,特殊判断一下
s2 = i;
}
}
}
// cout << "两个最小值" << '\n';
// cout << s1_min << ' ' << s2_min << '\n';
// cout << "两个最大的id" << '\n';
// cout << s1 << ' ' << s2 << '\n';
}
/*
该函数用来构造哈夫曼树,需要哈夫曼数组的地址
*/
void CreateHuffmanTree(HuffamnTree &HT, int n) {
if (n <= 1) {
return;
}
int m = 2 * n - 1;//原本有n个数据但是要使用2*n-1个数组
HT = new HTNode[m + 1]; //构造一个0---2n-1的数组,0号位置不用,多构造一位从下标1开始
for (int i = 1; i <= m; i++) {//全部进行初始化
HT[i].lch = 0;
HT[i].rch = 0;
HT[i].parent = 0; //初始化代码
}
for (int i = 1; i <= n; i++) {
cin >> HT[i].weight; //读入每个结点的权值
}
//从第n+1个结点开始构造,一直到第m个结点
for (int i = n + 1; i <= m; i++) {
int s1 = 0, s2 = 0;//s1,s2保存前i-1个结点的最小的两个结点的下标
Select(HT, i - 1, s1, s2);//挑选前i-1个结点的最小的两个结点的下标
HT[s1].parent = i;
HT[s2].parent = i;//让这两个结点的双亲指向i;
HT[i].lch = s1;
HT[i].rch = s2;//让第i个结点的左孩子右孩子指向s1和s2
HT[i].weight = HT[s1].weight + HT[s2].weight;//当前结点的权重为两个结点的权重之和
// printf("%d %d\n", s1, s2);
// printf("%d %d\n", HT[s1].weight, HT[s2].weight);
// printf("序号=%d weight=%d parent=%d lch=%d rch=%d\n", i, HT[i].weight, HT[i].parent, HT[i].lch, HT[i].rch);
}
}
/*
遍历哈夫曼树的函数
*/
void print(HuffamnTree HT, int n) {
for (int i = 1; i <= 2 * n - 1; i++) {
printf("序号=%d weight=%d parent=%d lch=%d rch=%d\n", i, HT[i].weight, HT[i].parent, HT[i].lch, HT[i].rch);
}
}
int main () {
HuffamnTree HT = NULL;
CreateHuffmanTree(HT, 8);
cout << HT << '\n';
print(HT, 8);
/*
测试样例
7 19 2 6 32 3 21 10
5 29 7 8 14 23 3 11
*/
return 0;
}
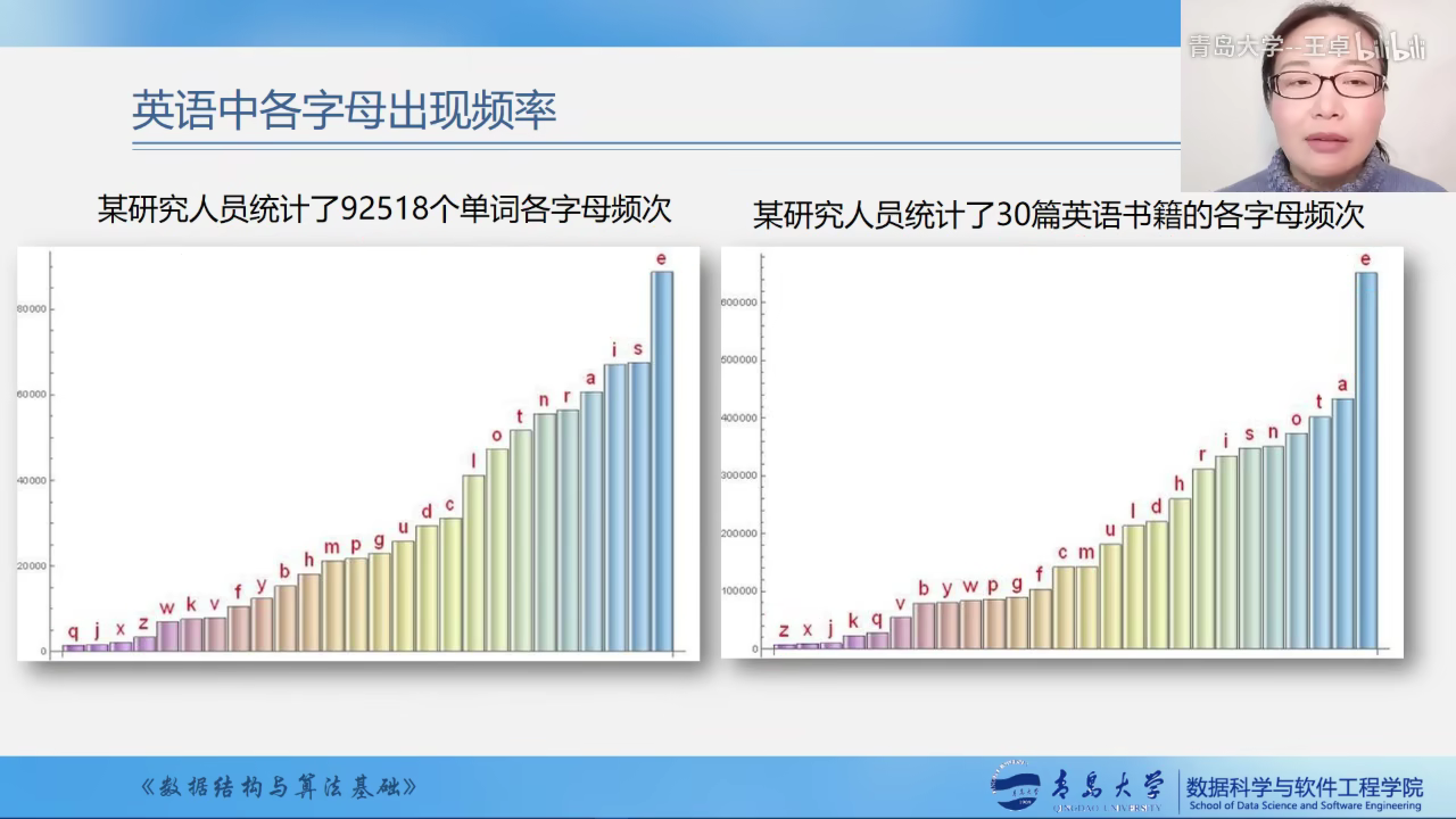
哈夫曼编码
为什么使用哈夫曼编码?
让出现次数较多的字符采用进可能短的编码.
同时使用次数越多的字母,编码越短,使用次数少的字母编码越长
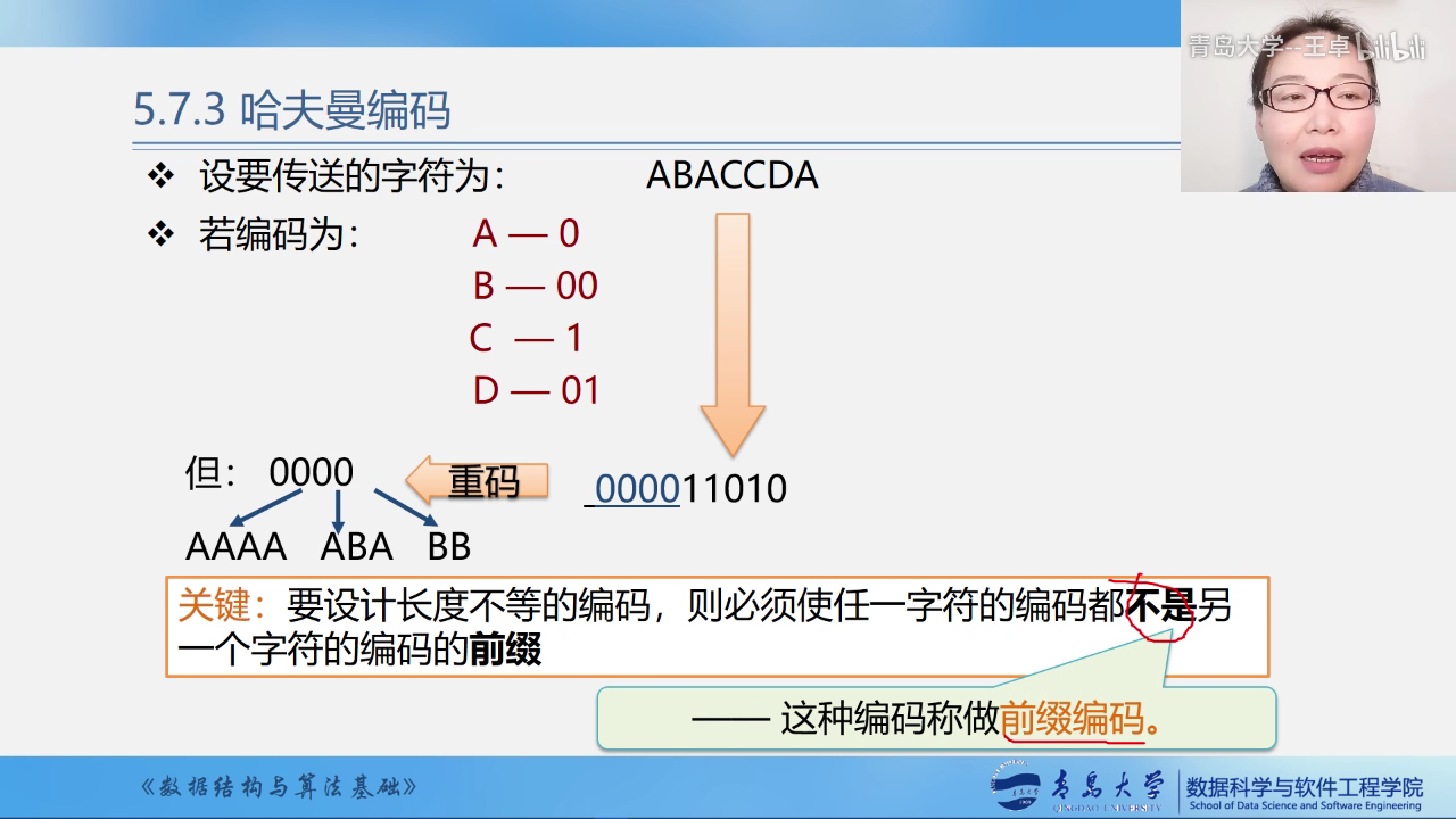
不能出现重码
要设计任一字符的编码都不是另一个字符的编码的前缀.否则就会重复.
这样的编码叫做前缀编码.
采用哈夫曼编码
可以有效的解决上面的问题
例题
为什么哈夫曼编码是前缀编码?
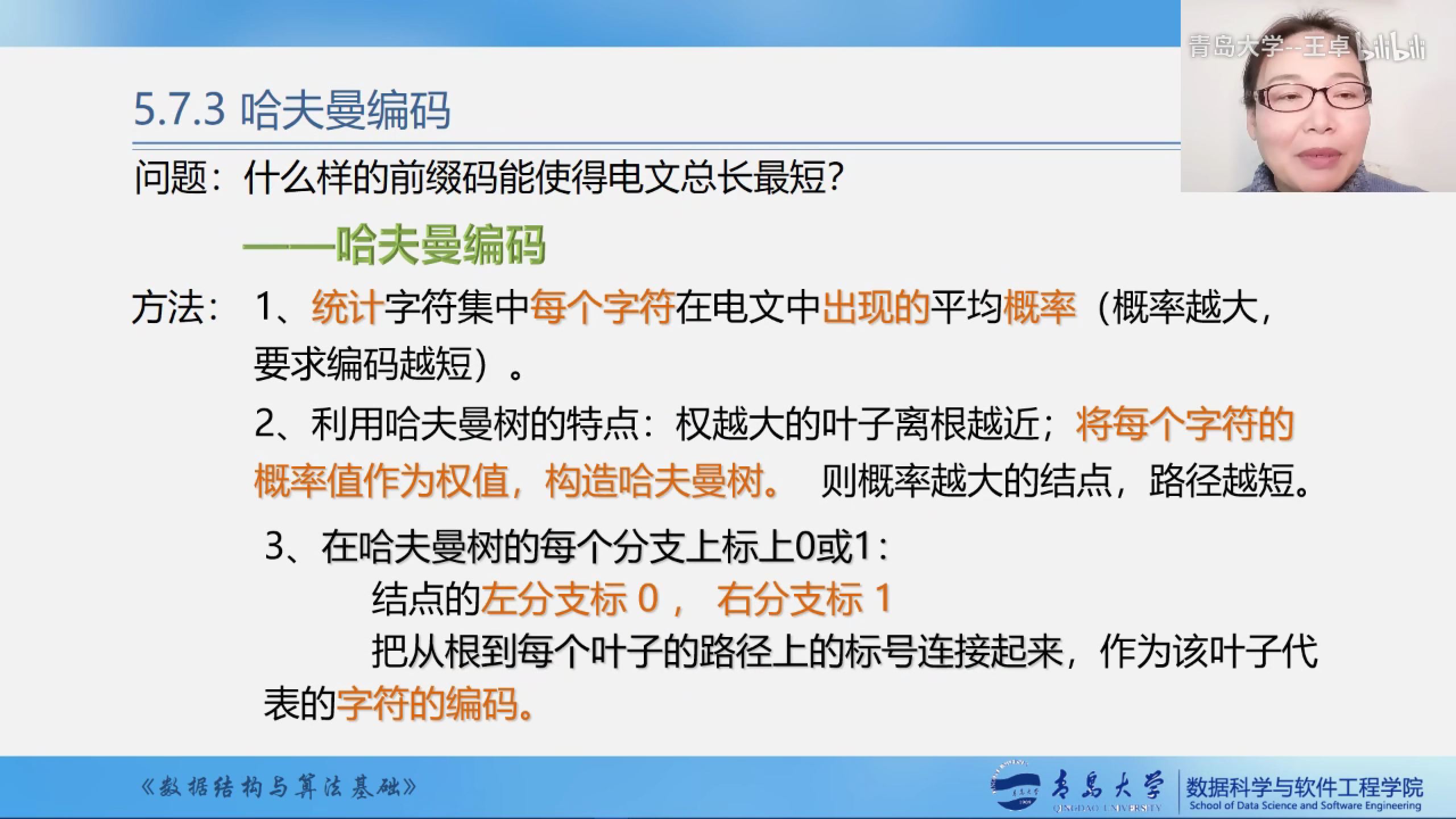
为什么哈夫曼编码能保证字符编码总长最短?
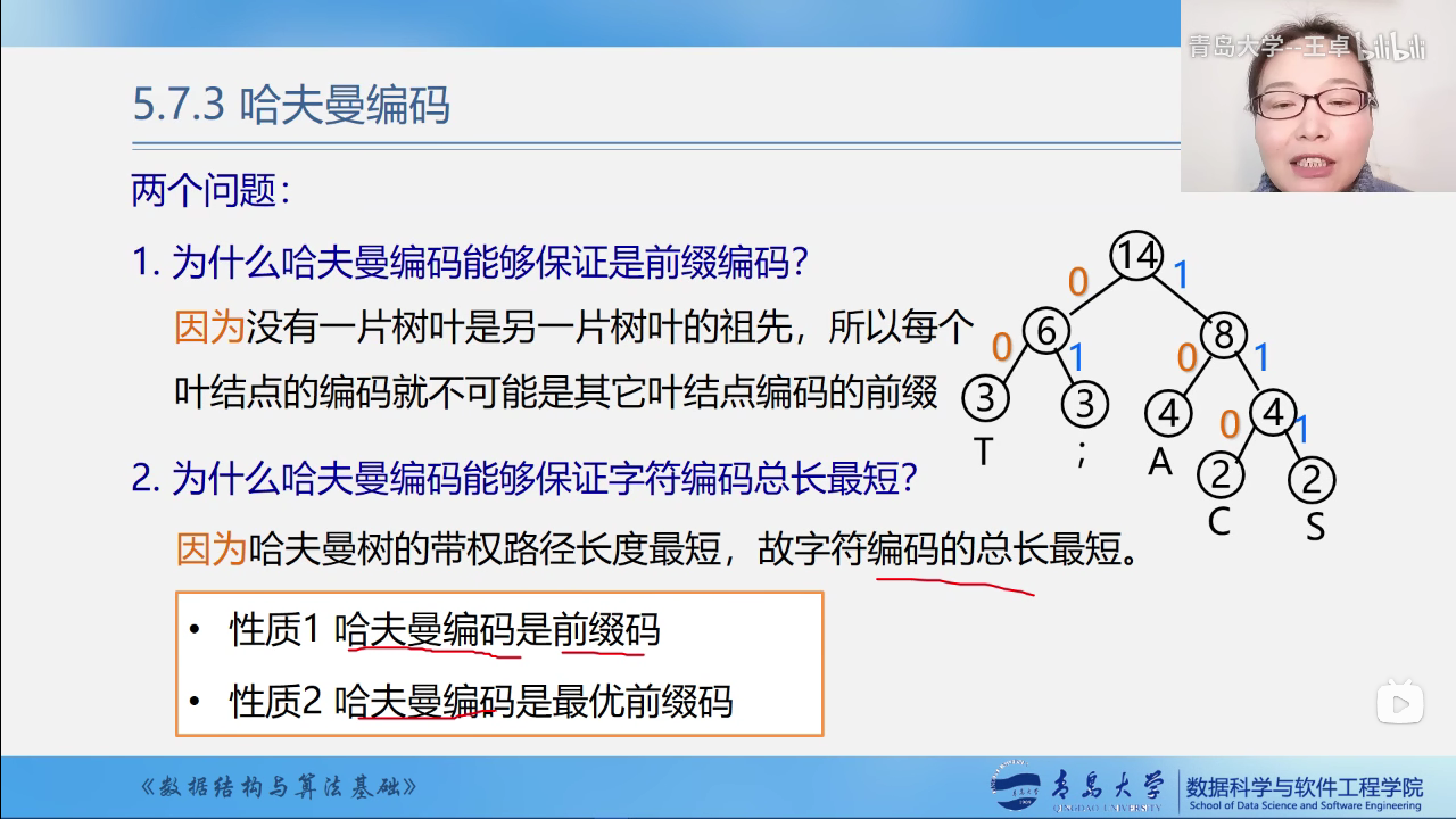
- 哈夫曼编码是前缀码
- 哈夫曼编码是最优前缀码
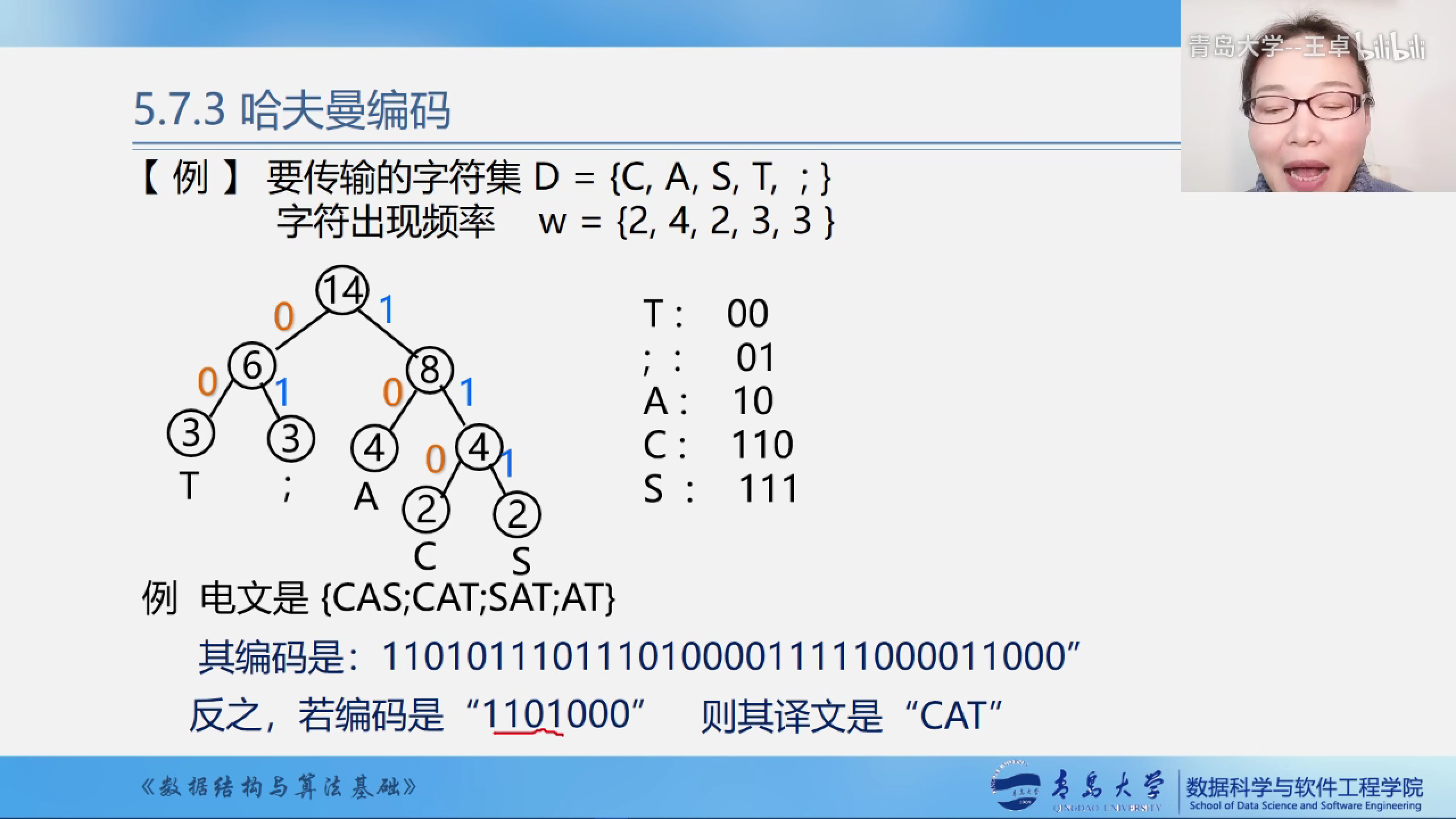
例题
例题中的哈夫曼树
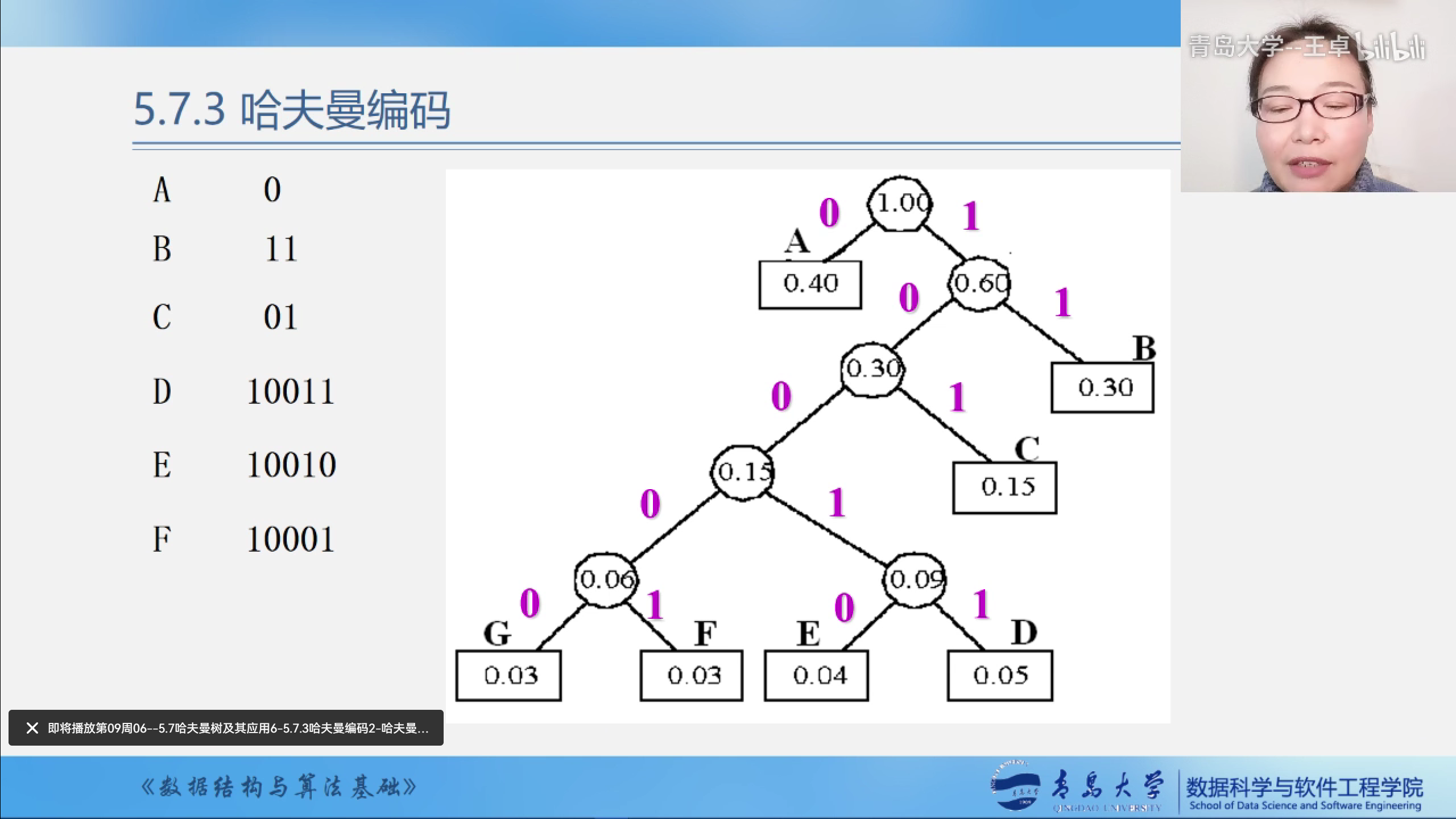
哈夫曼编码的实现过程
为了更加的方便我们使用了C++中的string对算法进行了具体实现
#include <bits/stdc++.h>
#include<windows.h>
#define yes cout<<"YES"<<'\n'
#define no cout<<"NO"<<'\n'
using namespace std;
typedef pair<int, int> PII;
const int N = 100008;
typedef struct {//哈夫曼树的结构体
double weight;//权重
int parent;
int lch;
int rch;
} HTNode, *HuffmanTree;
/*
创建哈夫曼树的函数
n为元素个数
*/
void Select(HuffmanTree HT, int length, int &s1, int &s2) {
// 先假定数组的前两位中的较小的是最小，较大的是次小
// 循环检查其余的元素，
// 若新元素小于最小，则，最小变为次小，新元素成为最小
// 否则，再判断新元素是否小于次小，是，则新元素变为次小
// 循环结束，输出两个数。
double s1_min = 0x3f3f3f3f;
double s2_min = 0x3f3f3f3f; //赋值为极大值
for (int i = 1; i <= length; i++) {
if (HT[i].parent == 0) {
if (HT[i].weight < s1_min) {
s2_min = s1_min;
s1_min = HT[i].weight;
} else if (HT[i].weight < s2_min) {
s2_min = HT[i].weight;
}
}
}
//先找到最小值下面开始找下标
for (int i = 1; i <= length; i++) {
if (HT[i].parent == 0) {
if (HT[i].weight == s1_min) {
s1 = i; //找到第一个
}
}
}
for (int i = 1; i <= length; i++) {
if (HT[i].parent == 0) {
if (HT[i].weight == s2_min && i != s1) { //避免s1_min和s2_min出现bug
s2 = i;
}
}
}
}
void CreatHuffman(HuffmanTree &HT, int n) {
if (n <= 1) {
return;
}
int m = 2 * n - 1;
HT = new HTNode[m + 1]; //下标0不用
for (int i = 1; i <= m; i++) { //初始化哈夫曼树
HT[i].lch = 0;
HT[i].rch = 0;
HT[i].parent = 0;
}
//初始化结束
for (int i = 1; i <= n; i++) {
cin >> HT[i].weight; //读入权值
}
//下面构建哈夫曼树
for (int i = n + 1; i <= m; i++) {
int s1 = 0, s2 = 0;
Select(HT, i - 1, s1, s2);
HT[s1].parent = i;
HT[s2].parent = i; //让s1,s2指向现在的双亲
HT[i].lch = s1;
HT[i].rch = s2; //第i个节点保存左孩子右孩子
HT[i].weight = HT[s1].weight + HT[s2].weight;
}
}
//void traverse(HuffmanTree HT, int n) {
// for (int i = 1; i <= 2 * n - 1; i++) {
// printf("序号=%d weight=%d parent=%d lch=%d rch=%d\n", i, HT[i].weight, HT[i].parent, HT[i].lch, HT[i].rch);
// }
//
//}
void HuffmanCode(HuffmanTree HT, string HC[], int n) {
for (int i = 1; i <= n; i++) {
int f = HT[i].parent;
int c = i;
while (f != 0) {
if (HT[f].lch == c) {
HC[i] = HC[i] + '0';
} else {
HC[i] = HC[i] + '1';
}
c = f;//将c赋值为当前的f
f = HT[f].parent;//f为当前f的双亲
}
reverse(HC[i].begin(), HC[i].end());
}
}
int main () {
int n;
printf("请输入你要进行编码的字符的数量\n");
cin >> n;
HuffmanTree HT = NULL;
printf("下面请您输入每个字符对应的权重\n");
CreatHuffman(HT, n);
// traverse(HT, 8);
string HC[10000];
HuffmanCode(HT, HC, n);
printf("下面是生成的哈夫曼编码\n");
for (int i = 1; i <= n; i++) {
cout << HC[i] << '\n';
}
Sleep(5000);
return 0;
}
文件的编码和译码
使用ascii码来编码
使用哈夫曼编码
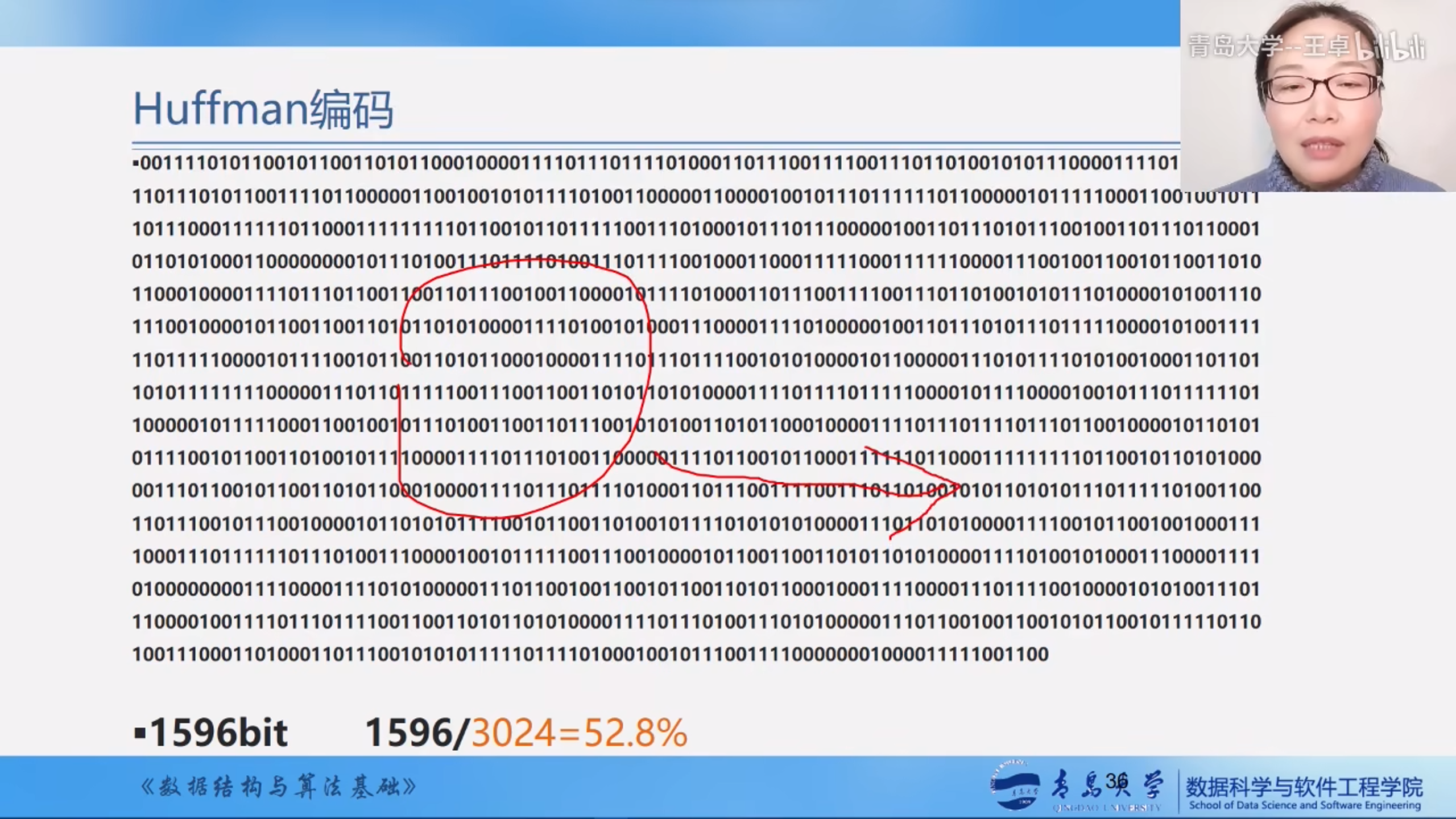
编码
-
输入各字符及其权值
-
构造哈夫曼树--HT[i]
-
进行哈夫曼编码--HC[I]
-
查询HC[i],得到各字符串的哈夫曼编码
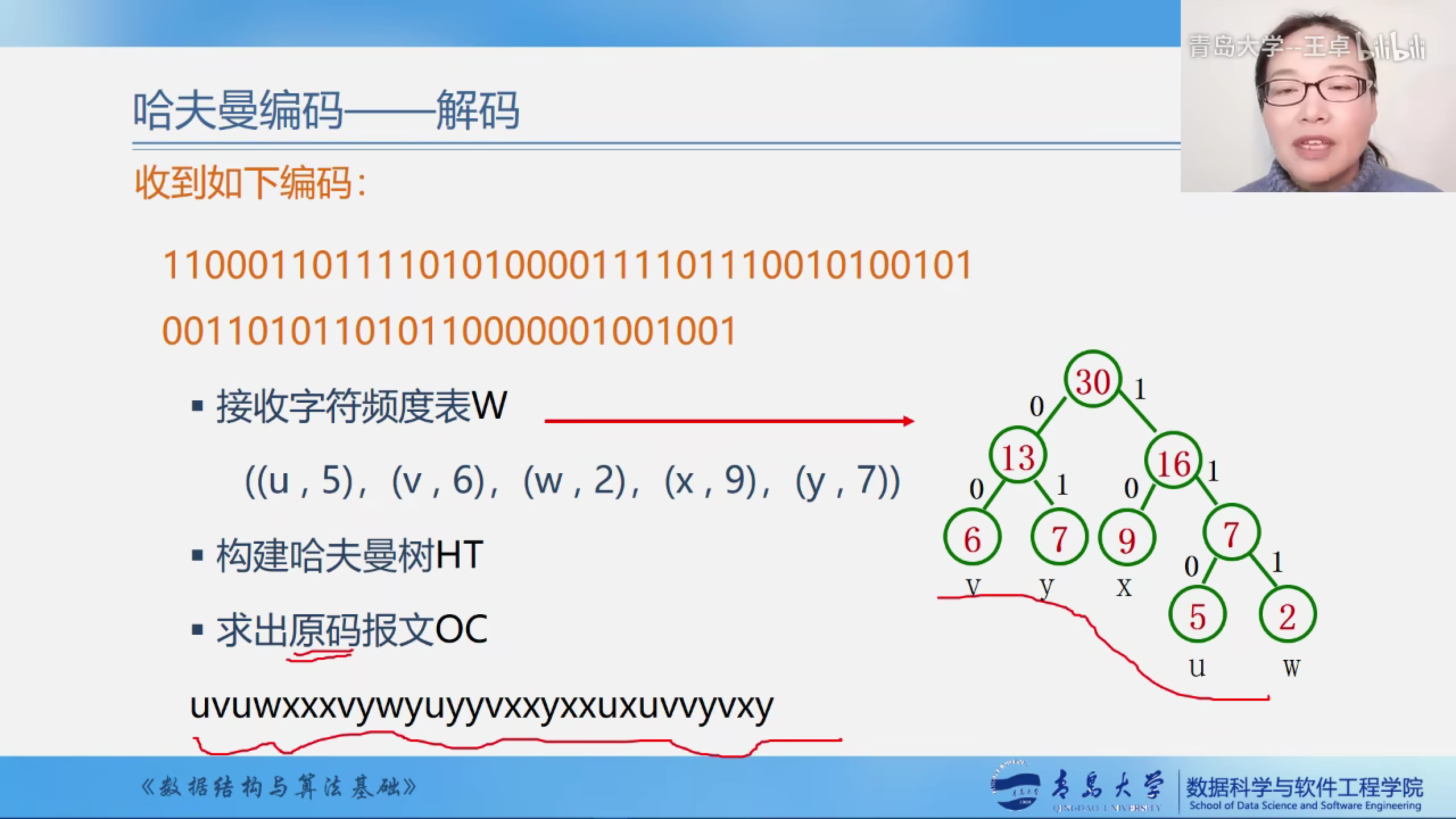
解码
- 构造哈夫曼树
- 依次读入二进制码
- 读入0,则走左孩子;读入1,则走右孩子
- 一旦到达叶子结点时,即可翻译出字符
- 然后再从根出发继续译码,指导结束
按照字符频度表w构建哈夫曼树,求出原码报文OC
