二叉树的存储结构和操作算法
二叉树的存储结构和操作算法
二叉树的存储结构
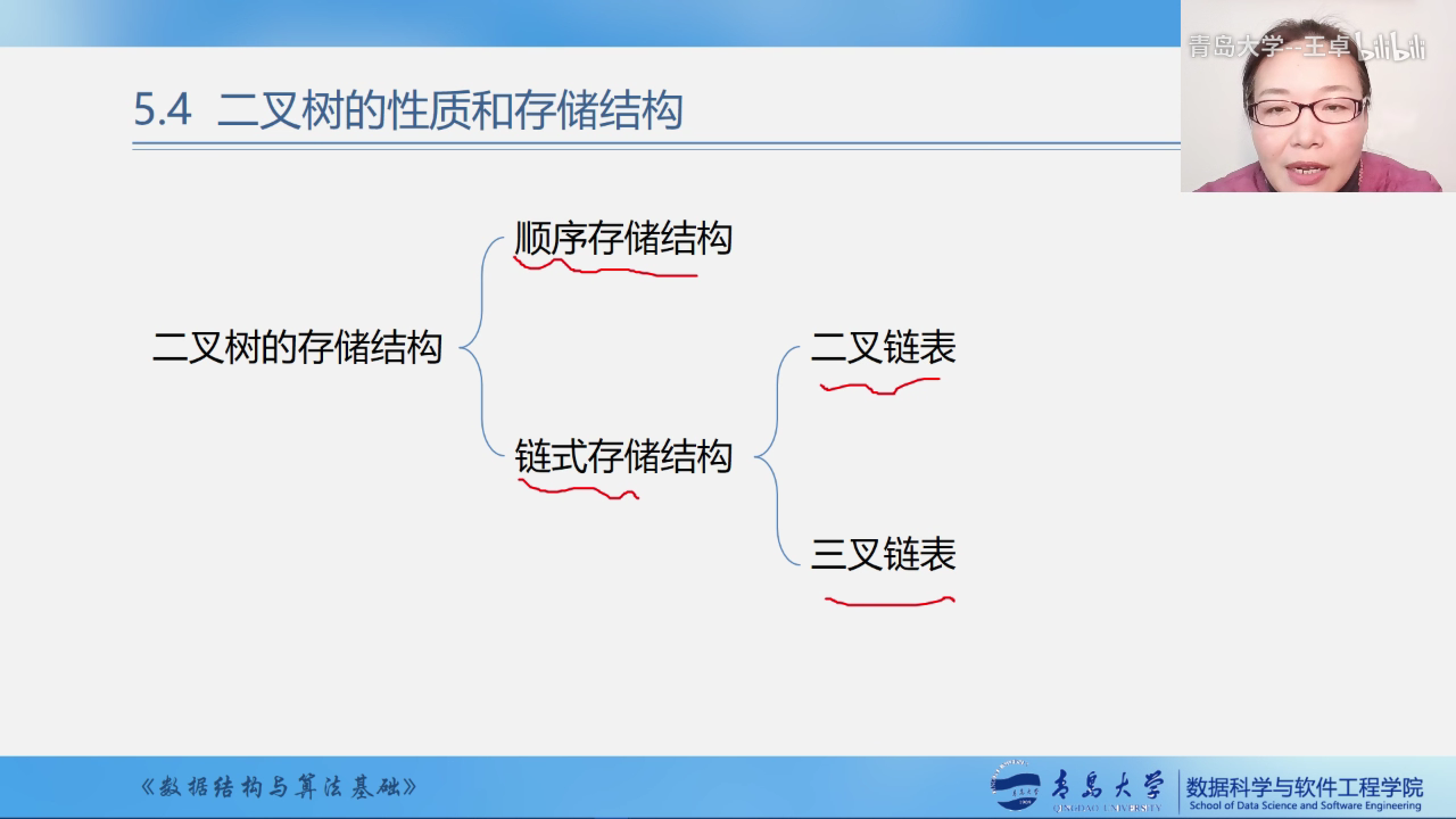
1.顺序存储结构(完全二叉树/满二叉树)
2.链式存储结构(一般二叉树).
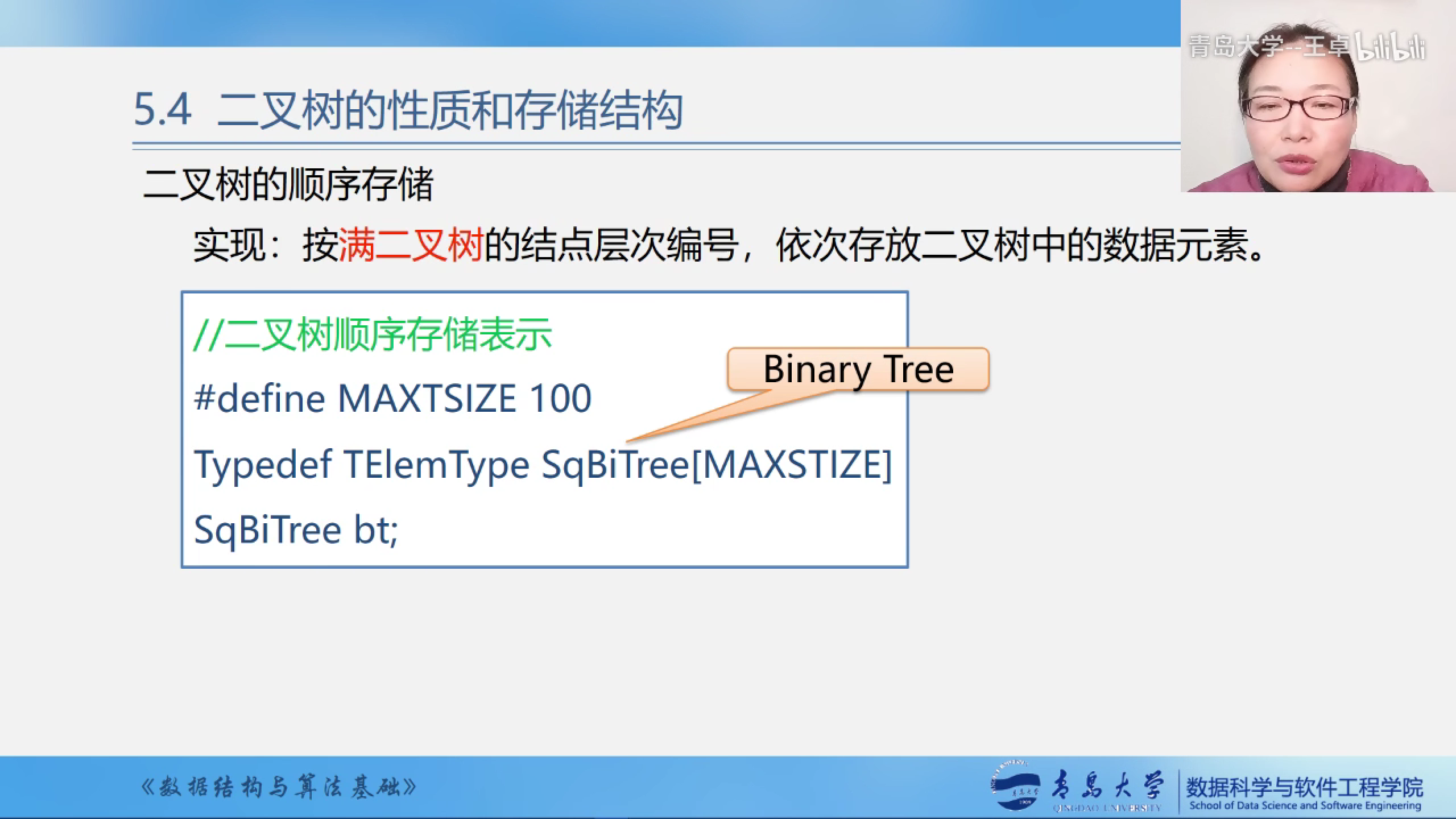
顺序存储结构
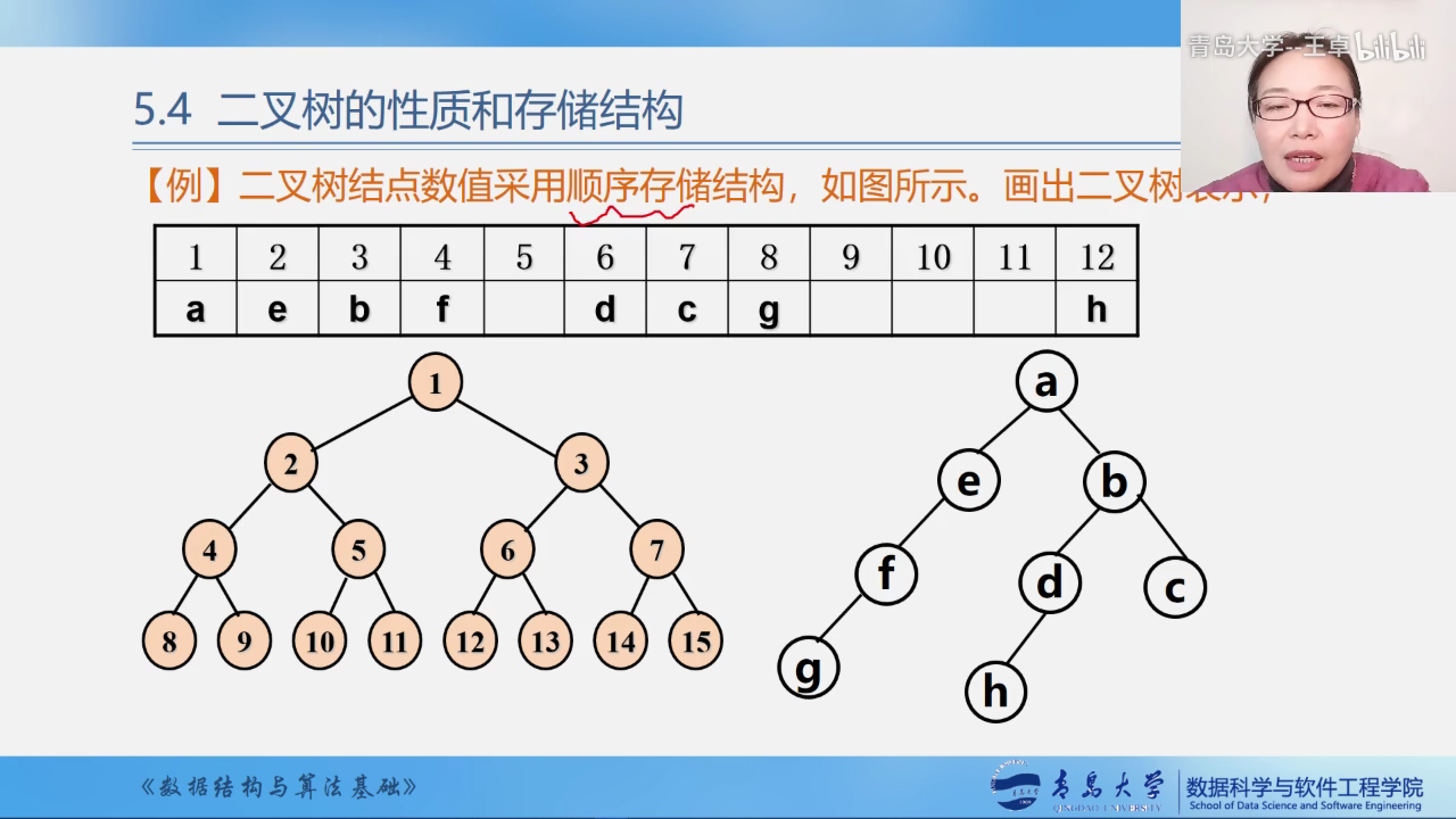
按照满二叉树的结点层次编号,然依次后储存在数组当中
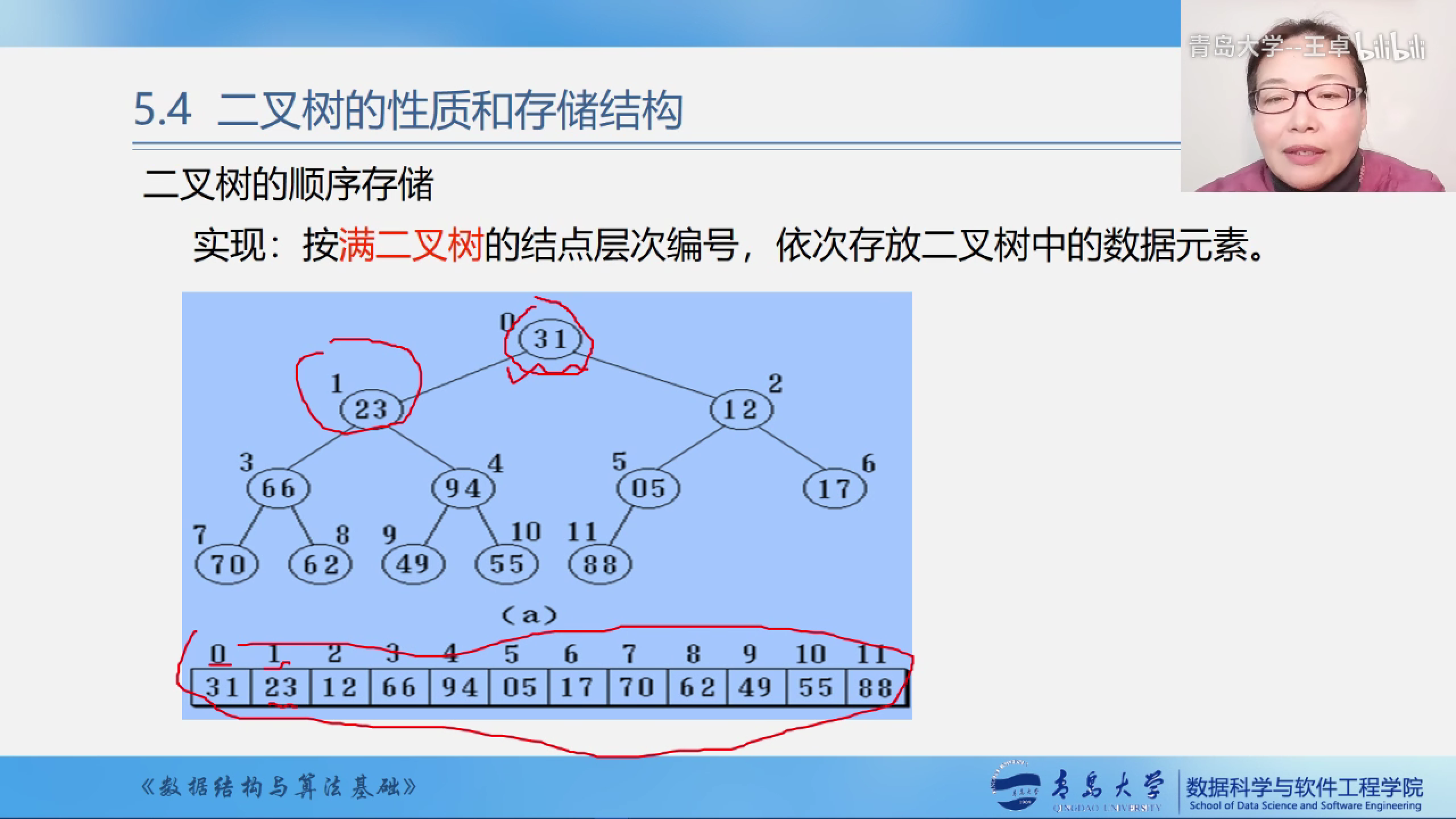
如果该二叉树中位置是空的再对应到数组中的时候就使用0来填充.
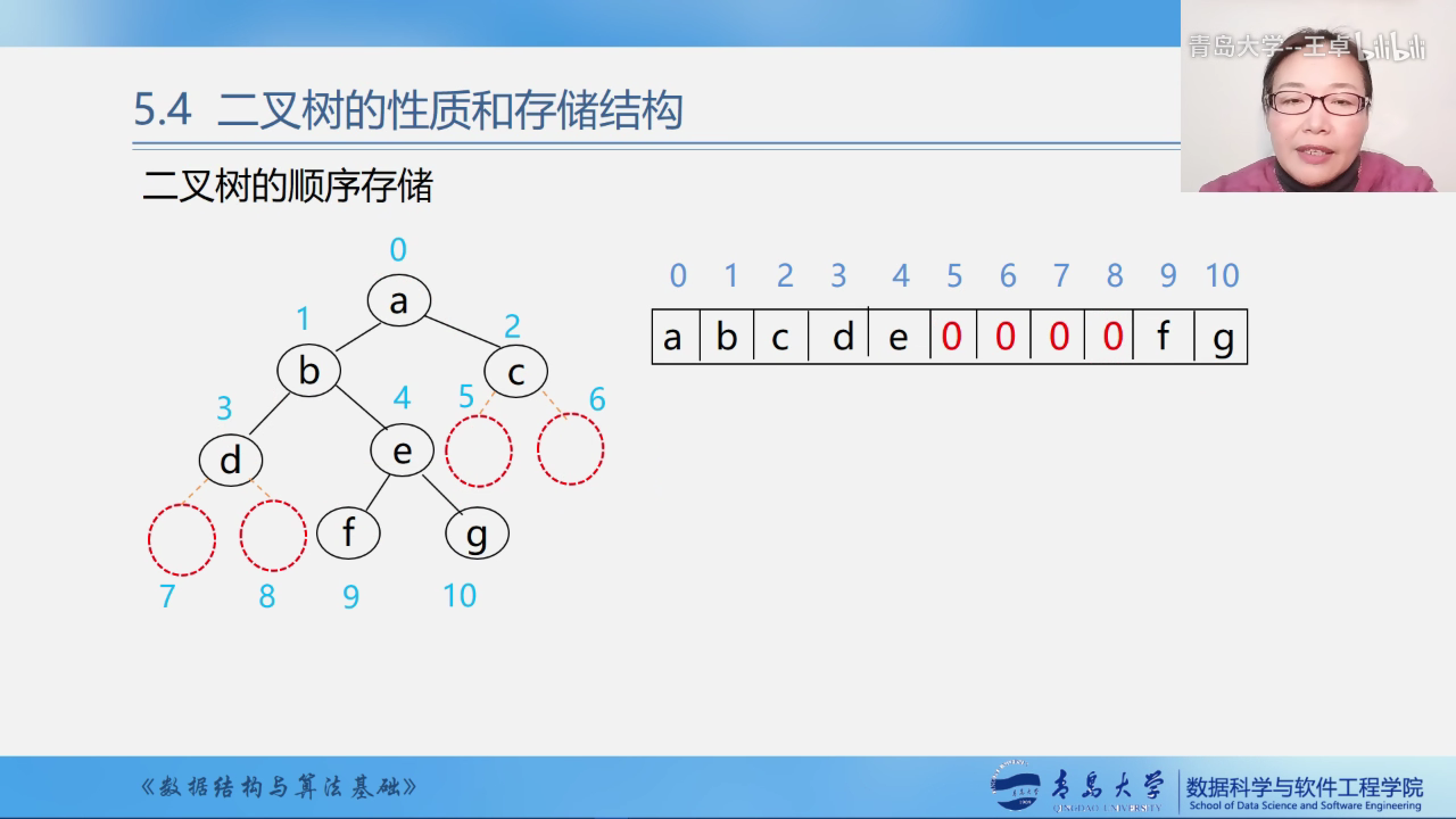
二叉树顺序存储结构的缺点
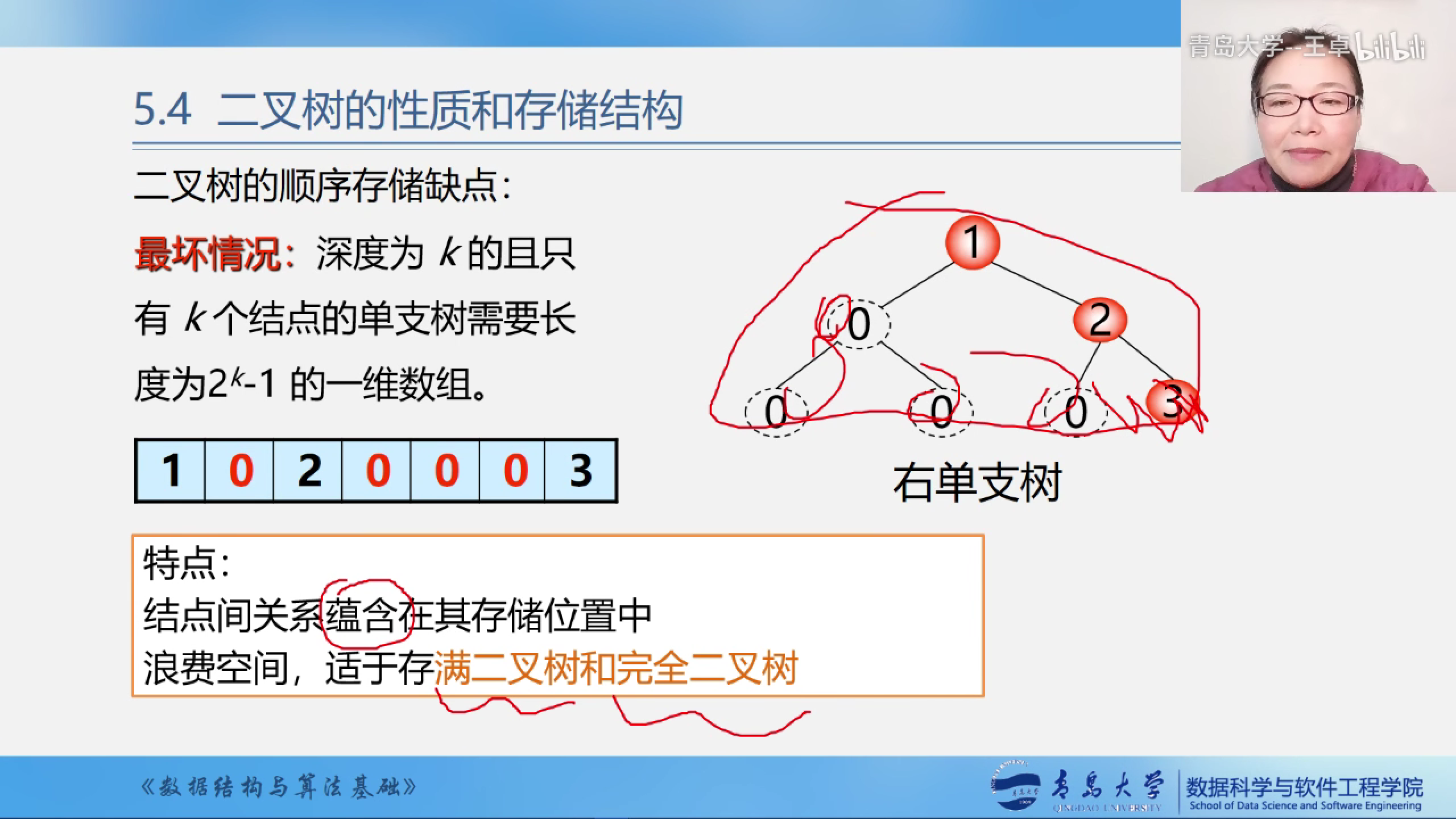
1.顺序存储结构不能动态的变化
2.如果二叉树退化为右单支树的时候非常浪费空间
所以顺序存储结构适用于满二叉树和完全二叉树
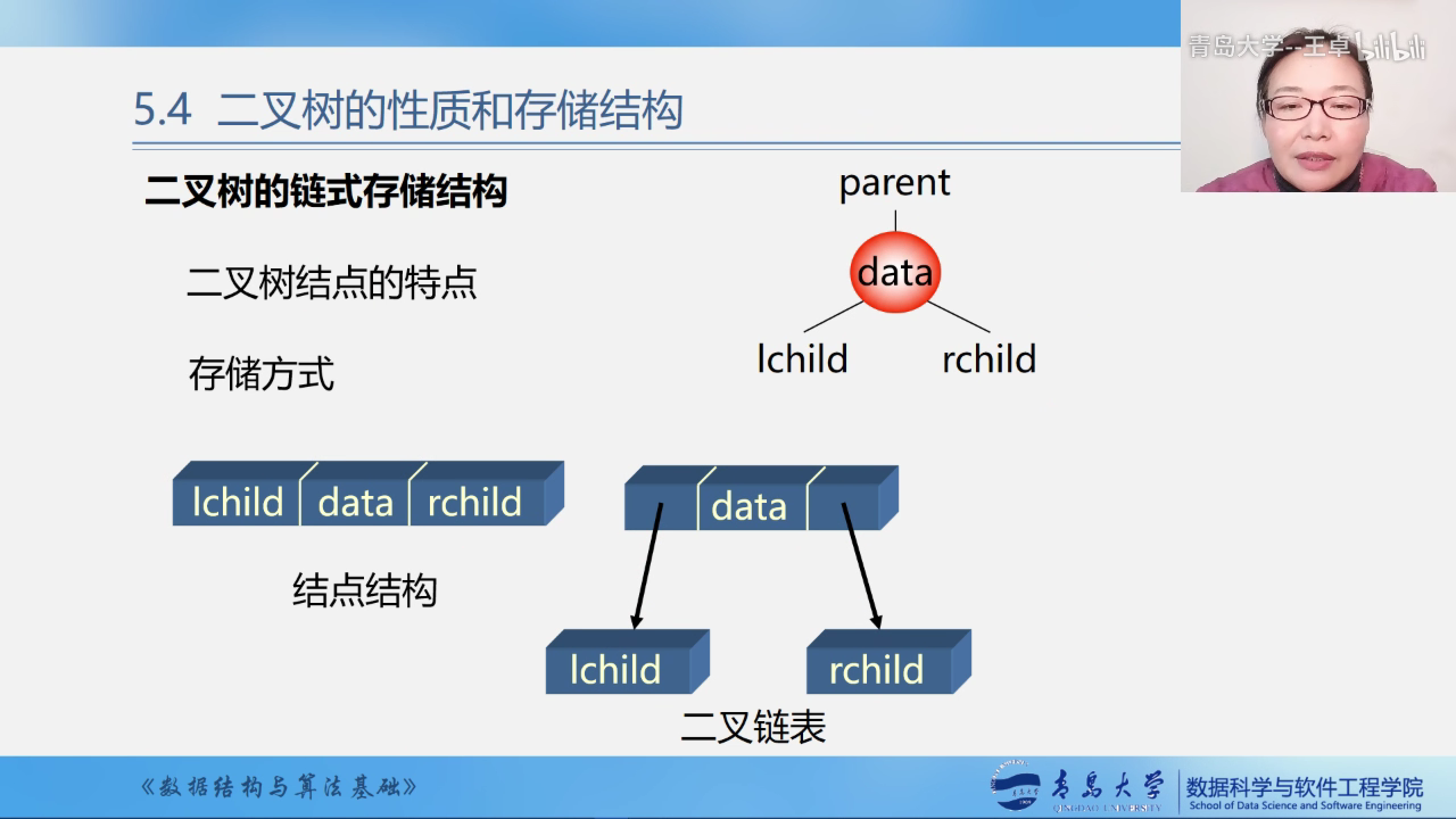
二叉树的链式存储结构
使用二叉链表储存二叉树,这样的存储结构可以动态扩展.
二叉链表示意图
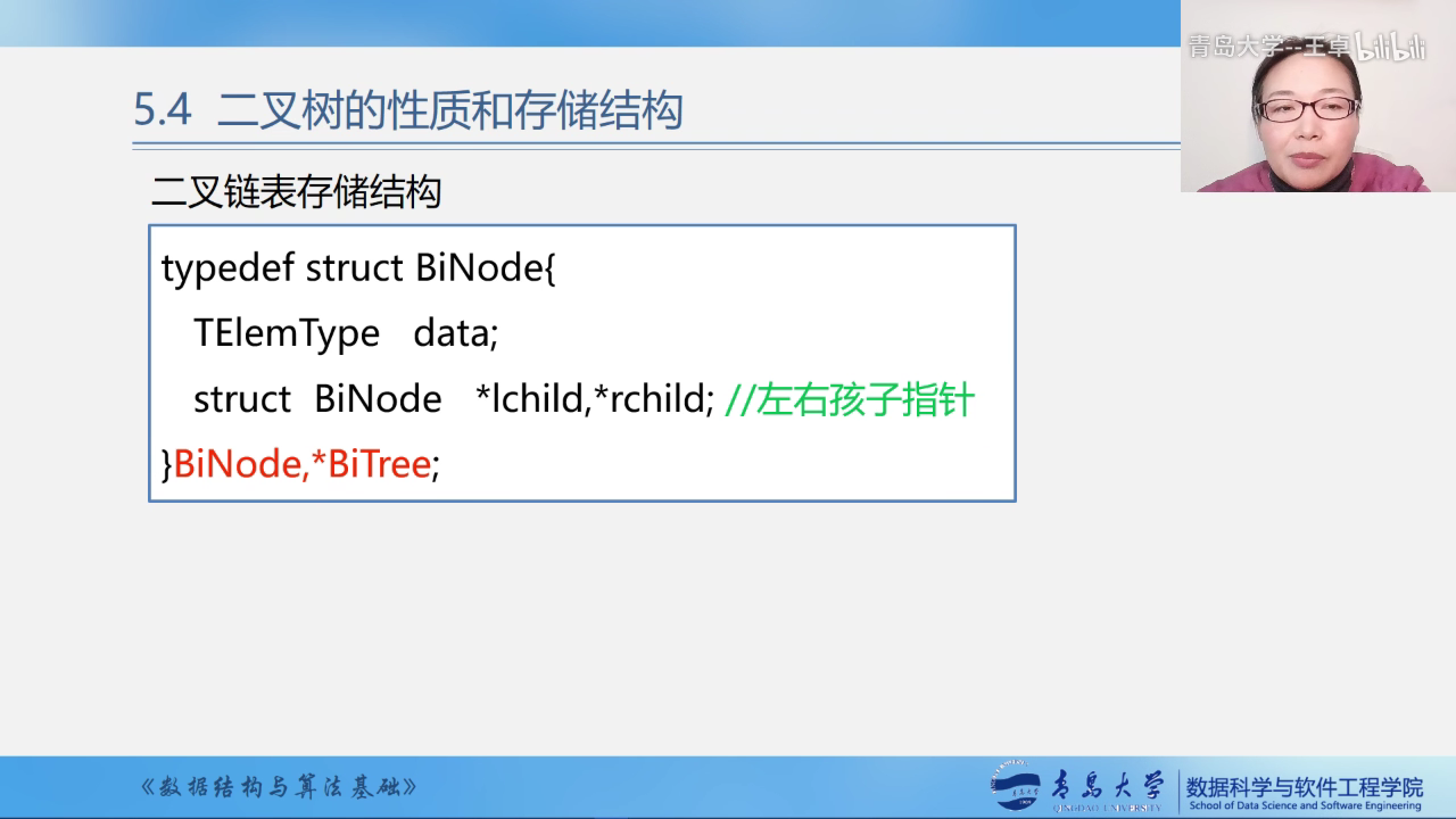
二叉链表的抽象数据结构
#include <iostream>
using namespace std;
typedef struct BiNode {
int data;//数据域
struct BiNode *lchild, *rchild; //左孩子指针和右孩子指针
} BiNode, *BiTree;
signed main () {
return 0;
}
二叉树链式存储示意图
两个指针域如果没有该方向没有孩子就设置为NULL,否则指向下一个结点,注意这里的二叉树的结点的定义是递归的定义的.
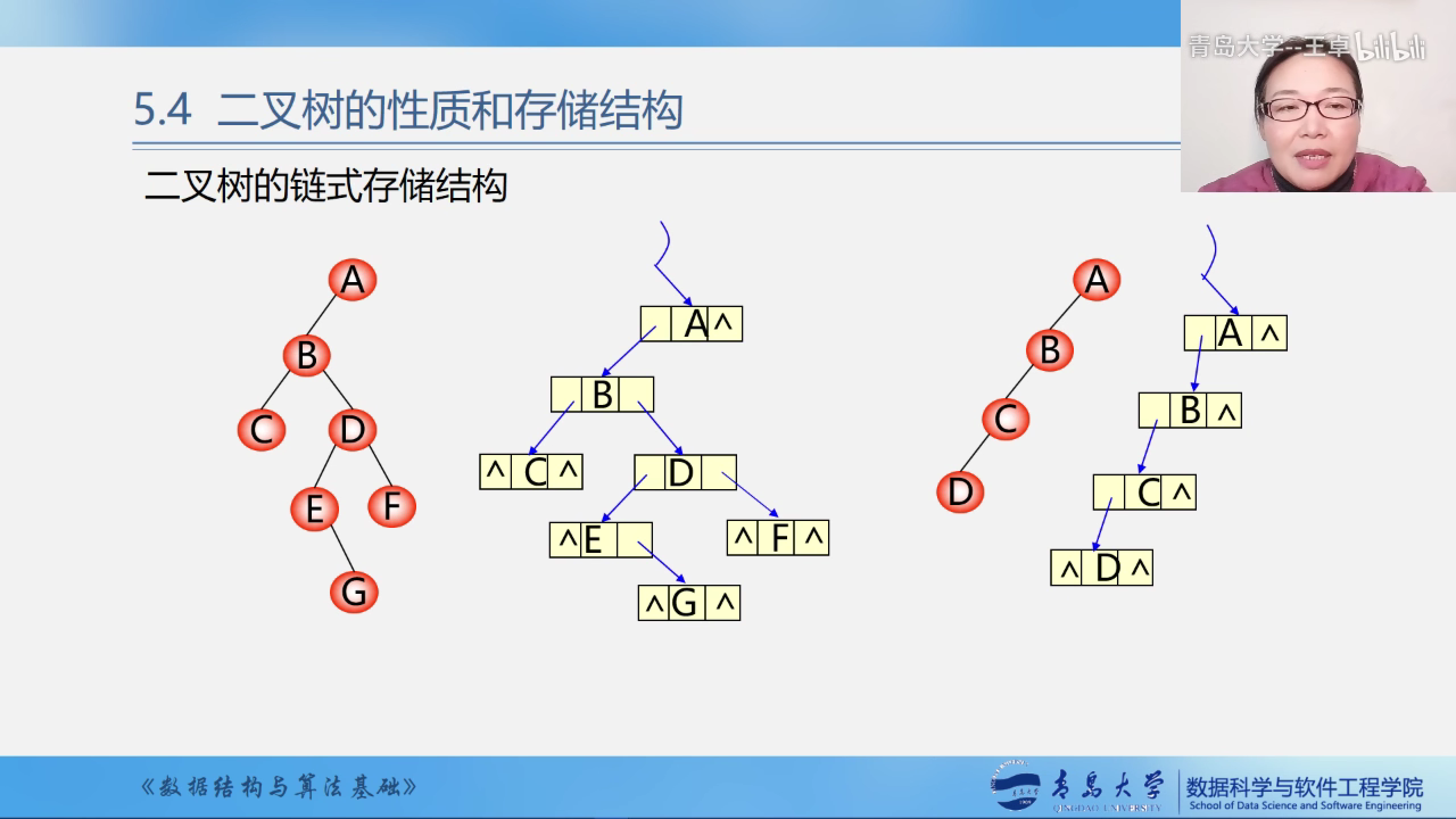
空指针域和结点的关系
可以从边上来看(蓝色的箭头),因为根结点是没有双亲的,所以只有n-1个结点有向上的蓝色箭头.因为n个结点有2n个指针域,所以由上面的规律可以看出有n-1个指针域不为空(都指向其孩子结点).所以2n-(n-1)为n+1所以有n+1个空指针域.
三叉链表
除了有指向左孩子和右孩子的指针还有一个指向双亲的指针,便于从当前结点找到双亲结点,以解决二叉链表无法找到其双亲结点的弊端.
但是总体来说还是二叉链表使用的较为频繁.
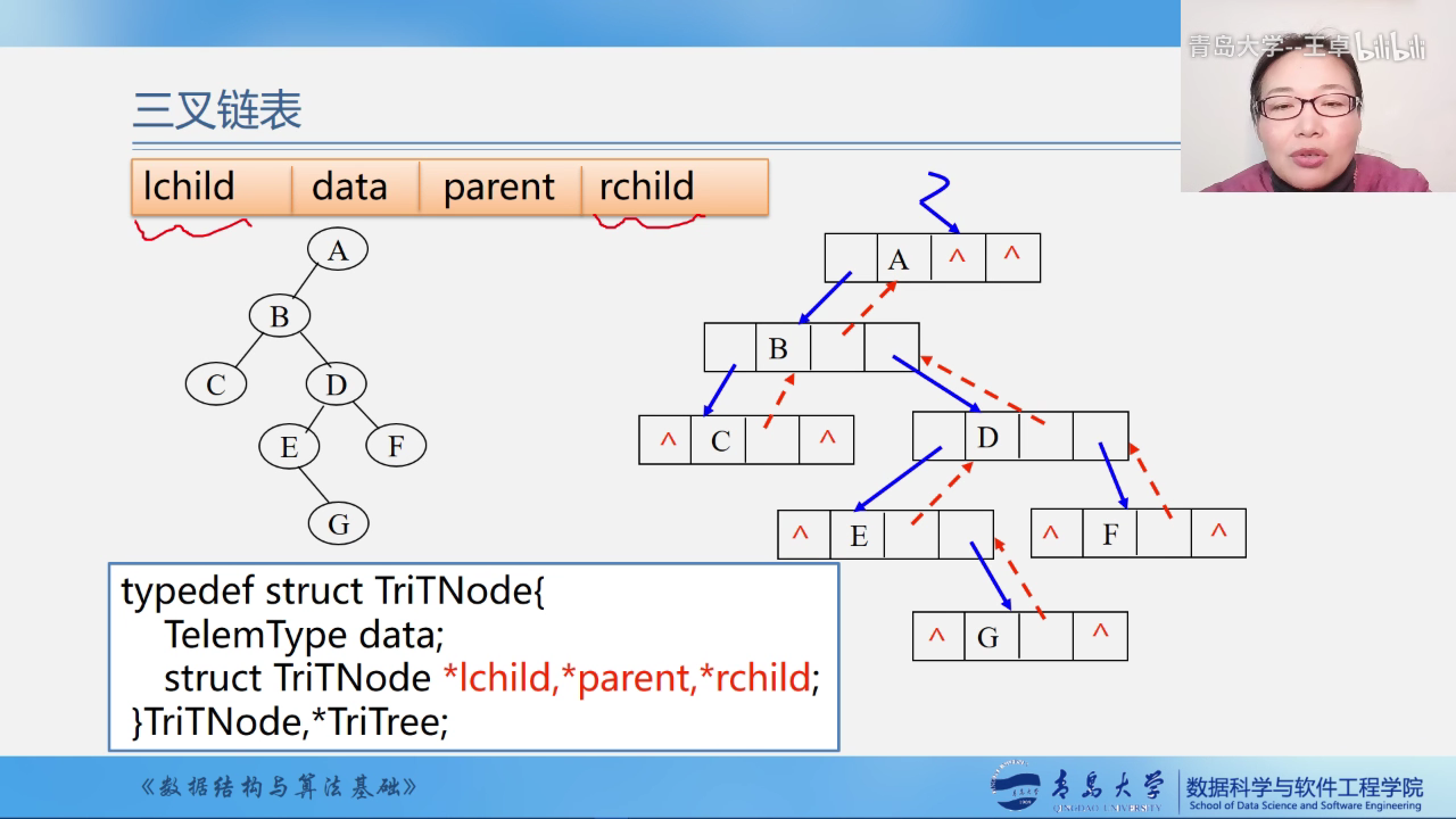
#include <iostream>
using namespace std;
typedef struct TriNode {
int data;
struct TriNode *lchild, *rchild, *parent; //左孩子指针,右孩子指针和双亲指针
} TriNode, *TirTree;
signed main () {
return 0;
}
二叉树的遍历算法
遍历二叉树
遍历的时候每个结点仅仅访问一次.
先序遍历:按照根,左子树,右子树的顺序遍历
中序遍历:按照先左子树,根和右子树的顺序遍历
后序遍历:按照先左子树,右子树和根的顺序遍历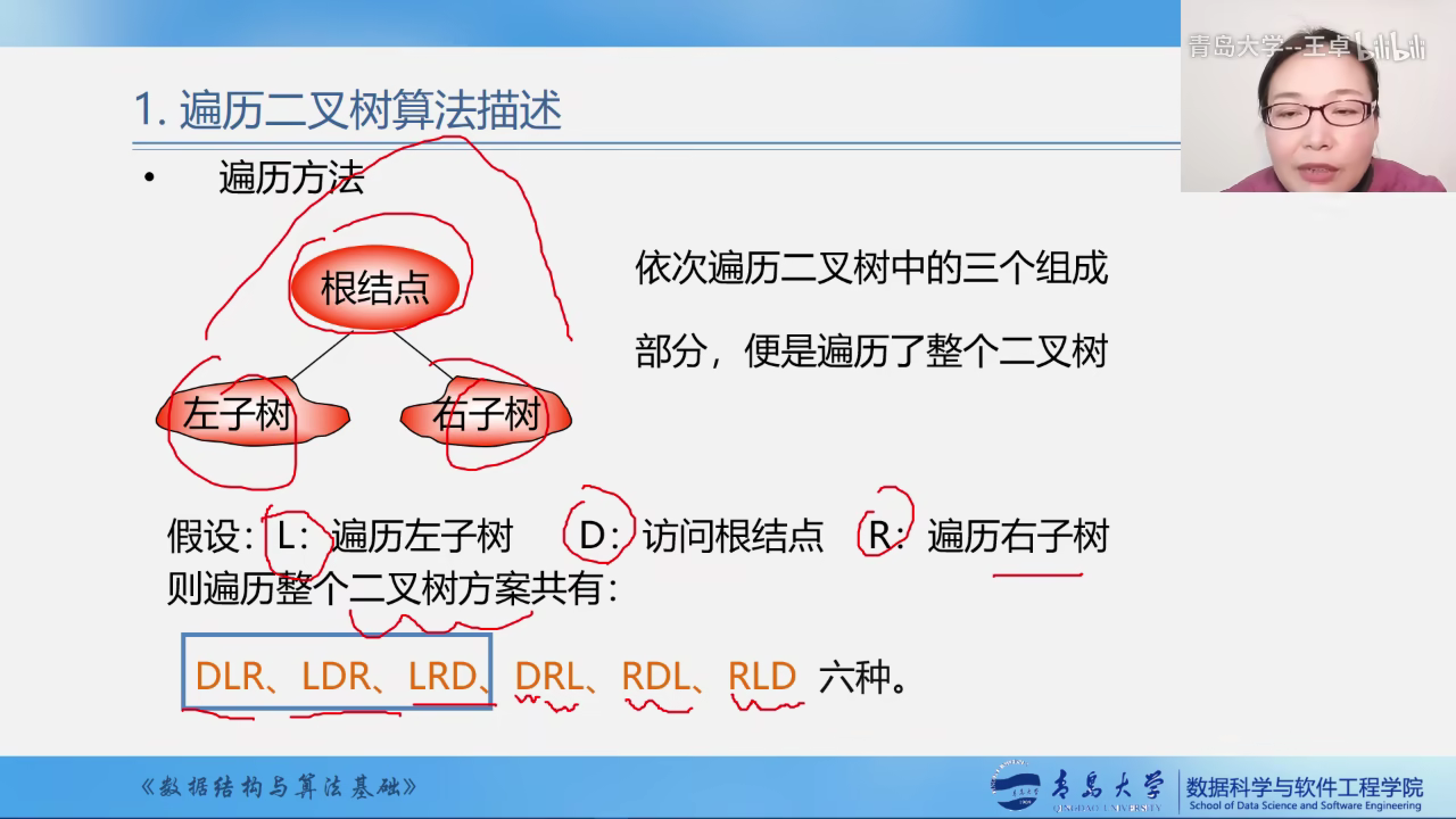
二叉树的遍历一般为DLR,LDR,LRD这几种方式
因为二叉树的定义是递归定义的,所以我们在进行遍历的时候进行递归的遍历就比较简单.
二叉树的先序遍历
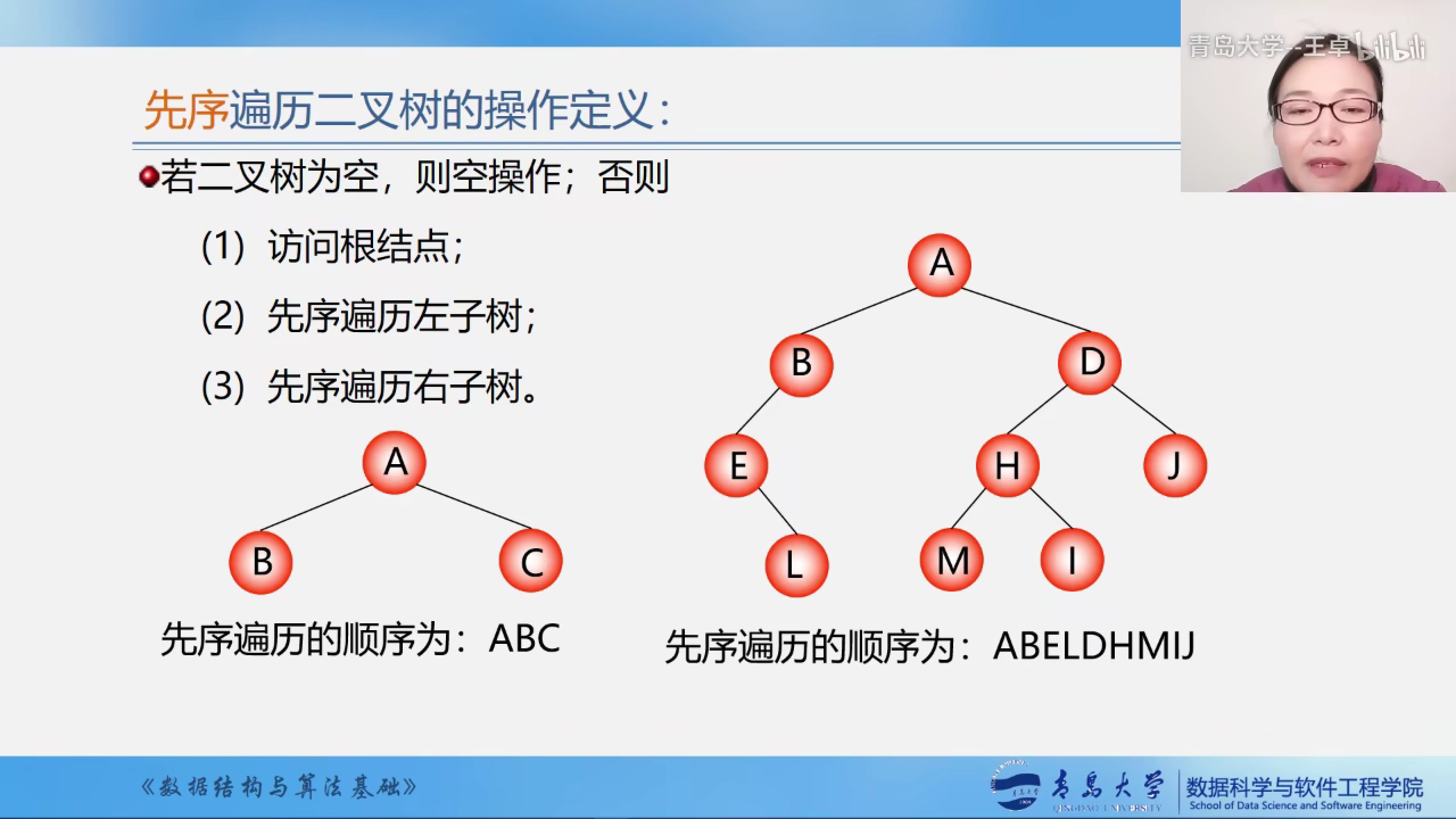
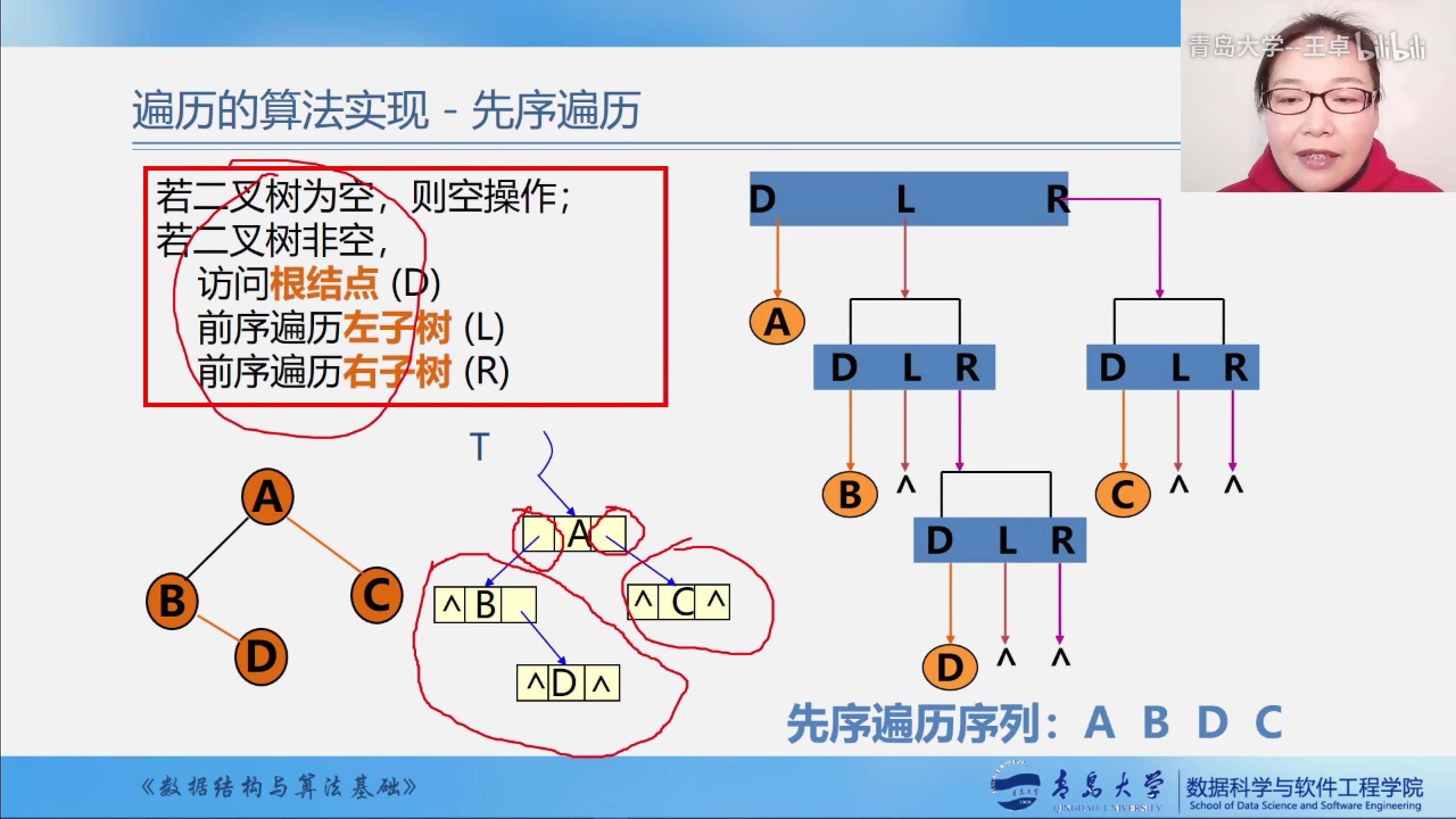
下面是二叉树的先序遍历算法.
算法执行过程分析
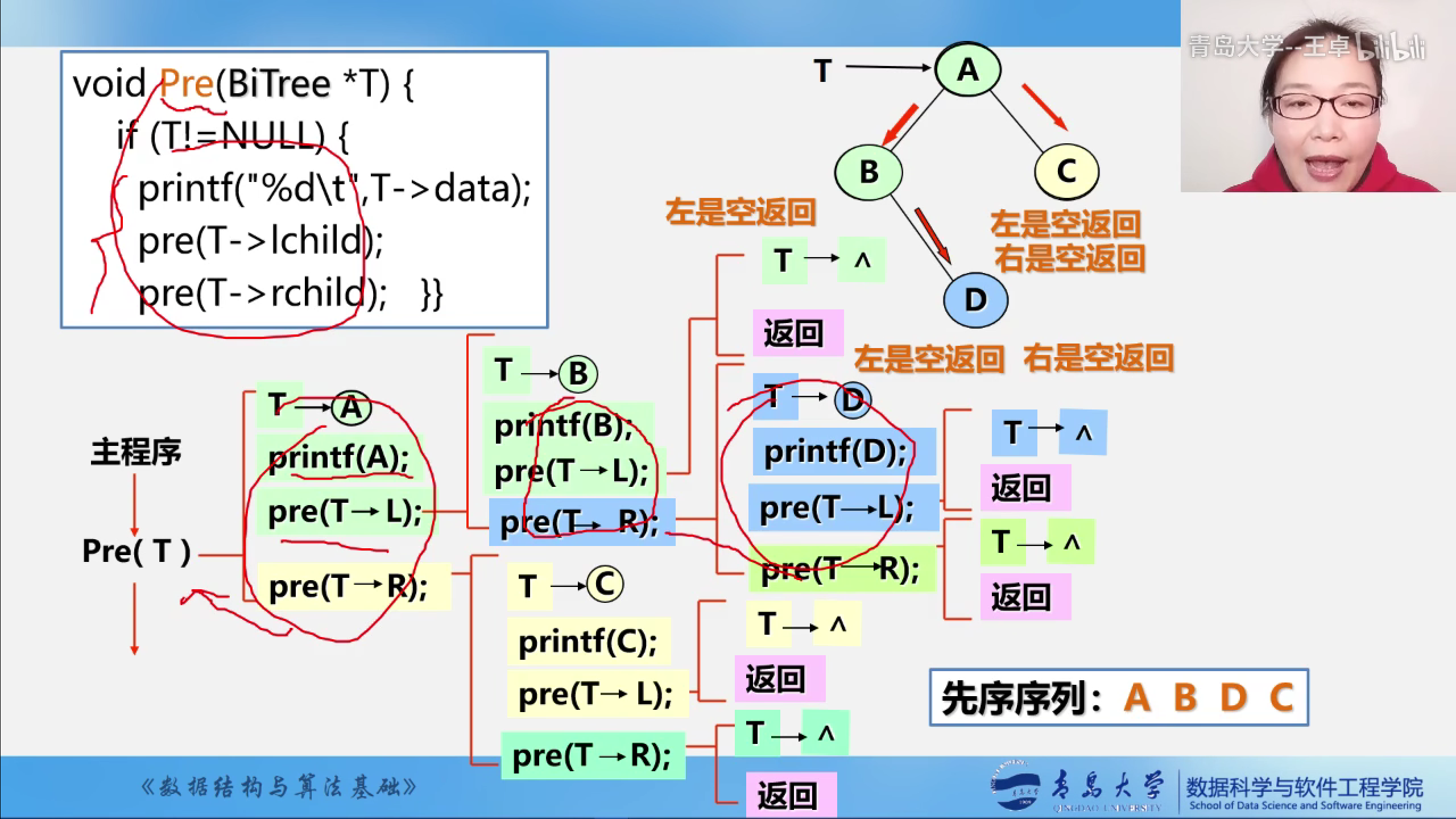
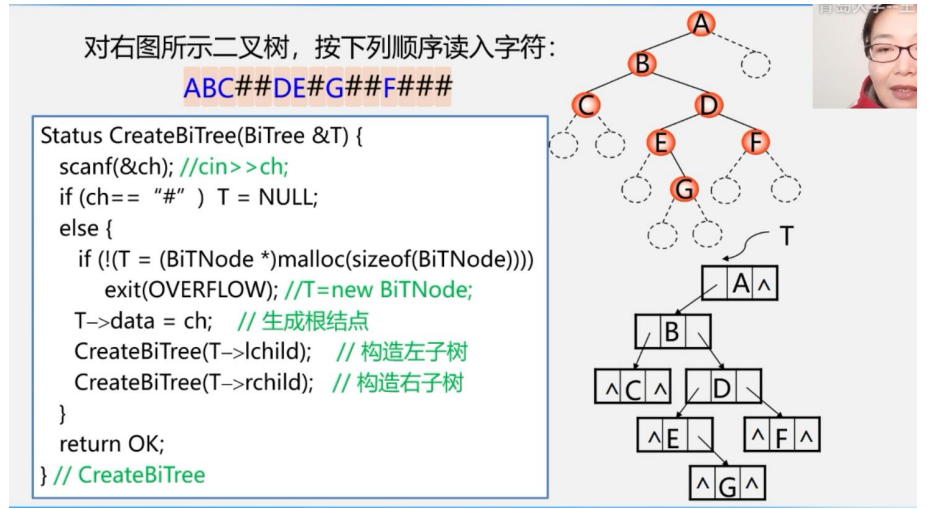
二叉的先序创建
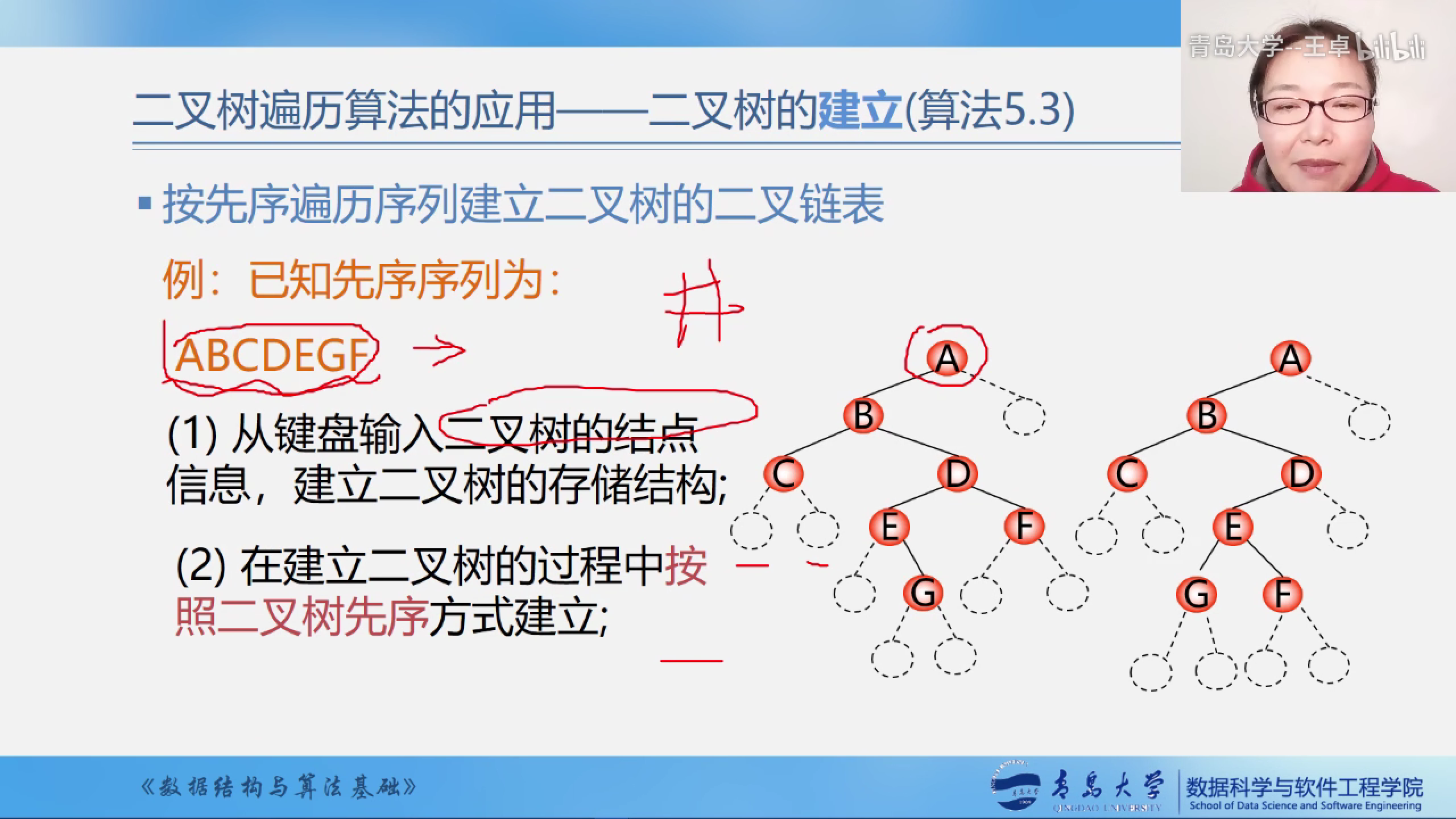
上面的例子说明只有二叉树的先序序列是不能够创建出唯一的二叉树序列的,只有将空结点补齐才能确定唯一的一颗二叉树
我们使用#号来表示该结点为空结点.
先进行先序创建然后进行先序遍历
#include <iostream>
using namespace std;
typedef struct BiNode {
char data;//数据域
struct BiNode *lchild;//左孩子指针
struct BiNode *rchild;//右孩子指针
} BiNode, *BiTree;//定义二叉树结点
/*
按照先序创建
*/
void CreateBiTree(BiTree &T) {
char ch;
cin >> ch;
if (ch == '#') {
T = NULL;
return;
} else {
T = new BiNode;//开辟结点
T->data = ch; //对数据域赋值
CreateBiTree(T->lchild);//建立左子树
CreateBiTree(T->rchild);//建立右子树
}
}
/*
先序遍历
*/
void DLR(BiTree T) {
if (T == NULL) {
return ;
} else {
char ch = T->data;
cout << ch;
DLR(T->lchild);
DLR(T->rchild);
}
}
/*
中序遍历
*/
void LDR(BiTree T) {
if (T == NULL) {
return ;
} else {
char ch = T->data;
LDR(T->lchild);//先访问左子树
cout << ch;//再访问根结点
LDR(T->rchild);//再访问右子树
}
}
/*
后序遍历
*/
void LRD(BiTree T) {
if (T == NULL) {
return ;
} else {
char ch = T->data;
LRD(T->lchild);//先访问左子树
LRD(T->rchild);//再访问右子树
cout << ch;//再访问根结点
}
}
int main () {
BiTree root = NULL;
CreateBiTree(root);
DLR(root);
cout << '\n';
// LDR(root);
// cout<<'\n';
// LRD(root);
return 0;
}
/*
abc##de#g##f###
*/
二叉树的中序遍历
1.先访问左子树
2.再访问根结点
3.最后访问右子树
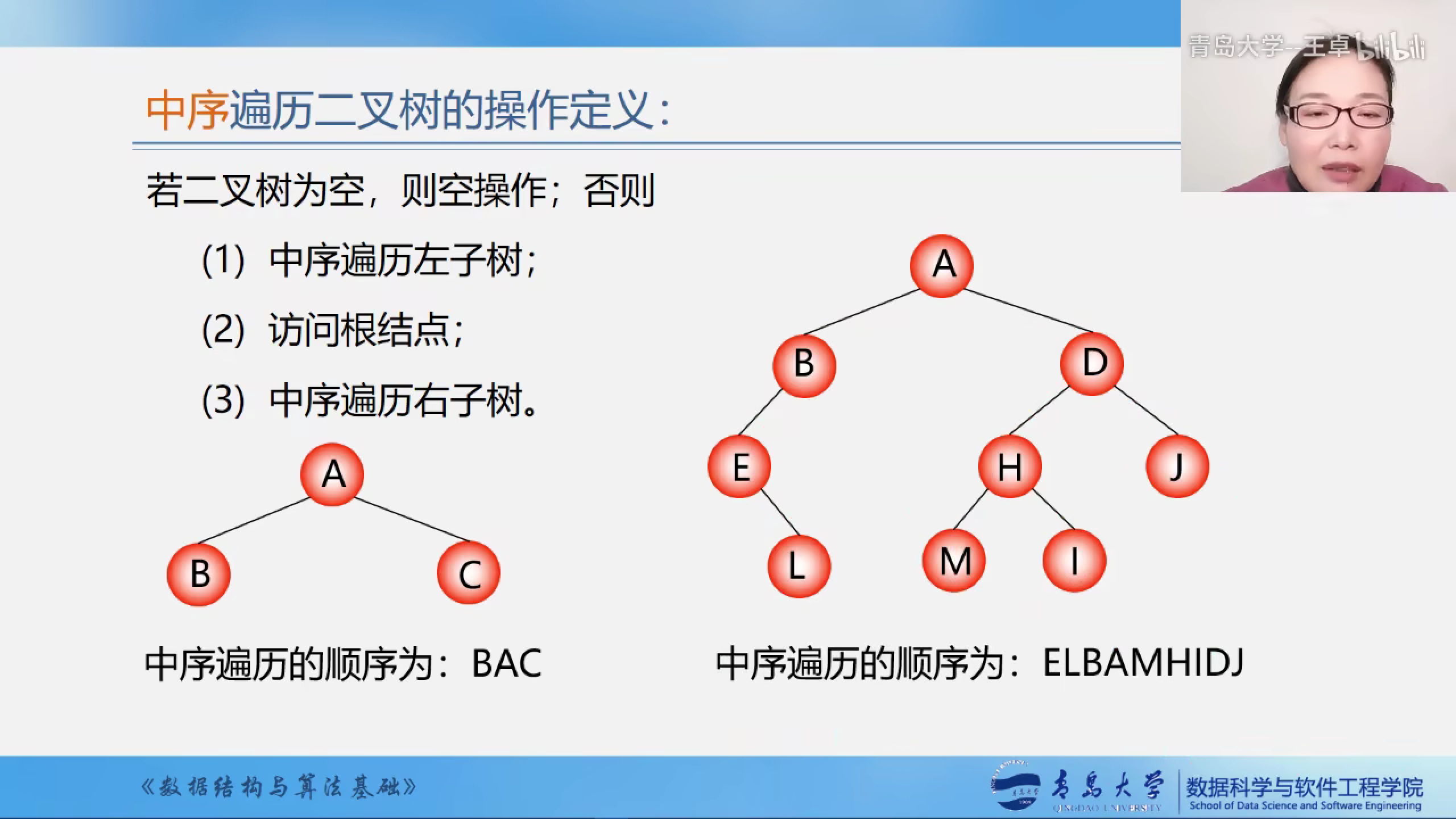
中序遍历示意图
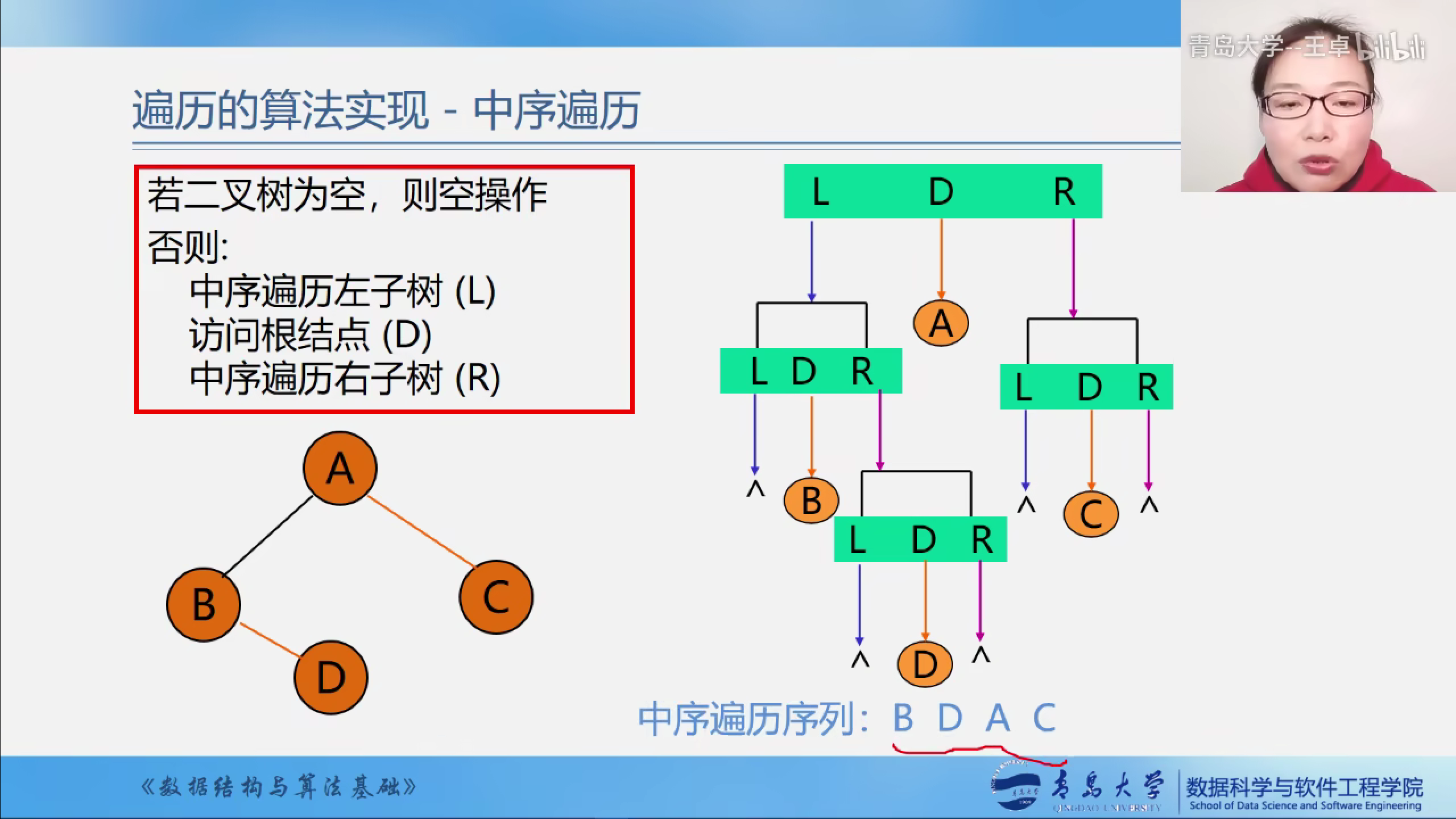
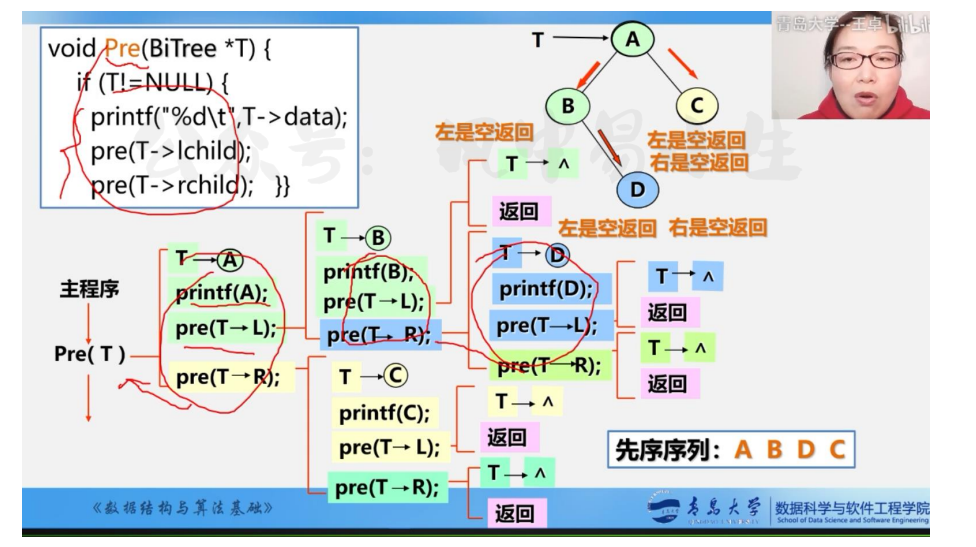
中序遍历算法实现,就只是将打印语句换到两个递归中间输出而已
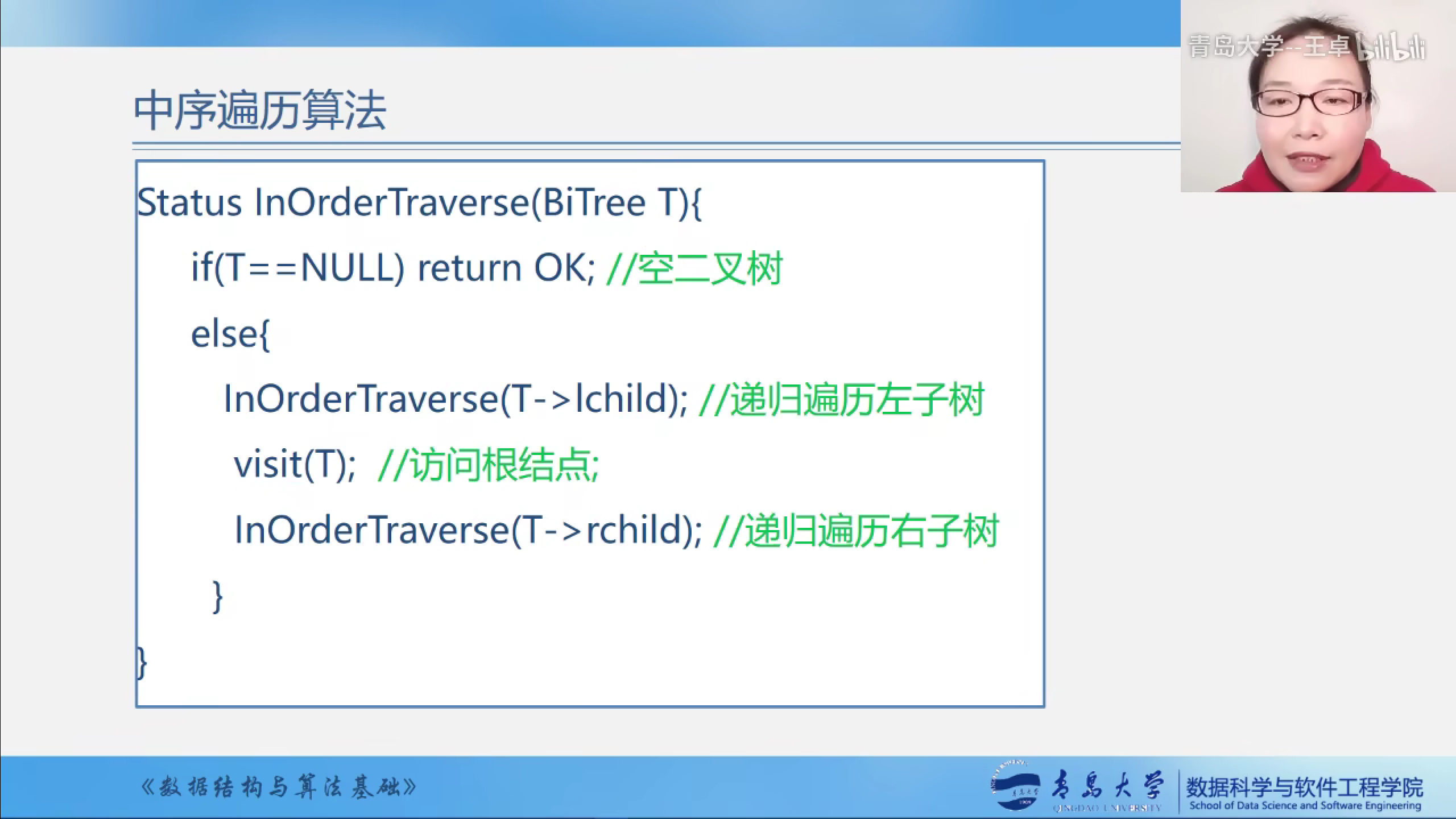
二叉树的后序遍历
-
先访问左子树
-
再访问右子树
-
最后访根结点
后序遍历的示意图
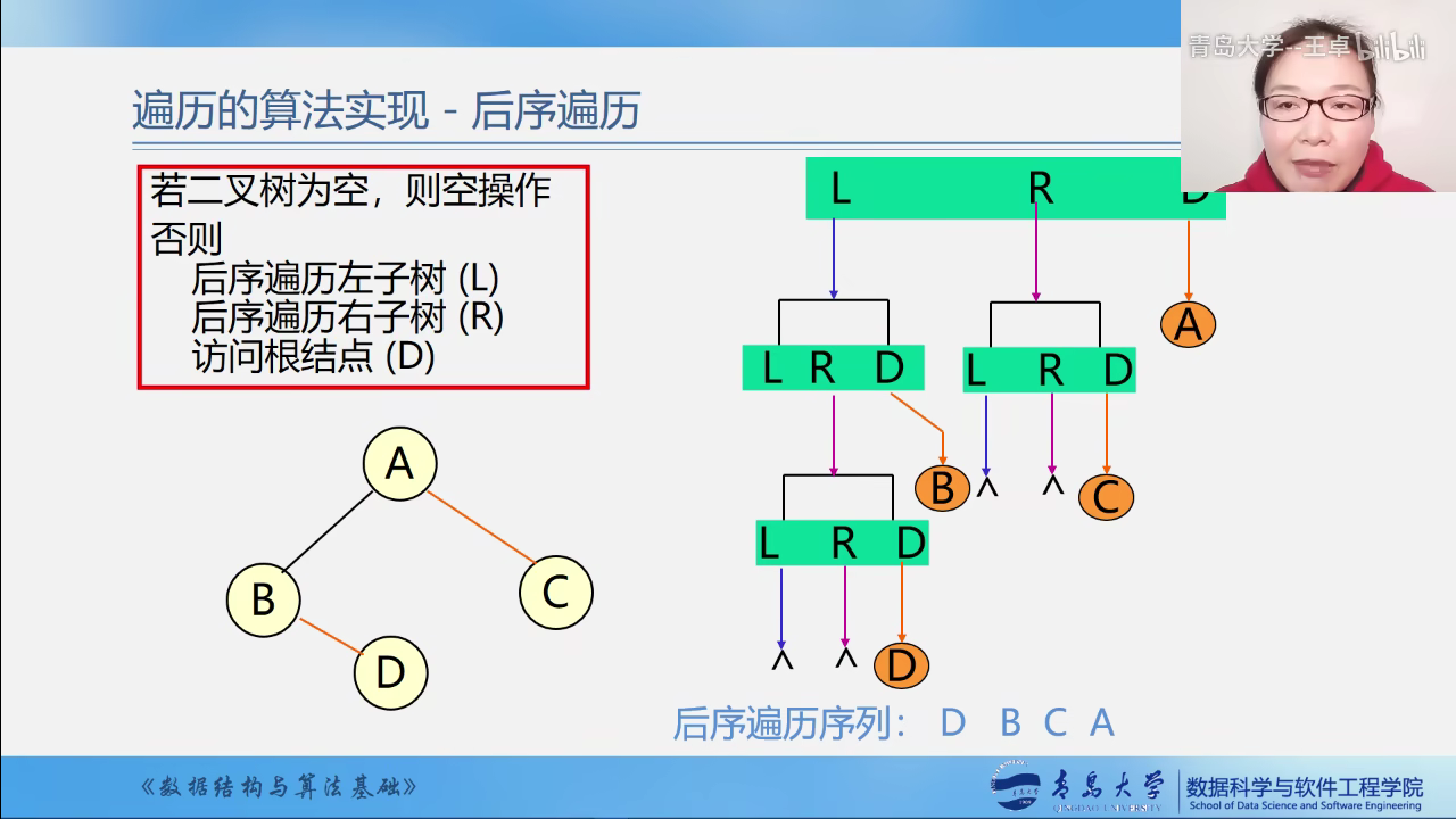
后序遍历的算法实现,将打印语句放在最后进行打印.
下面是一个例题
先序:ABDGCEHF
中序:DGBAEHCF
后序:GDBHEFCA
完整代码演示
#include <iostream>
using namespace std;
typedef struct BiNode {
struct BiNode *lchild, *rchild;//左孩子右孩子
char data;//数据域
} BiNode, *BiTree;
/*
二叉树的先序创建
*/
void CreateBitree(BiTree &T) {
char ch;
cin >> ch;
if (ch == ',') {
T = NULL; //,表示该结点为空
} else {
T = new BiNode; //创建一个新结点
T->data = ch; //给数据域赋值
CreateBitree(T->lchild);//建立左子树
CreateBitree(T->rchild);//建立右子树
}
}
/*
二叉树的先序遍历
*/
void DLR(BiTree T) {
if (T == NULL) {
return;
} else {
cout << T->data; //先访问根
DLR(T->lchild);//访问左子树
DLR(T->rchild);//访问右子树
}
}
/*
二叉树的中序遍历
*/
void LDR(BiTree T) {
if (T == NULL) {
return;
} else {
LDR(T->lchild);//访问左子树
cout << T->data; //访问根
LDR(T->rchild);//访问右子树
}
}
/*
二叉树的后序遍历
*/
void LRD(BiTree T) {
if (T == NULL) {
return;
} else {
LRD(T->lchild);//访问左子树
LRD(T->rchild);//访问右子树
cout << T->data; //访问根
}
}
signed main () {
BiTree root = NULL; //创建根结点
cout << "请输入需要建立的二叉树的数值\n";
CreateBitree(root);//创建二叉树
cout << "下面是二叉树先序遍历结果\n";
DLR(root);
cout << "\n下面是二叉树中序遍历结果\n";
LDR(root);
cout << "\n下面是二叉树后序遍历结果\n";
LRD(root);
return 0;
}
/*
abc,,de,g,,f,,,
中序:
cbegdfa
后序:
cgefdba
*/
二叉树的中序非递归算法
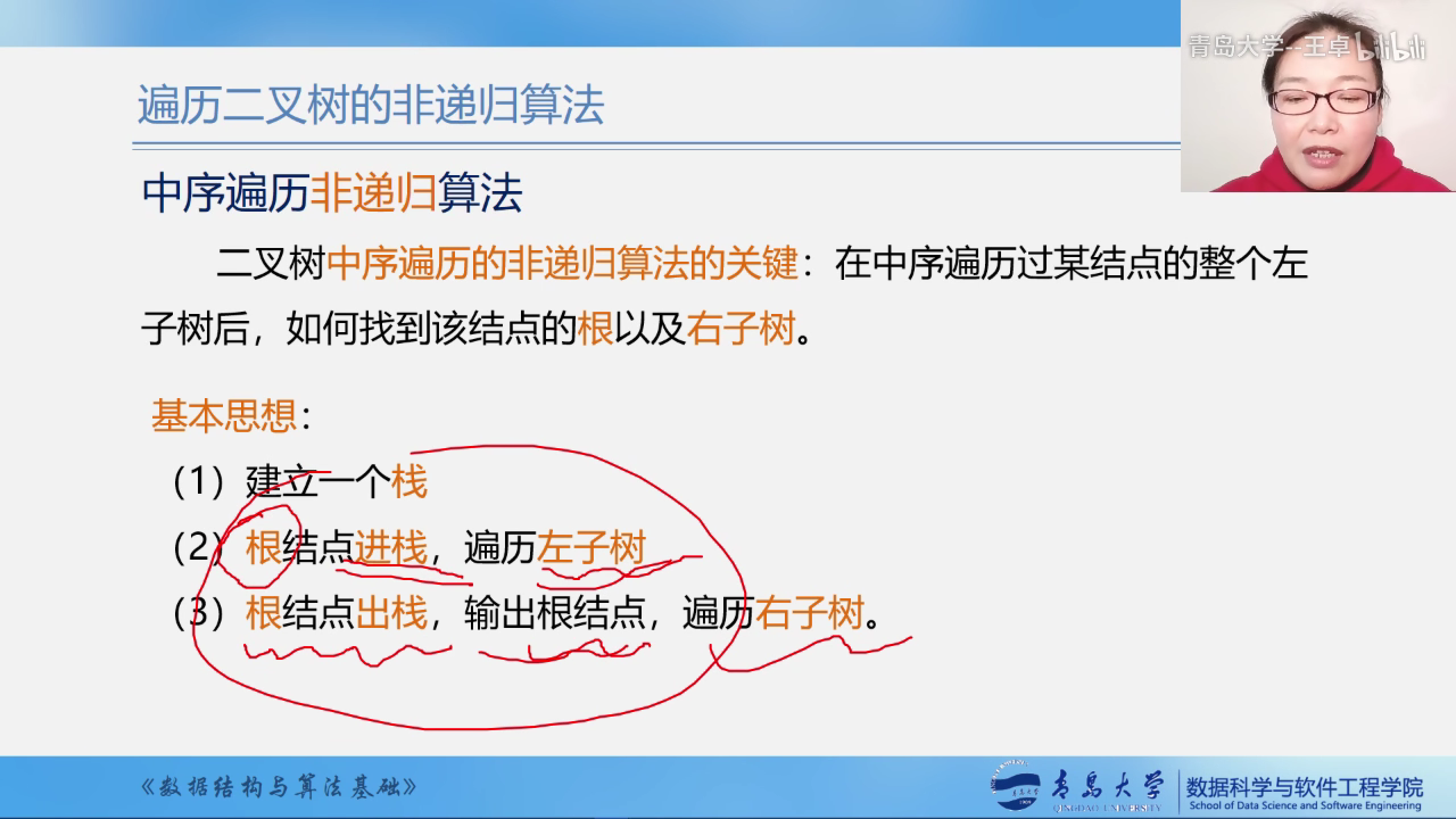
前面我们学过,任何递归的过程我们都可以改造成非递归的方式,所以二叉树的递归遍历也可以改造成非递归的遍历方式.
算法示意图
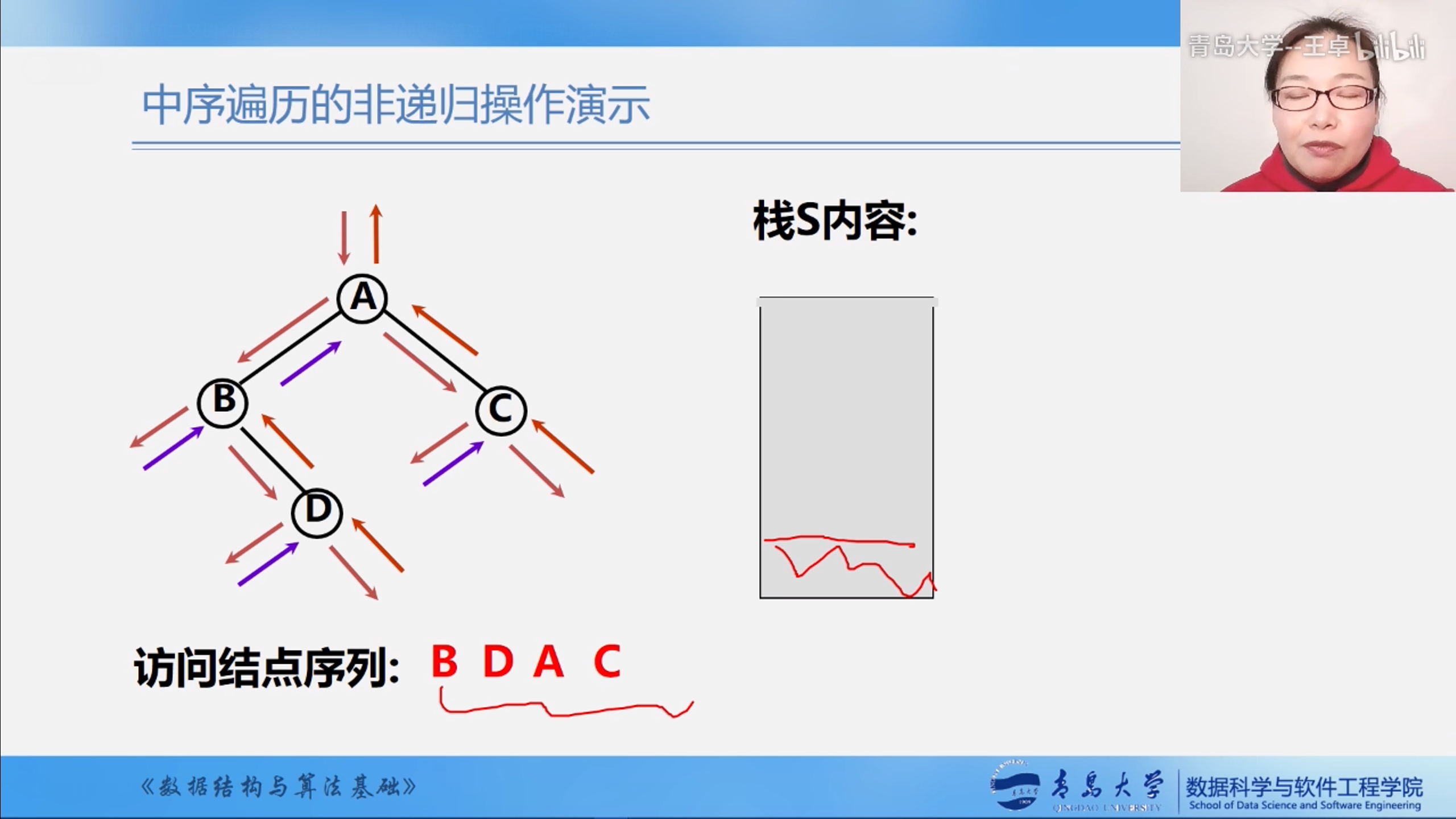
自己用栈来模拟这个过程
1.遇到根结点根结点入栈,遍历左子树
2.如果当前的P指针为NULL,弹栈,遍历右子树
当栈和P都为空的时候结束遍历
伪代码
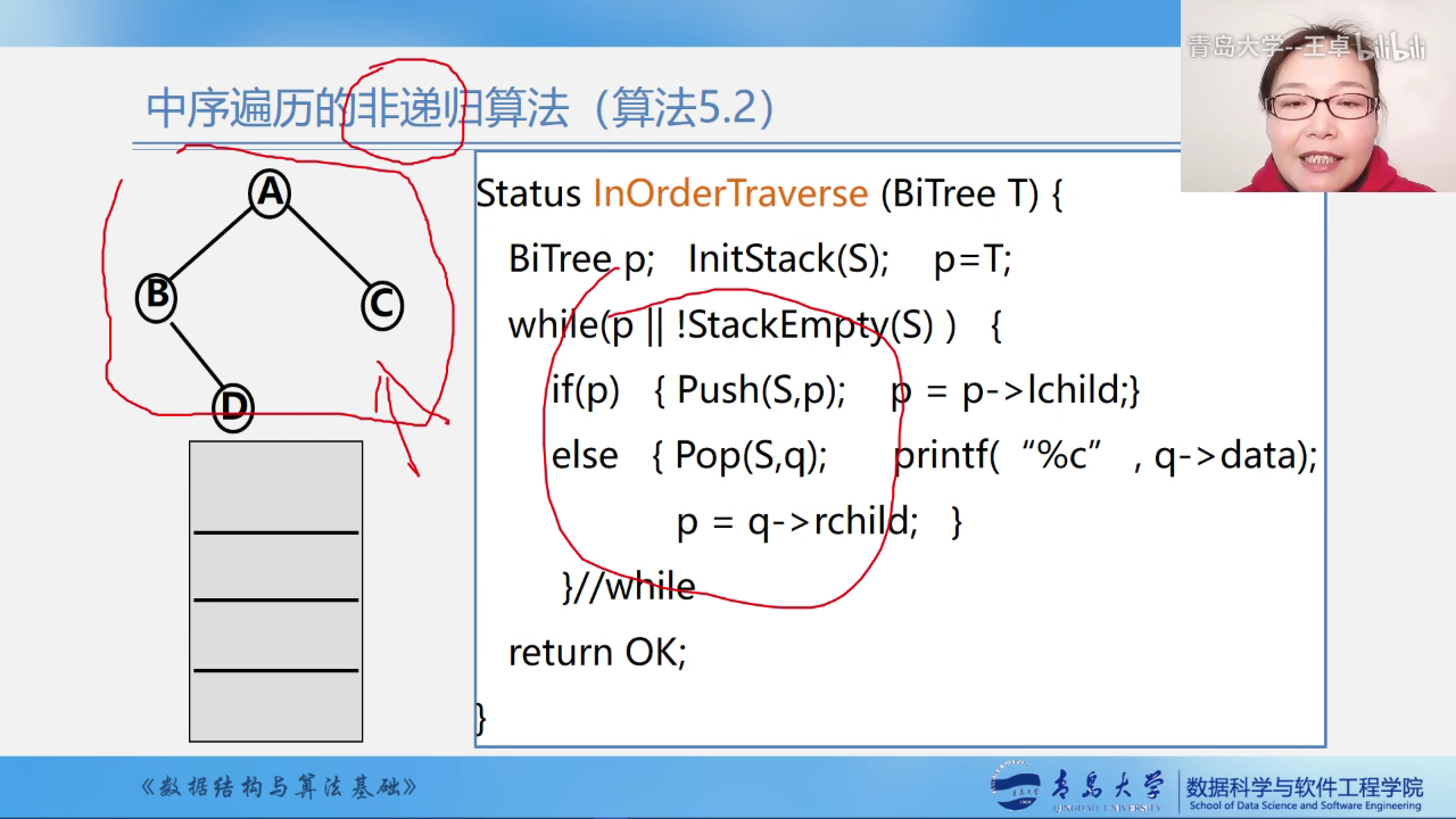
真正代码实现
我们使用C++里面的STL来实现这个过程
#include <iostream>
using namespace std;
typedef struct BiNode {
char data;//数据域
struct BiNode *lchild, *rchild; //左孩子右孩子
} BiNode, *BiTree;
/*
前序建立二叉树
*/
void CreateBitree(BiTree &T) {
char ch;
cin >> ch;
if (ch != '#') {
T = new BiNode;
T->data = ch; //写入根结点
CreateBitree(T->lchild);//建立左子树
CreateBitree(T->rchild);//建立右子树
} else {
T = NULL;
return;
}
}
/*
递归中序遍历
*/
void LDR(BiTree T) {
if (T != NULL) {
LDR(T->lchild);//先访问左子树
cout << T->data; //打印根结点
LDR(T->rchild);//访问右子树
} else {
return;
}
}
/*
非递归中序遍历
*/
void InOrderTraverse(BiTree T) {
stack <BiTree> s;//使用STL的栈
BiTree p = T; //让p指向根结点
while (p != NULL || s.empty() == false) { //当p不为空和栈不为空的时候进行循环
if (p != NULL) {
s.push(p);//如果根结点不为空,把根节点放入栈当中
p = p->lchild; //让p指向自己的右孩子
} else { //如果p为空
//先对栈顶元素出栈
cout << s.top()->data; //打印栈顶元素
p = s.top()->rchild; //让p指向栈顶元素指针的右孩子
s.pop();//弹出栈顶元素
}
}
}
signed main () {
BiTree root = NULL;
CreateBitree(root);
cout << "正在进行递归中序遍历\n";
LDR(root);
cout << '\n';
cout << "正在进行非递归中序遍历\n";
InOrderTraverse(root);
cout << '\n';
return 0;
}
/*
abc##de#g##f###
*/
二叉树的层次遍历
先从上到下在从左到右的遍历一颗二叉树
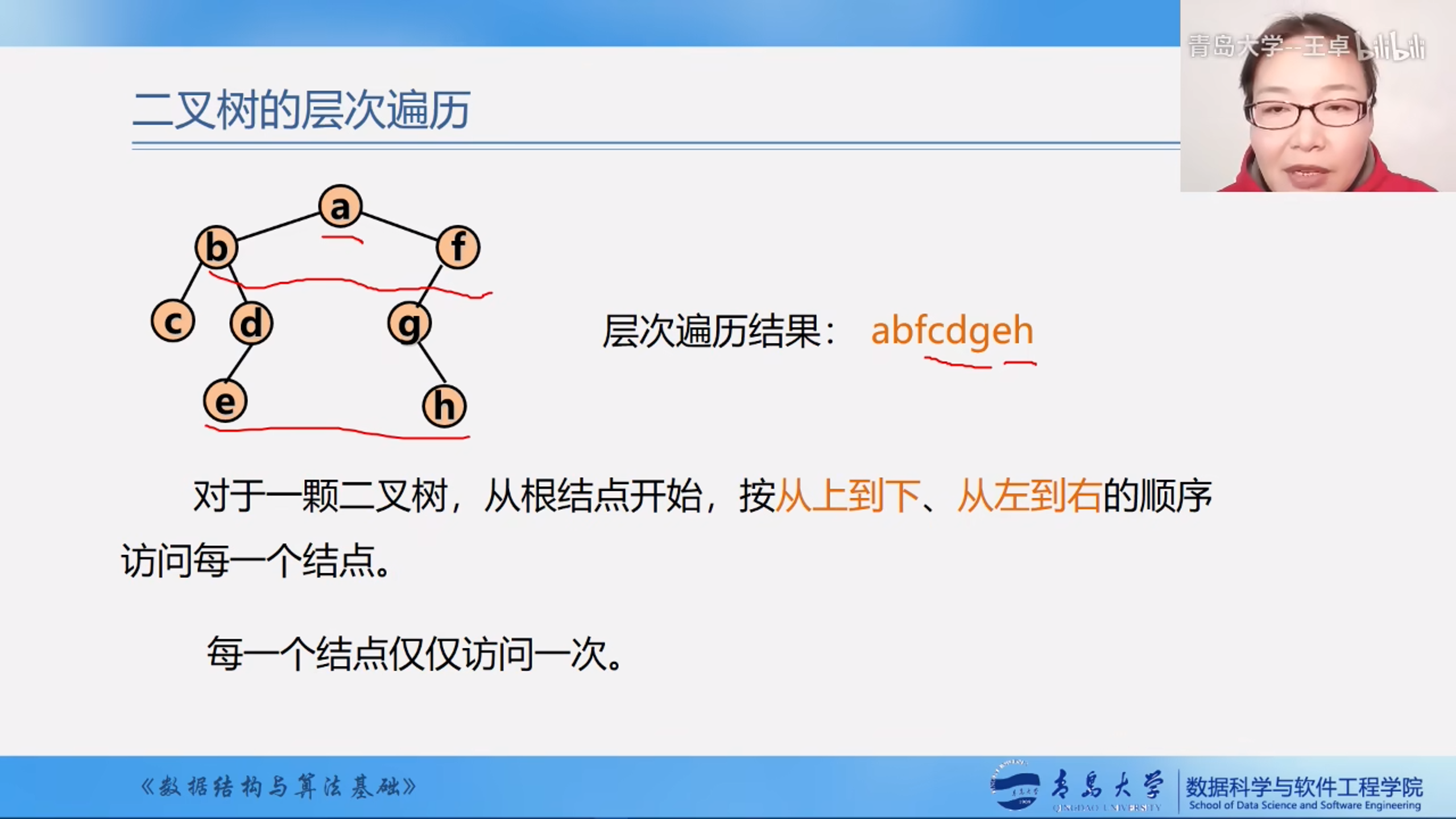
其实就是将一颗二叉树进行BFS遍历,然后打印遍历的顺序序列.
找一个队列,将根结点入队,然后每次取出队头然后向后面扩展,知道队列为空为止,队列我们可以使用STL中的队列.
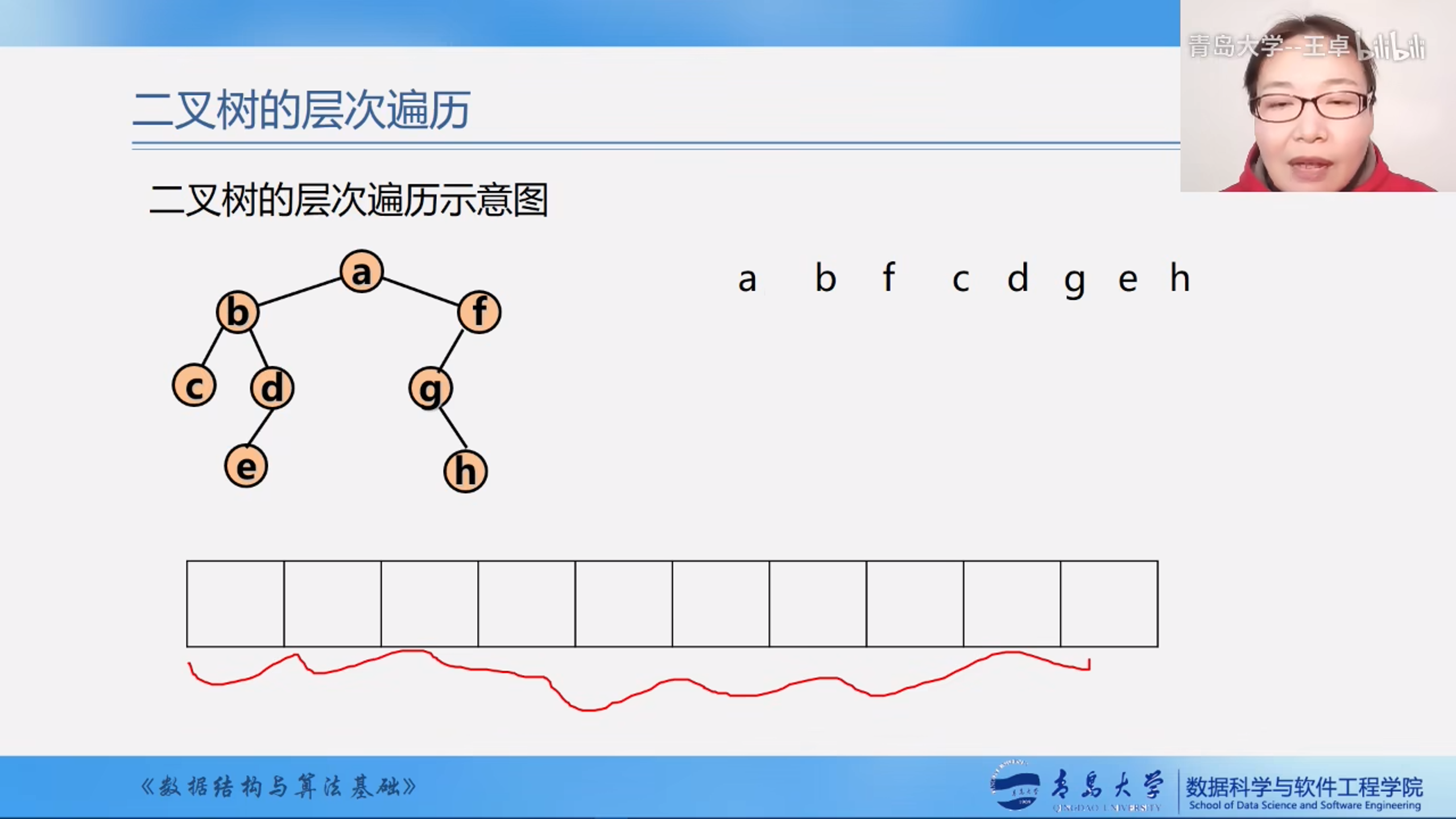
层次遍历需要队列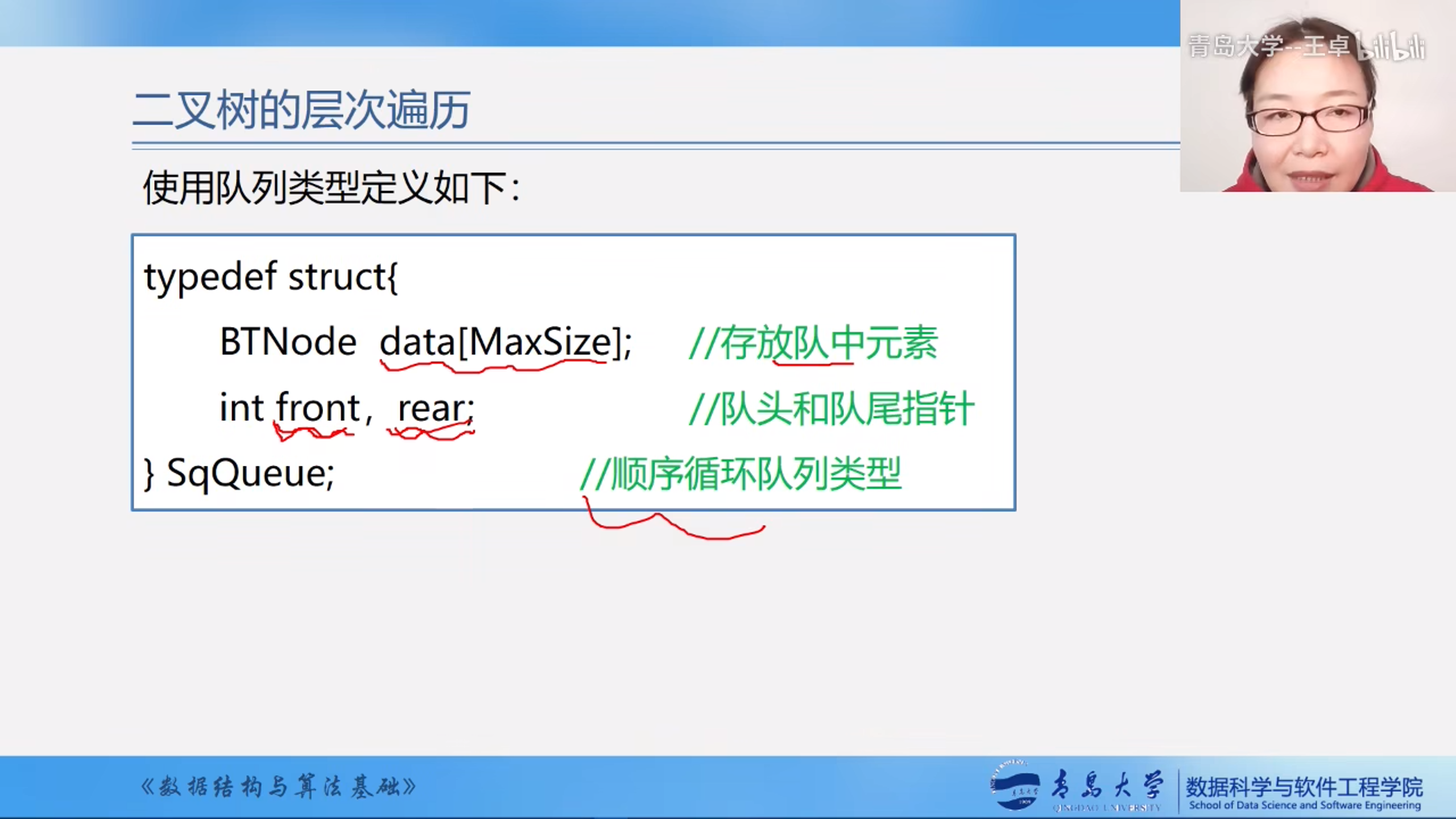
算法的伪代码
C++代码实现
队列使用STL
#include <iostream>
using namespace std;
typedef struct BiNode {
char data;//数据域
struct BiNode *lchild, *rchild; //左孩子右孩子
} BiNode, *BiTree;
/*
前序建立二叉树
*/
void CreateBitree(BiTree &T) {
char ch;
cin >> ch;
if (ch == '#') {
T = NULL; //指针指向空
} else
{
T = new BiNode; //建立一个新结点
T->data = ch; //给新结点赋值
CreateBitree(T->lchild);//创建左孩子
CreateBitree(T->rchild);//创建右孩子
}
}
/*
二叉树的层次遍历算法
*/
void LevelOrder(BiTree T) {
queue <BiTree> q;//生成一个队列
q.push(T);//根结点入队
while (!q.empty()) {//队列不为空就循环
BiTree p = q.front(); //取出队头
cout << p->data; //打印队尾指针指向的结点的数据域
q.pop();//元素出队
if (p->lchild != NULL) { //左孩子入队
q.push(p->lchild);
}
if (p->rchild != NULL) { //右孩子入队
q.push(p->rchild);
}
}
}
signed main () {
BiTree root = NULL;
CreateBitree(root);
cout << "正在进行层次遍历\n";
LevelOrder(root);
cout << '\n';
return 0;
}
/*
abd##eg###cf###
abcdefg
*/
/*
xnl##i##u##
xnuli
*/
二叉树遍历算法分析
前/中/后序遍历算法
可以发现这三种遍历算法只有一行代码,也就是输出结点数据域的位置不同
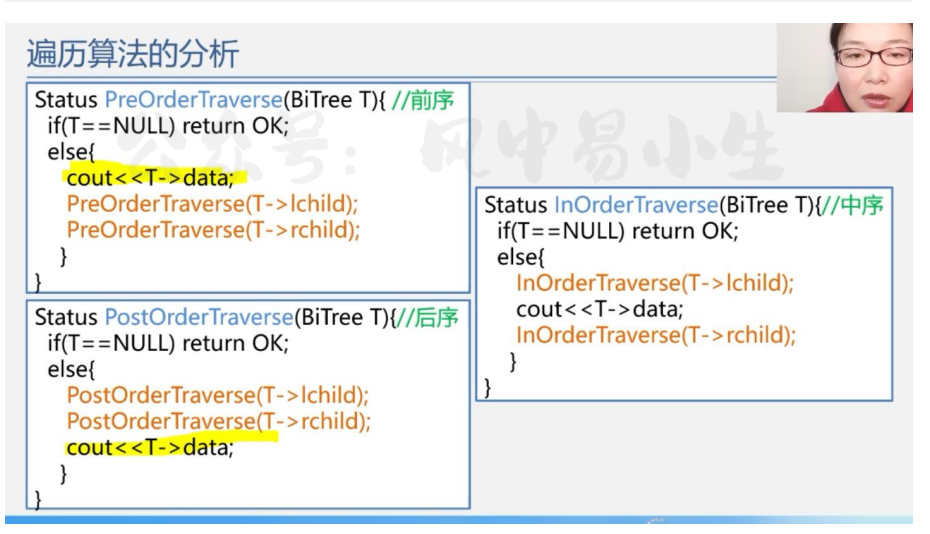
- 前序遍历是先输出数据域再递归到左孩子和右孩子
- 中序遍历是先递归到左孩子等返回的时候输出数据域再递归到右孩子
- 后序遍历是指先递归到左孩子,然后递归到右孩子,最后返回的时候输出数据域
很明显这三种算法的遍历顺序是相同的,只是访问到每个根节点时打印该结点的数据域的时机不同
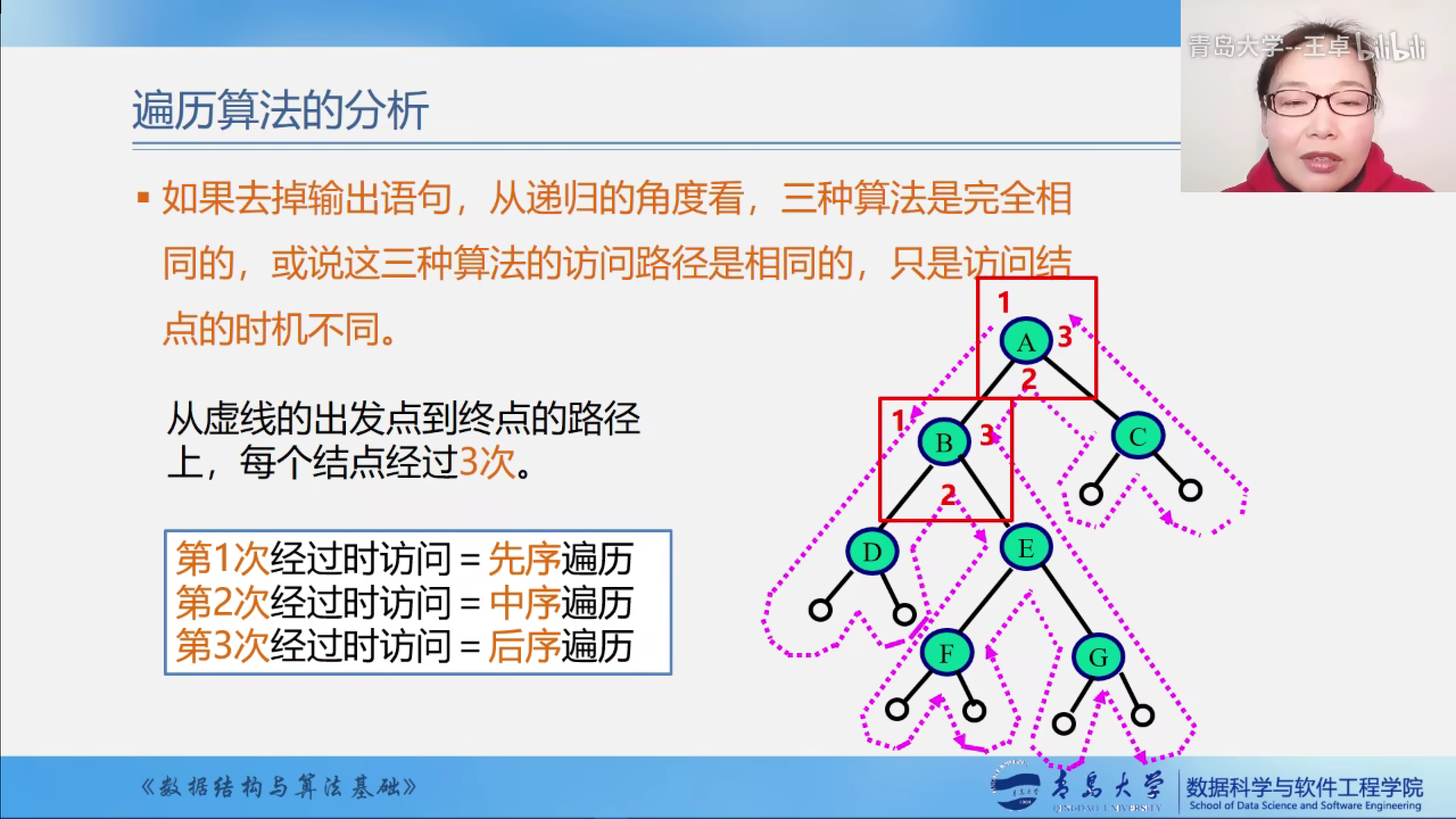
遍历算法的时空复杂度
1.时间为O(n)
2.空间为O(n)
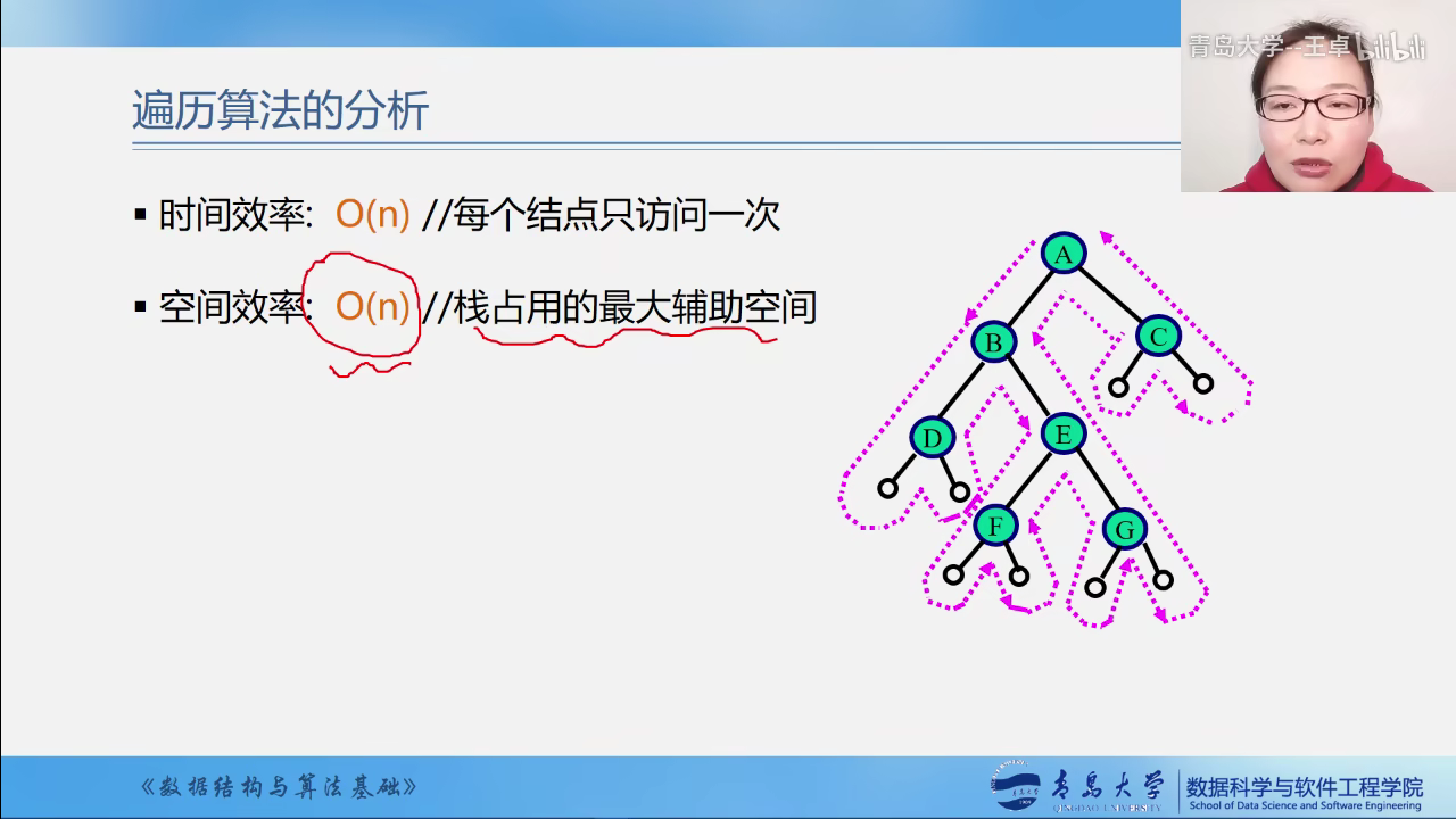
由已知序列求二叉树的原序列
这是一个非常经典的题目,一般是已经知道二叉树的先序遍历和二叉树的中序遍历求二叉树的后续遍历,或者是已经知道二叉树的后续遍历和二叉树的中序遍历来求出二叉树的先序遍历.
先由先序序列确定根,然后再由中序序列确定左右子树
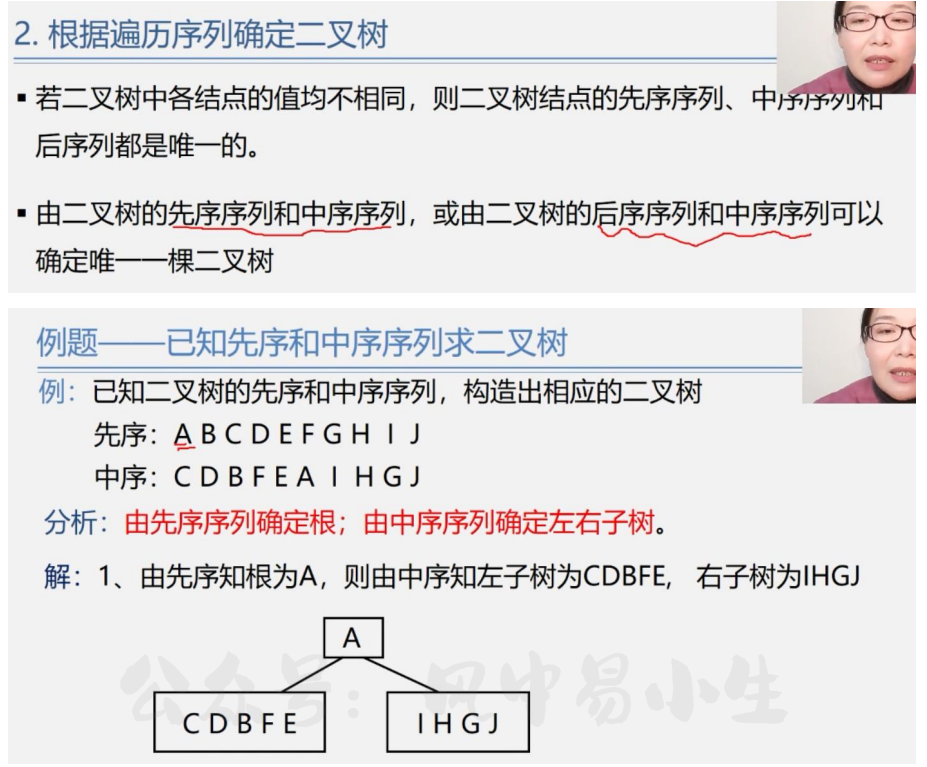
先使用先序遍历找到根是哪个,然后使用中序遍历划分左右子树就可以构建出完整的二叉树了.
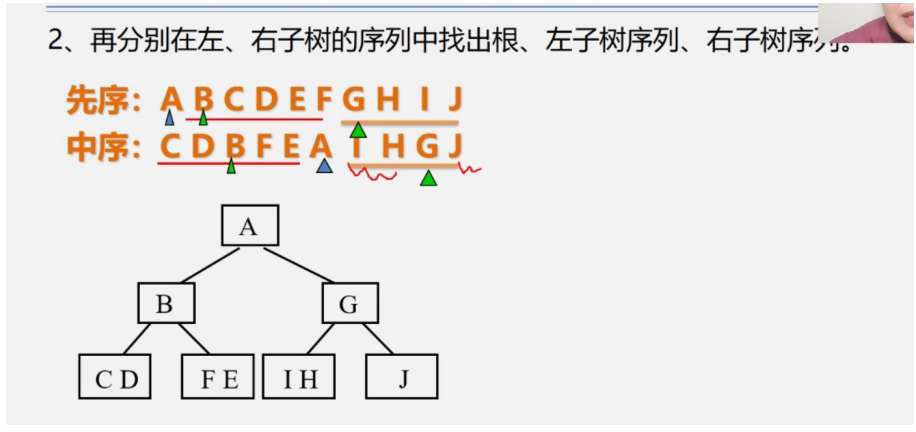
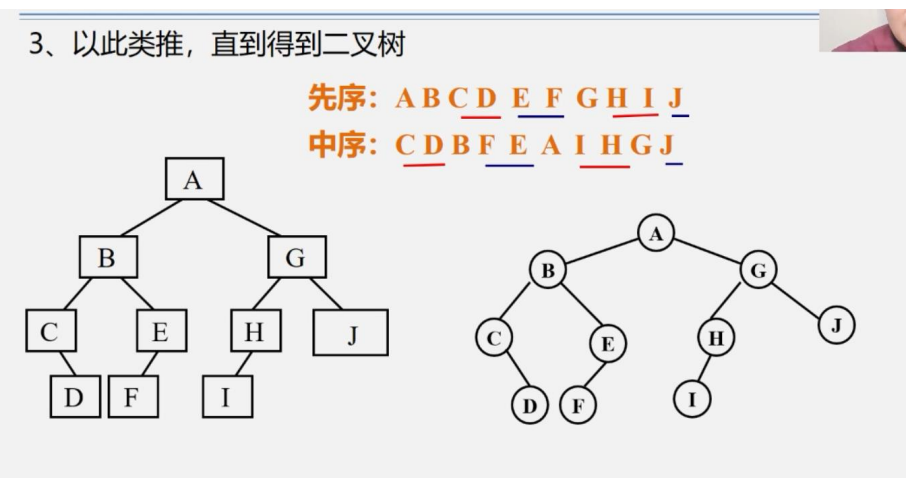
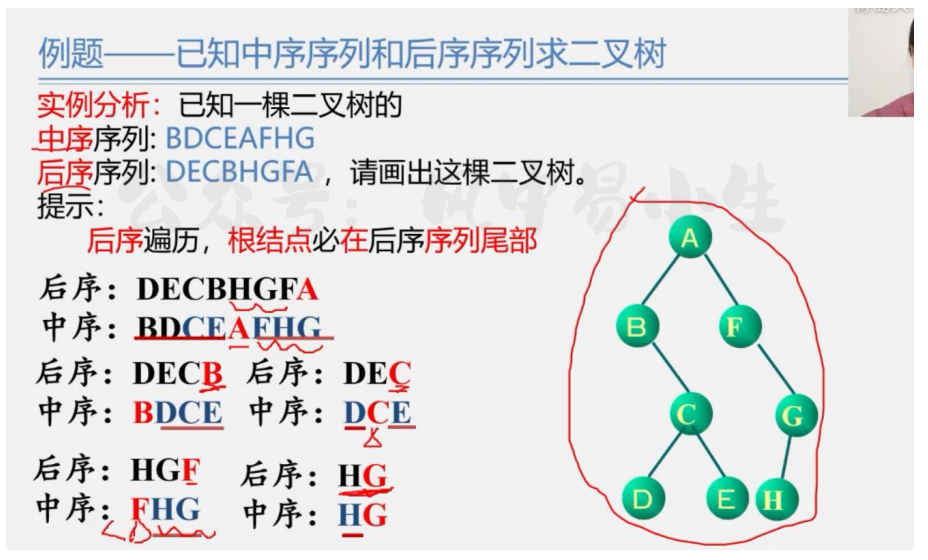
已经知道中序序列和后续序列求二叉树
后序遍历的时候根一定在后续序列的尾部
我们用后续序列从后面向前构建二叉树,然后使用中序遍历划分左右区间.
二叉树的操作
没有什么好说的下面的各种操作要去完整的可以执行的代码进行实现.
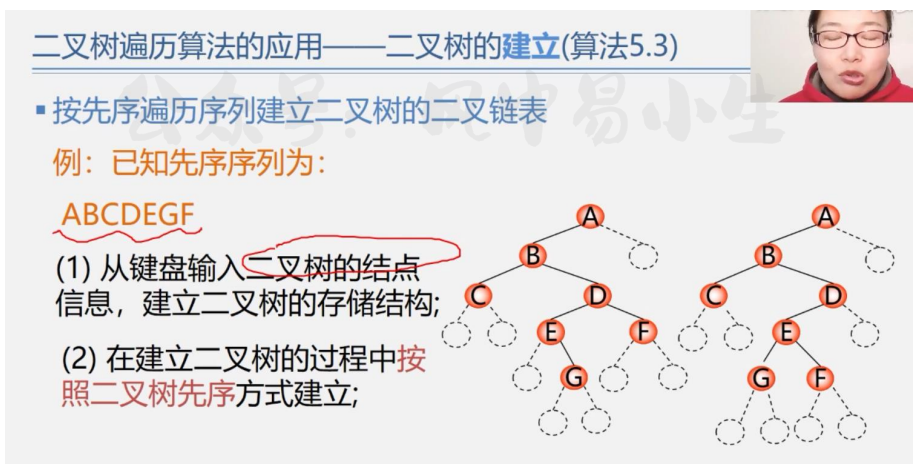
二叉树的建立
二叉树的复制
如果是空树,递归结束
否则, 申请新结点的空间,复制根结点
- 递归复制左子树
- 递归复制右子树
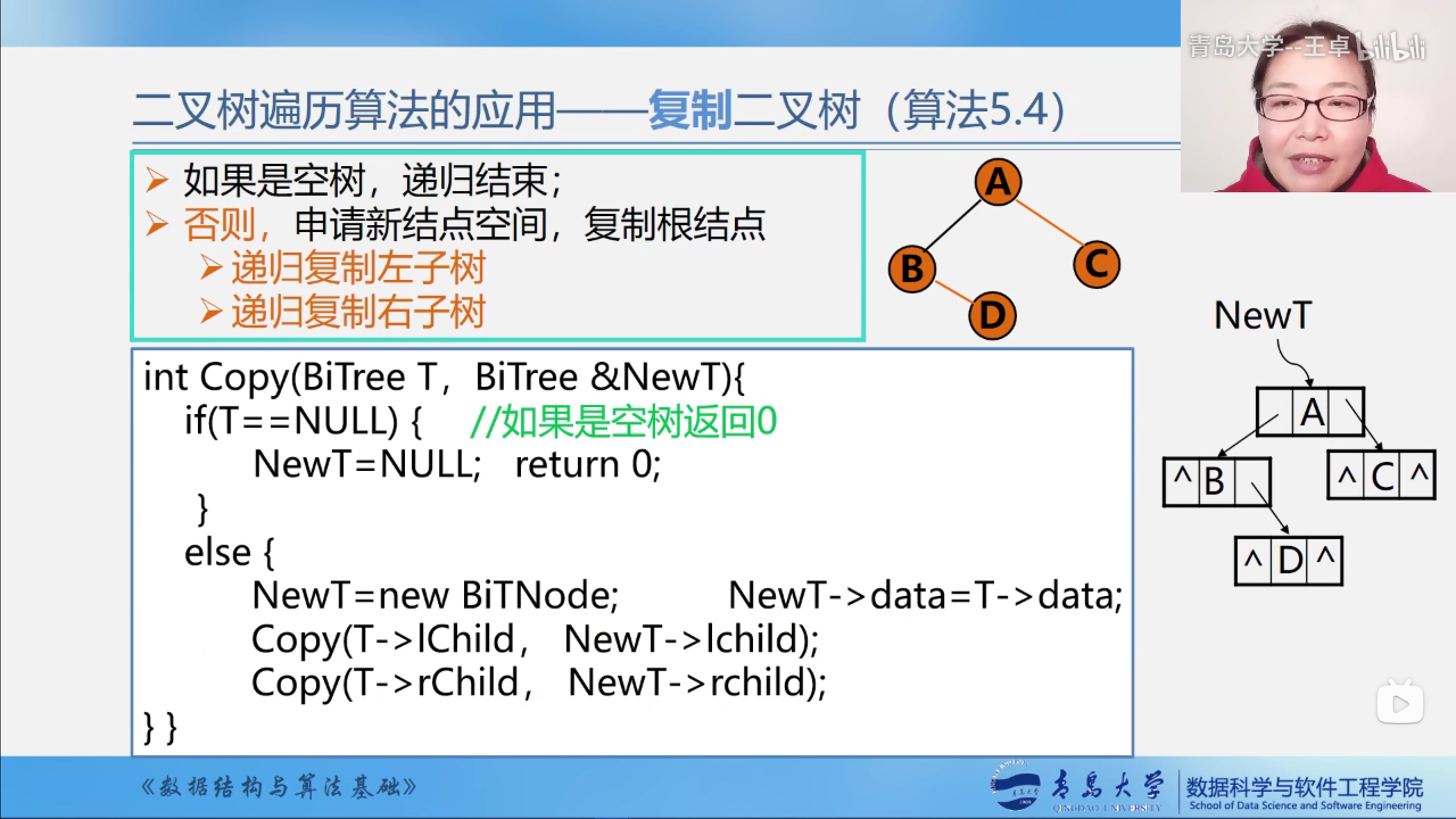
代码实现
#include <iostream>
using namespace std;
typedef struct BiNode {
char data;
struct BiNode* lchild, *rchild;
} BiNode, *BiTree;
void CreateBitree(BiTree &T) {
char ch;
cin >> ch;
if (ch != ',') {
T = new BiNode; //创建一个新结点
T->data = ch;
CreateBitree(T->lchild);
CreateBitree(T->rchild);
} else {
T = NULL;
return;
}
}
/*
二叉树复制函数
需要两个二叉树的根结点
*/
void copyBiTree(BiTree T, BiTree &NewT) {
if (T == NULL) { //如果旧树的地址只为空
NewT = NULL; //那么新树的地址值也为空
} else {
NewT = new BiNode; //创建一个新结点
NewT->data = T->data; //将旧树的值域赋值给新树
copyBiTree(T->lchild, NewT->lchild); //递归复制左子树
copyBiTree(T->rchild, NewT->rchild); //递归复制右子树
}
}
void DLR(BiTree T) {
if (T != NULL) {
cout << T->data;
DLR(T->lchild);
DLR(T->rchild);
} else {
return;
}
}
int main () {
BiTree root = NULL;
CreateBitree(root);
DLR(root);
cout << '\n';
BiTree Newroot = NULL;
copyBiTree(root, Newroot);
DLR(Newroot);
return 0;
}
计算二叉树的深度
如果是空树,则深度为0;
否则,递归计算左子树的深度记为m,递归计算右子树的深度记为n,二叉树的深度则为m与n的较大者加1
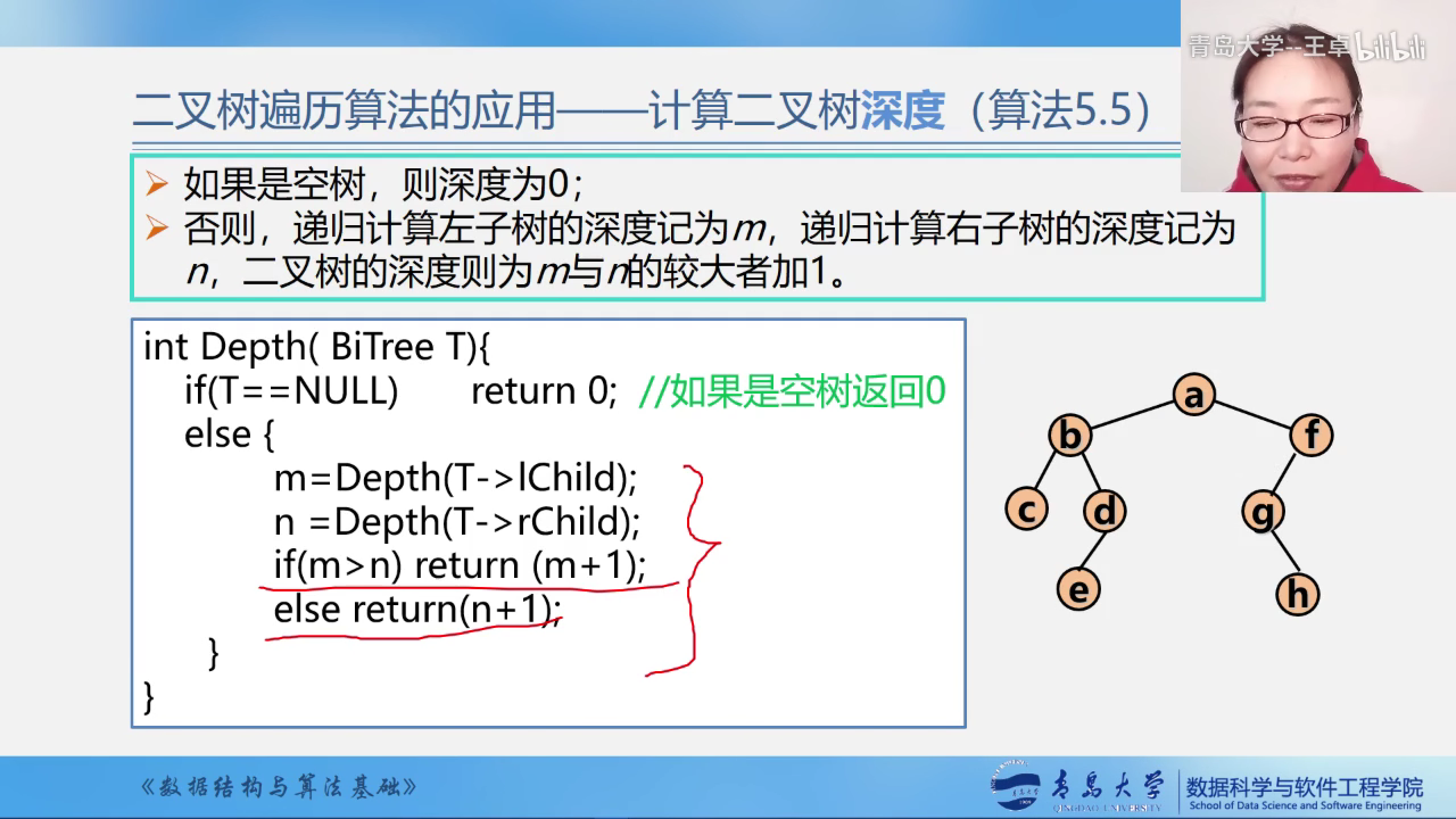
代码示例
#include <iostream>
using namespace std;
typedef struct BiNode {
char data;
struct BiNode* lchild, *rchild;
} BiNode, *BiTree;
void CreateBitree(BiTree &T) {
char ch;
cin >> ch;
if (ch != ',') {
T = new BiNode; //创建一个新结点
T->data = ch;
CreateBitree(T->lchild);
CreateBitree(T->rchild);
} else {
T = NULL;
return;
}
}
/*
二叉树深度计算函数
返回值为二叉树的深度
*/
int Depth(BiTree T) {
int m = 0, n = 0; //m用来记录左子树的深度,n用来记录右子树的深度
if (T == NULL) {
return 0;//空树的返回值为0
} else {
m = Depth(T->lchild);//递归计算左子树
n = Depth(T->rchild);//递归计算右子树
if (m > n) {
return m + 1;//取m,n的较大值加1
//然后返回
} else {
return n + 1;
}
}
}
void DLR(BiTree T) {
if (T != NULL) {
cout << T->data;
DLR(T->lchild);
DLR(T->rchild);
} else {
return;
}
}
int main () {
BiTree root = NULL;
CreateBitree(root);
DLR(root);
cout << '\n';
cout << Depth(root) << '\n';
return 0;
}
题目链接
AC代码
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>
#include <cstring>
#include <unordered_set>
#include <set>
#include <stack>
#include <map>
#include <cmath>
#include <sstream>
#include <queue>
#define yes cout<<"YES"<<'\n'
#define no cout<<"NO"<<'\n'
using namespace std;
typedef struct BiNode {
char data;
struct BiNode *lchild, *rchild;
} BiNode, *BiTree;
void CreateBiTree(BiTree &T) {
char ch;
cin >> ch;
if (ch != ',') {
T = new BiNode;
T->data = ch;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
} else {
T = NULL;
}
}
void DLR(BiTree T) {
if (T == NULL) {
return;
} else {
cout << T->data;
DLR(T->lchild);
DLR(T->rchild);
}
}
void LDR(BiTree T) {
if (T == NULL) {
return;
} else {
LDR(T->lchild);
cout << T->data;
LDR(T->rchild);
}
}
void LRD(BiTree T) {
if (T == NULL) {
return;
} else {
LRD(T->lchild);
LRD(T->rchild);
cout << T->data;
}
}
int LeadCount(BiTree T) {
if (T == NULL) { //如果是空树返回0
return 0;
} else if (T->lchild == NULL && T->rchild == NULL) {
return 1;
} else {
return LeadCount(T->lchild) + LeadCount(T->rchild);
}
}
int Depth_BiTree(BiTree T) {
int m = 0;
int n = 0;
if (T == NULL) {
return 0;
} else {
m = Depth_BiTree(T->lchild);
n = Depth_BiTree(T->rchild);
}
if (m > n) {
return m + 1;
} else {
return n + 1;
}
}
int main () {
BiTree root = NULL;
CreateBiTree(root);
LDR(root);
cout << '\n';
LRD(root);
cout << '\n';
cout << LeadCount(root) << '\n';
cout << Depth_BiTree(root) << '\n';
return 0;
}
/*
abc##de#g##f###
*/
题目链接
AC代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
int m=0,n=0;
if(root==NULL)
{
return 0;
}
else
{
m=maxDepth(root->left);
n=maxDepth(root->right);
if(m>n)
{
return m+1;
}
else
{
return n+1;
}
}
}
};
计算二叉树的结点总数
如果是空树,则结点的个数为0;
否则,结点个数为:左子树的结点个数+右子树的结点个数再+1,加上的1就是正在遍历的结点本身.
代码实现
#include <iostream>
using namespace std;
typedef struct BiNode {
char data;
struct BiNode *lchild, *rchild;
} BiNode, *BiTree;
void CreateBiTree(BiTree &T) {
char ch;
cin >> ch;
if (ch != '#') {
T = new BiNode;
T->data = ch;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
} else {
T = NULL;
}
}
void DLR(BiTree T) {
if (T == NULL) {
return;
} else {
cout << T->data;
DLR(T->lchild);
DLR(T->rchild);
}
}
int NodeCount(BiTree T) { //计算二叉树的叶子结点总数
if (T == NULL) { //空树结点个数为0
return 0;
} else {
return (NodeCount(T->lchild) + NodeCount(T->rchild)) + 1;
}
}
int main () {
BiTree root = NULL;
CreateBiTree(root);
DLR(root);
printf("\n这个二叉树的结点总数为%d", NodeCount(root));
return 0;
}
/*
abc##de#g##f###
*/
计算二叉树的叶子结点数
如果是空树,则叶子结点个数为0;
否则,为左子树的叶子结点个数+右子树的叶子结点个数.
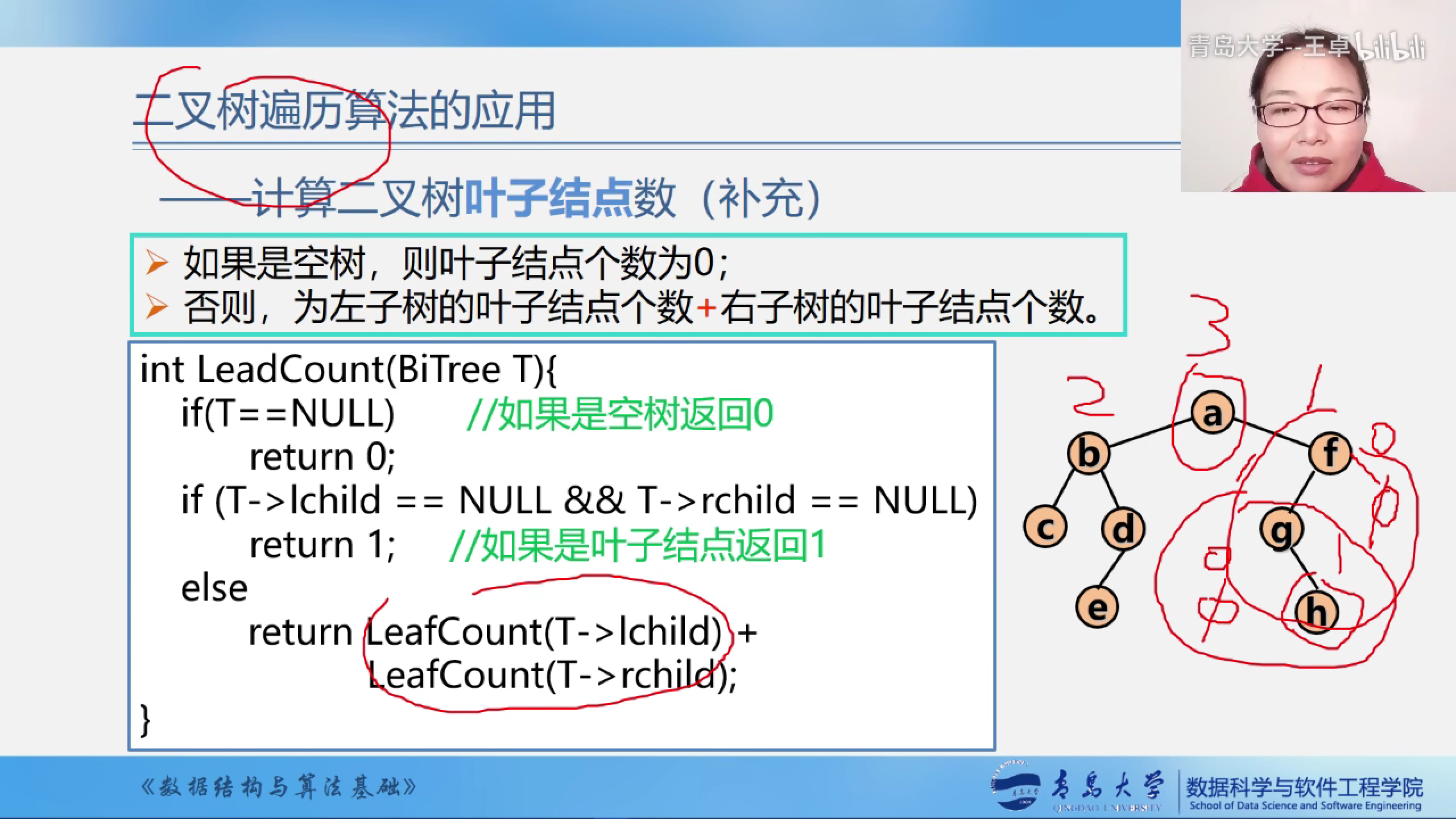
代码实现
#include <iostream>
using namespace std;
typedef struct BiNode {
char data;
struct BiNode *lchild, *rchild;
} BiNode, *BiTree;
void CreateBiTree(BiTree &T) {
char ch;
cin >> ch;
if (ch != '#') {
T = new BiNode;
T->data = ch;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
} else {
T = NULL;
}
}
void DLR(BiTree T) {
if (T == NULL) {
return;
} else {
cout << T->data;
DLR(T->lchild);
DLR(T->rchild);
}
}
int LeadCount(BiTree T) {
if (T == NULL) { //如果是空树返回0
return 0;
} else if (T->lchild == NULL && T->rchild == NULL) {
return 1;
} else {
return LeadCount(T->lchild) + LeadCount(T->rchild);
}
}
int main () {
BiTree root = NULL;
CreateBiTree(root);
DLR(root);
printf("\n这个二叉树的叶子结点总数为%d", LeadCount(root));
return 0;
}
/*
abc##de#g##f###
*/
该题要使用层次遍历
AC代码
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>
#include <cstring>
#include <unordered_set>
#include <set>
#include <stack>
#include <map>
#include <cmath>
#include <sstream>
#include <queue>
using namespace std;
typedef struct BiNode {
char data;
struct BiNode *lchild, *rchild;
} BiNode, *BiTree;
char str[60];
int cnt;
void CreateBiTree(BiTree &T) {
char ch = str[cnt++];
if (ch != ',') {
T = new BiNode;
T->data = ch;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
} else {
T = NULL;
}
}
void DLR(BiTree T) {
if (T == NULL) {
return;
} else {
cout << T->data;
DLR(T->lchild);
DLR(T->rchild);
}
}
void LeadNode(BiTree T) {//层次遍历
queue <BiTree> q;
q.push(T);//先将根结点入队
while (!q.empty()) { //如果队列不空
BiTree f = q.front(); //取出队头
if (f->lchild != NULL) {//队头的左结点不为空,左指针入队
q.push(f->lchild);
}
if (f->rchild != NULL) {//队头的右结点不为空,右指针入队
q.push(f->rchild);
}
if (f->lchild == NULL && f->rchild == NULL) {//如果当前的结点是叶子结点打印当前的data
cout << f->data;
}
q.pop();
}
}
int main () {
while (scanf("%s", str) != EOF) {
cnt = 0;
BiTree root = NULL;
CreateBiTree(root);
LeadNode(root);
cout << '\n';
}
return 0;
}
/*
abc##de#g##f###
*/
