树和二叉树的基本概念

树和二叉树的基本概念

树的定义

树是一个递归的定义了,也就是说树中一个结点和其孩子结点都可以看成一个树.

树有多种表示方式但是我们通常使用第一种递归的定义来表示树结构.

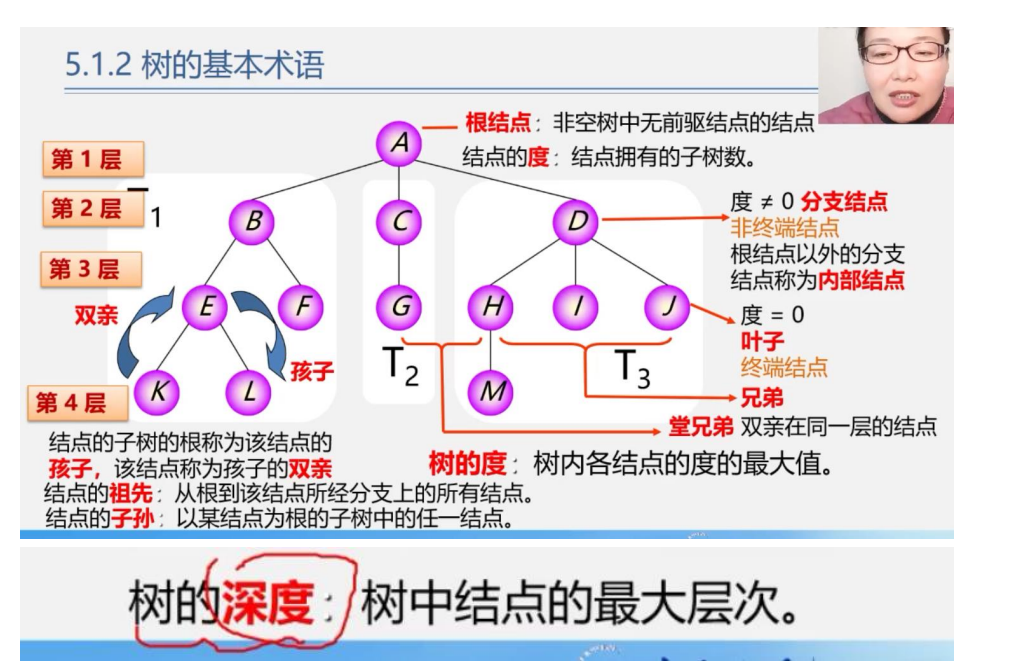
树的基本术语

根结点:非空树中没有前驱结点的结点.

结点的度:结点拥有的子树数,也就是该结点向下直接连接的结点个数.其中如果一个结点的度为0,则该结点为叶子结点,否则为非叶子结点.

树的度:树中结点度的最大值.

树的深度:树中结点的最大层次.

结点的祖先：从根到该结点所经分支上的所有结点。都是该结点的子孙.
结点的子孙：以某结点为根的子树中的任一结点。以该结点形成的树,树中所有的结点都叫做该节点的子孙.

结点的子树的根称为该结点的
孩子，该结点称为孩子的双亲.这是一个双向定义.

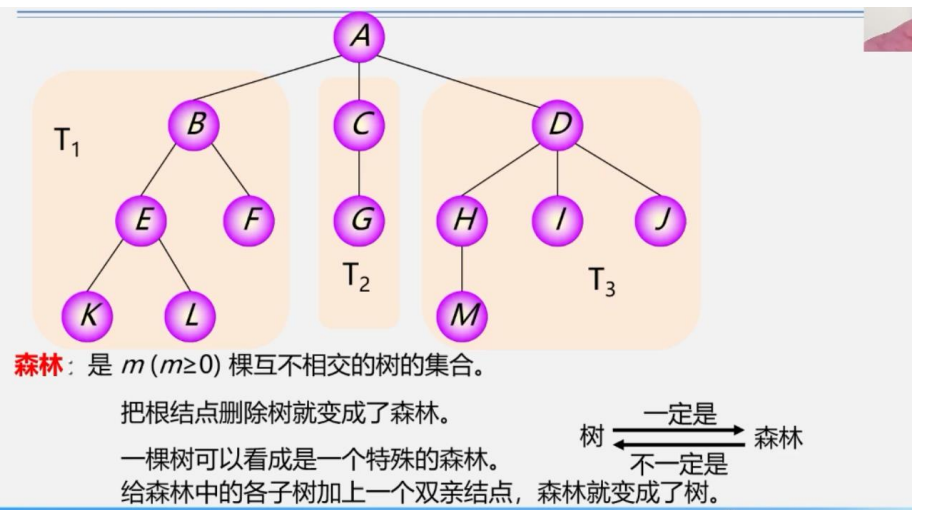
树和森林

树一定是森林,森林不一定是树

将一颗树的根节点删除就可以变成森林,同时一片森林加上一个根结点可以变成一棵树.

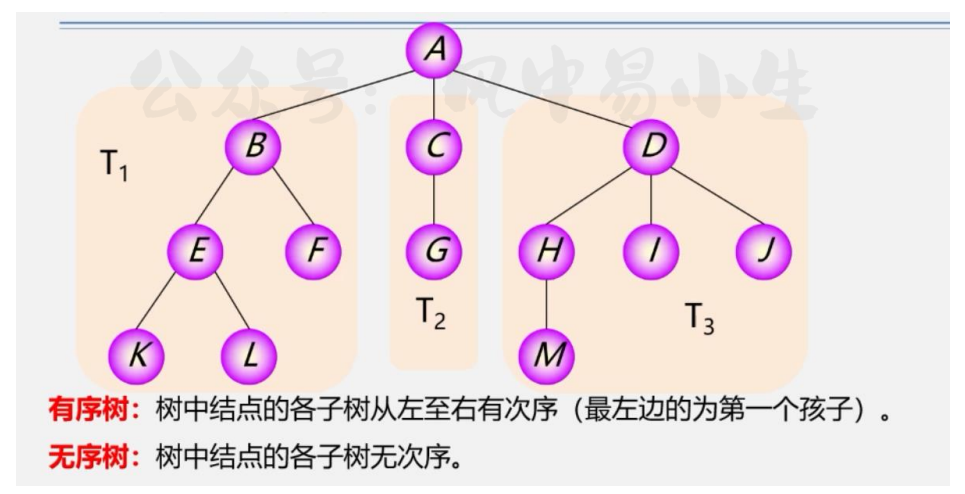
有序树和无序树

如下图,如果我们规定T1,T2,T3必须有序,如果T1,T2,T3交换顺序之后就不是原本的树了,这叫做有序树.

如果我们规定下面的T1,T2,T3交换顺序之后还是这颗树的话,叫做无序树.

树结构

根结点:无双亲结点.

叶子结点:无孩子结点.

其他结点:一个双亲结点多个孩子结点.

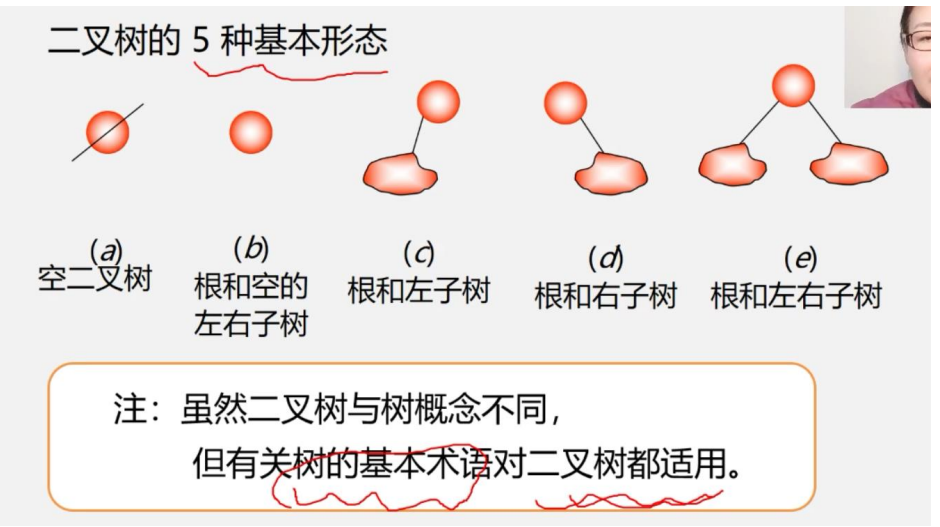
二叉树的定义

一种非常重要的数据结构,我们研究树结构主要研究的就是二叉树.

特点

1.二叉树中不存在结点的度大于2的结点.

2. 二叉树中的左右子树的次序一定不能颠倒

二叉树可以是空集合,二叉树中结点的度可以为0,1,2

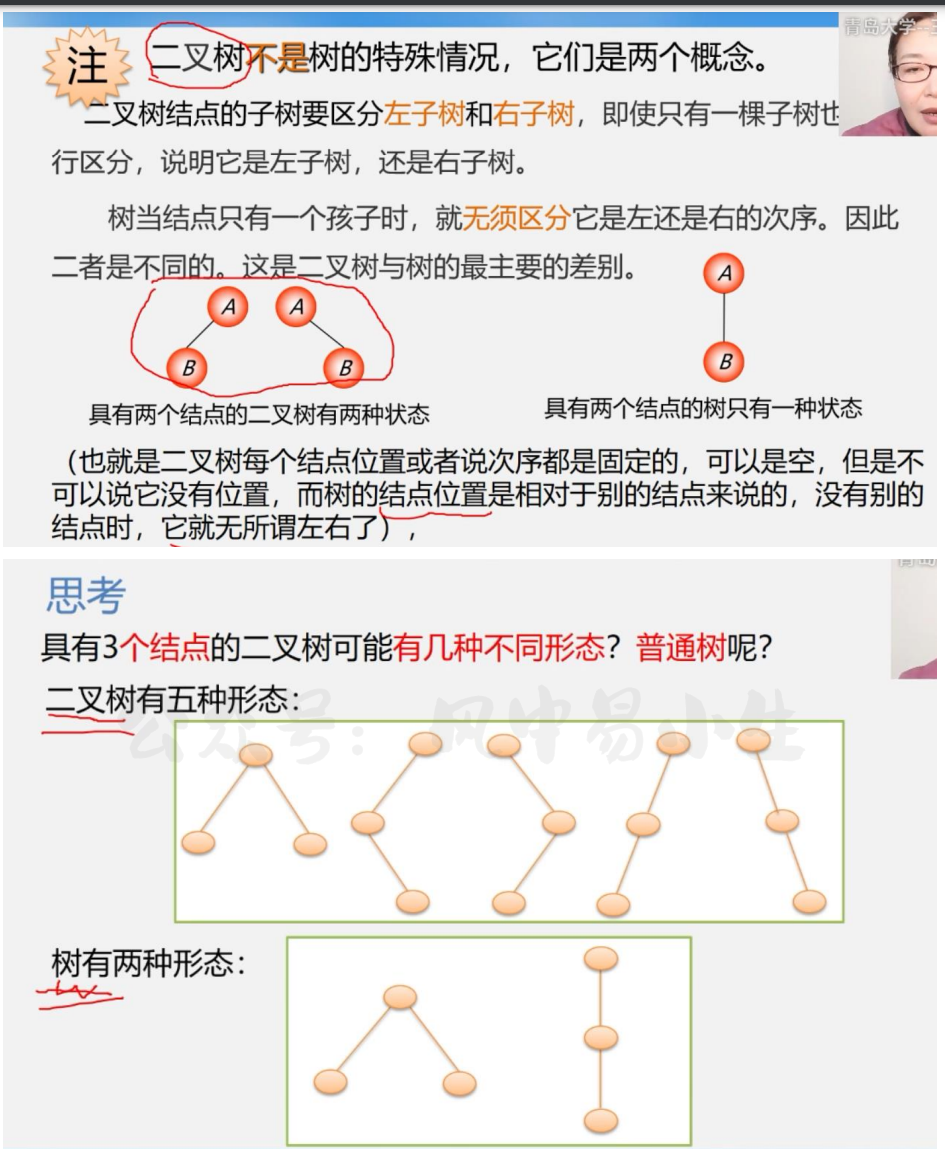
二叉树不是树的特殊情况,它们是两个概念.

就算二叉树只有一个几点还是要区分左右子树的,但是树如果只有一个和结点,就不需要区分子树.

树当结点只有一个孩子时，就无须区分它是左还是右的次序。因此二者是不同的。这是二叉树与树的最主要的差别

二叉树可以解决的问题

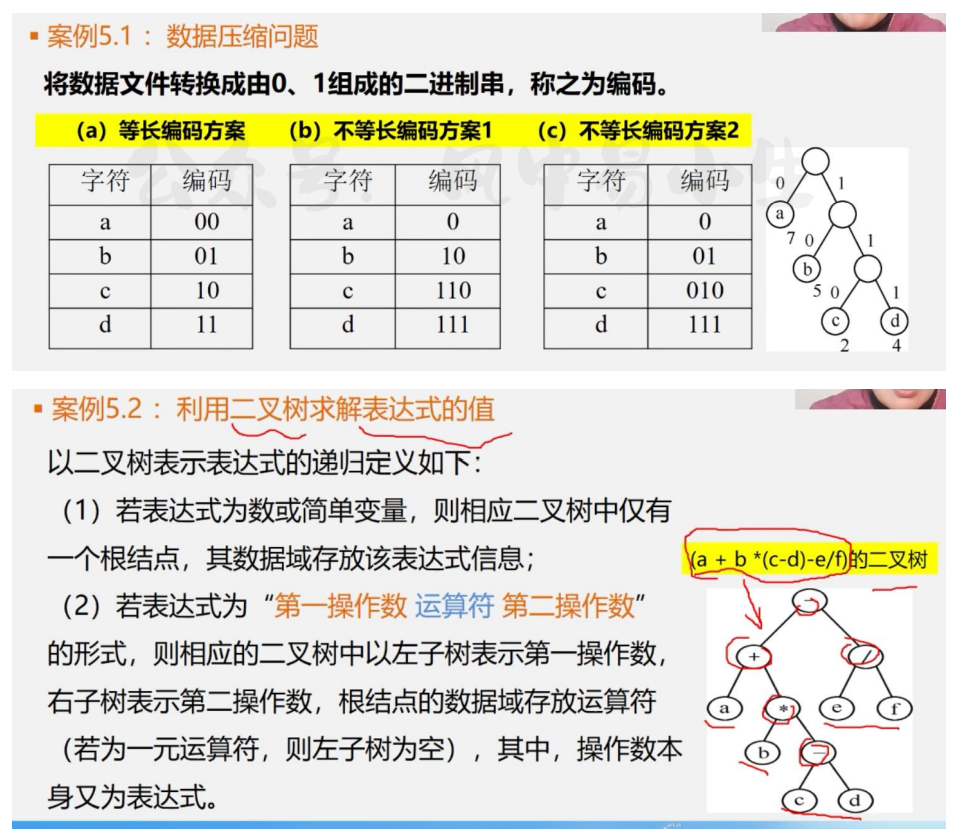
二叉树的抽象数据类型定义

二叉树的性质

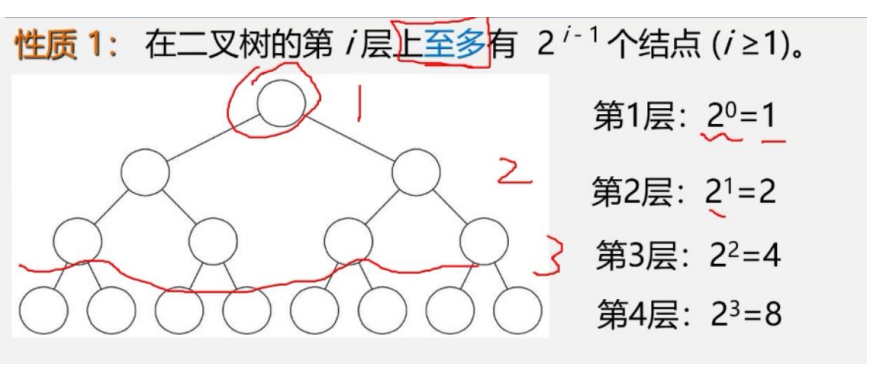
性质1:

在二叉树的第i层上至多有pow(2,i-1)个结点(i≥1).

性质2:

深度为k的二叉树至多有pow(2,k)-1个结点(k≥1)

深度为k时至少有k个结点,此时的二叉树退化为一条链

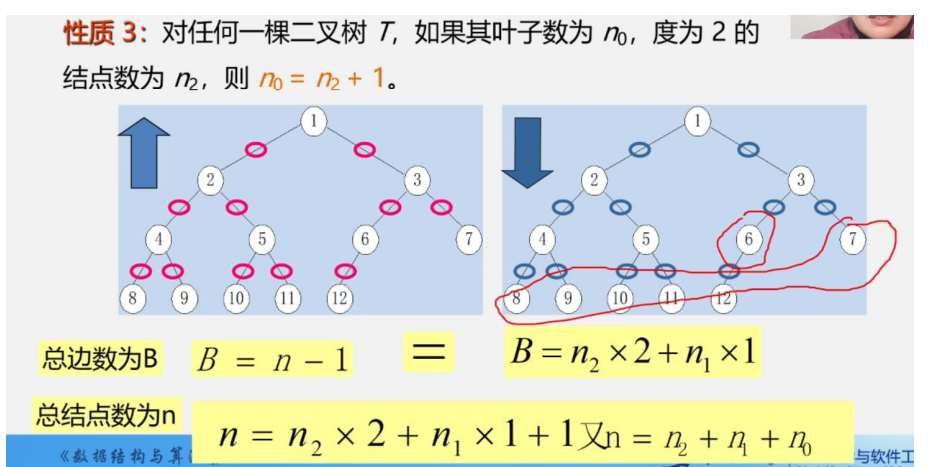
性质3:

对任何一棵二叉树T,如果其叶子数为n0，度为2的
结点数为n2，则n0=n2+1。

记度为0的结点的个数为n0,度为1结点的个数为n1,度为2的结点的个数为n2

证明:从下向上看的话,除了根结点之外其余的每个结点都和双亲之间有一条边.所以有n个结点的二叉树的边数为n-1个.

从上向下看,该二叉树中边的个数为2n2+n1=n-1

将上面的两个条件连接起来为n-1=2n2+n1,又因为n0+n1+n2=n

所以n0+n1+n2-1=2n2+n1

最后n0=n2+1

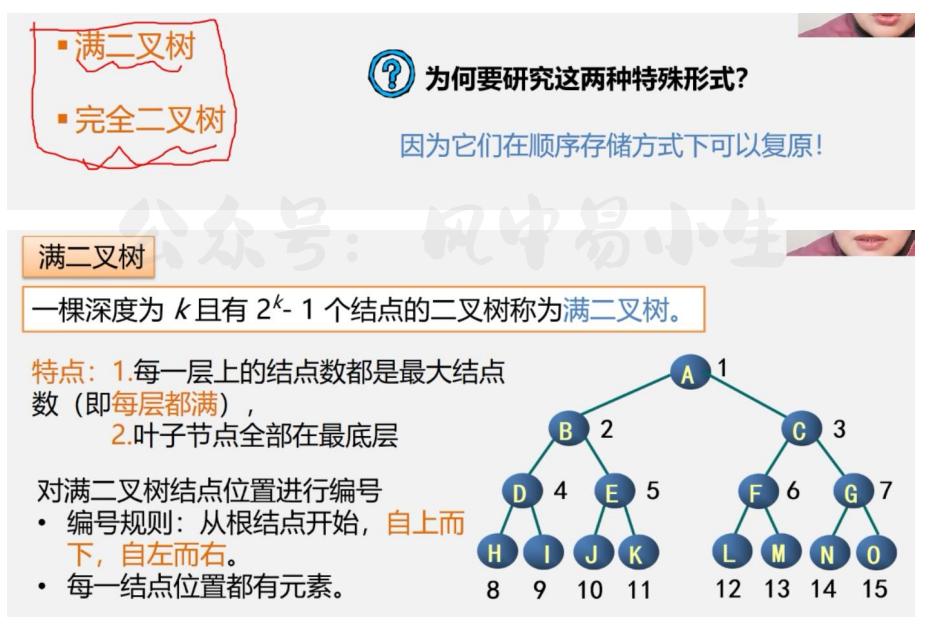
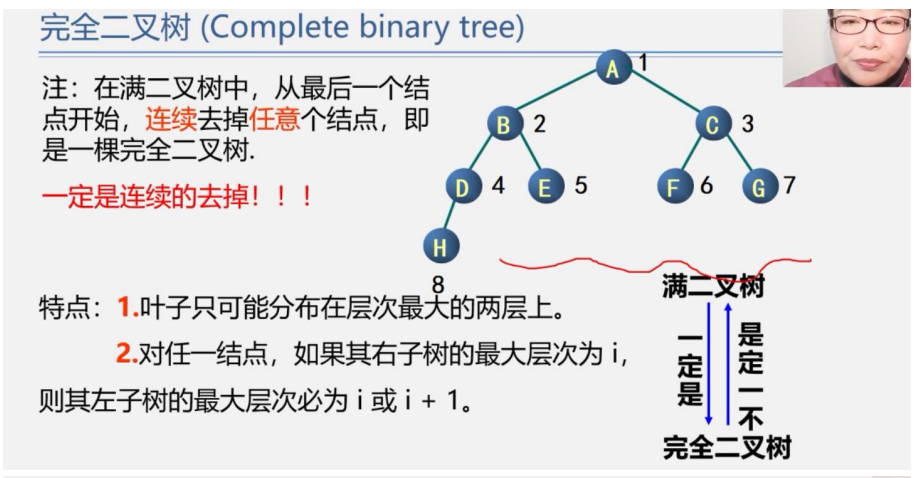
满二叉树

最后一层结点个数数量达到最大的二叉树,并且所有的叶子结点都在最后一层.

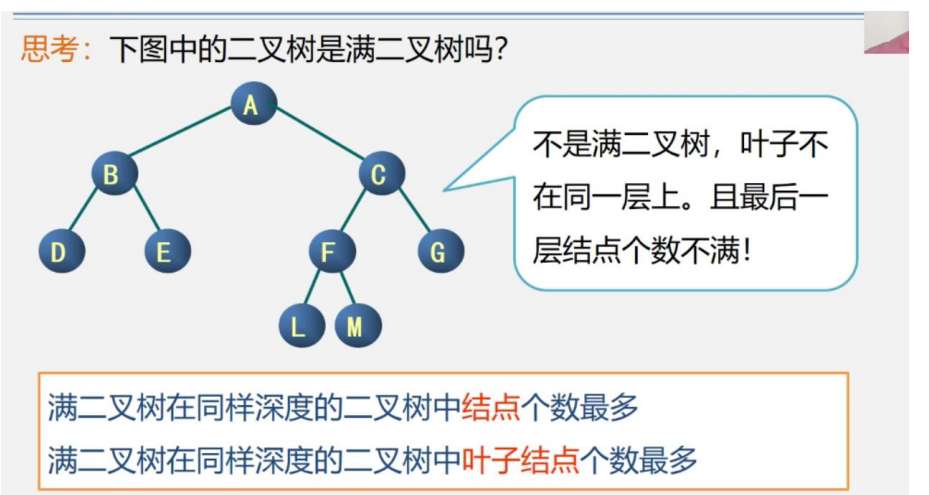
满二叉树在同样深度的二叉树中结点个数最多
满二叉树在同样深度的二叉树中叶子结点个数最多

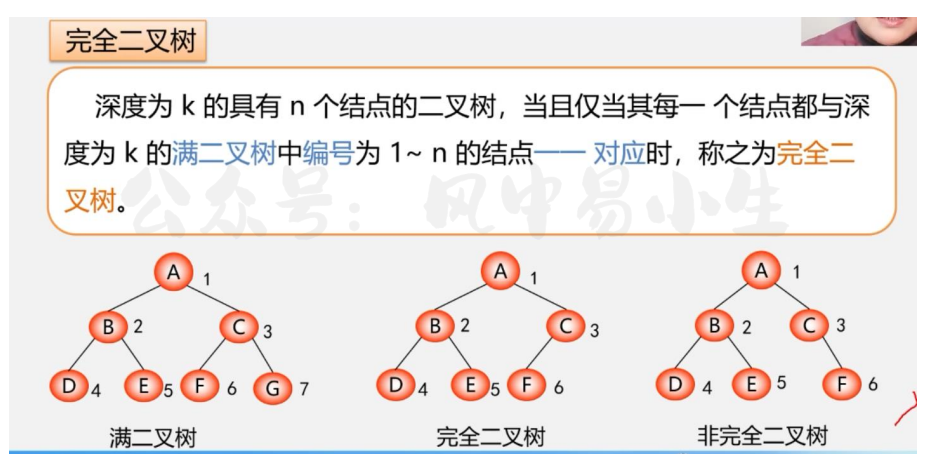
完全二叉树

将该二叉树n个结点进行层次遍历,然后进行编号,使该n个结点与编号1-n都一一对应,.这样的二叉树称之为完全二叉树.

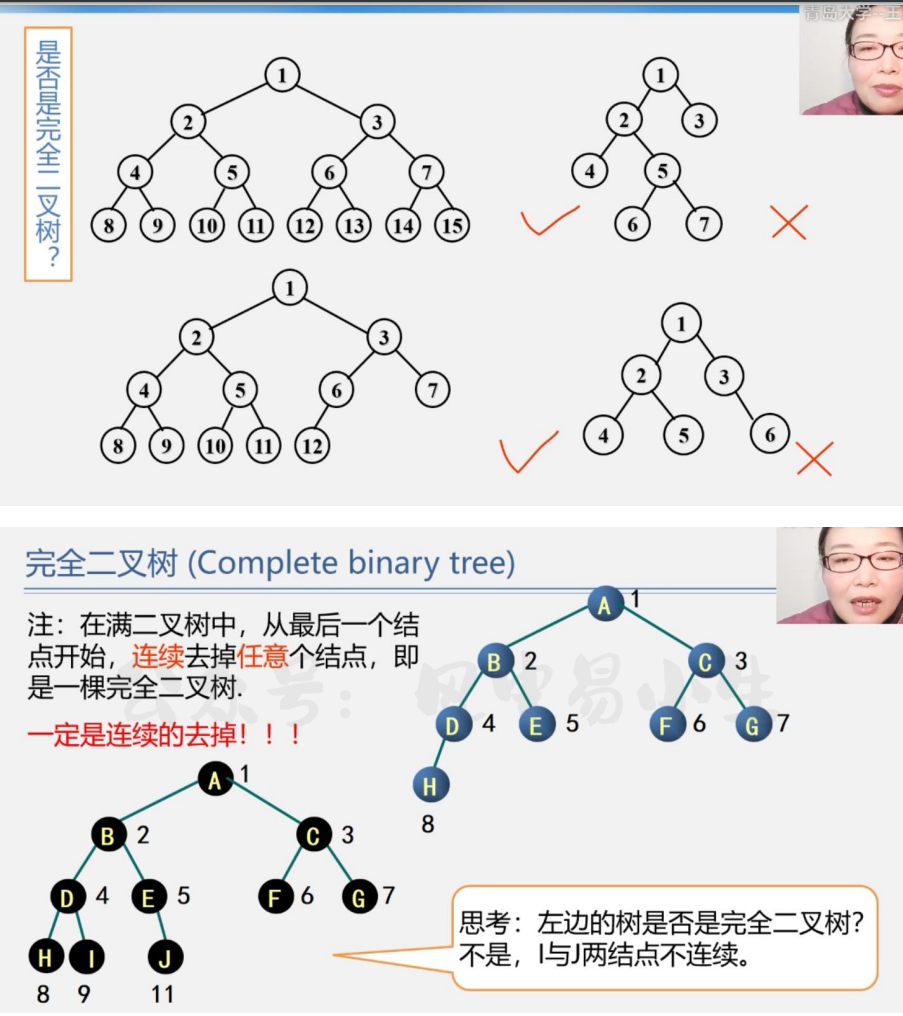
左边的二叉树不是完全二叉树,因为缺少了10号结点,不是连续的.

性质4:

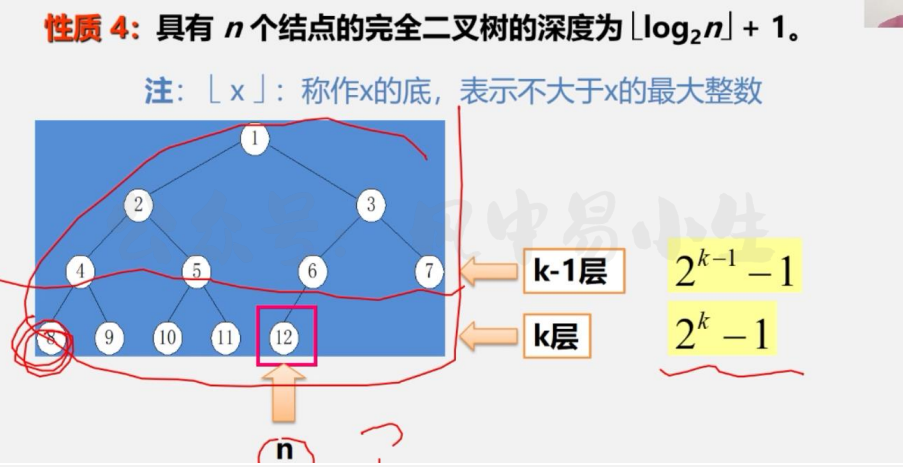
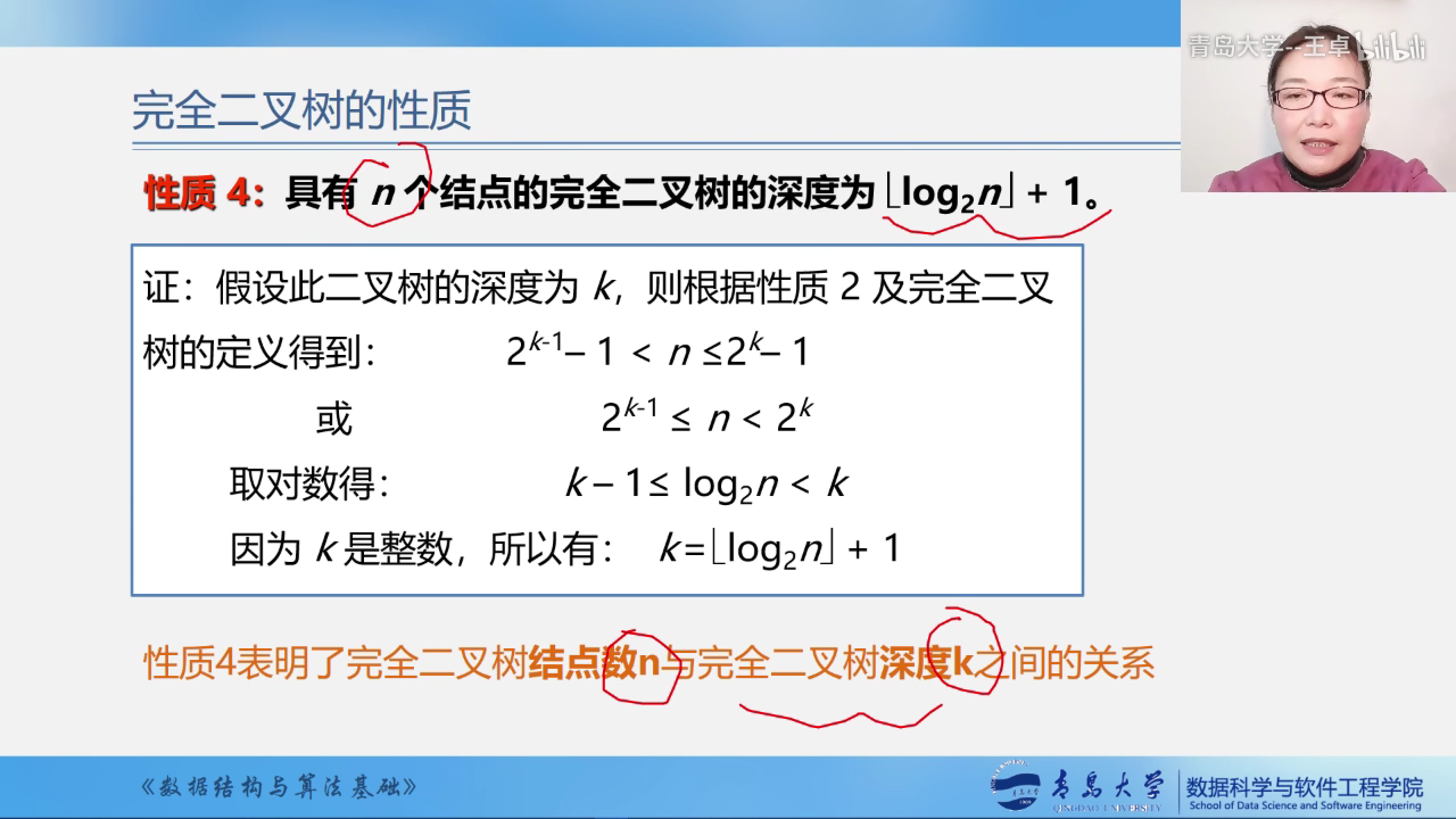
性质4说明完全二叉树结点数n与完全二叉树深度k之间的关系

性质5

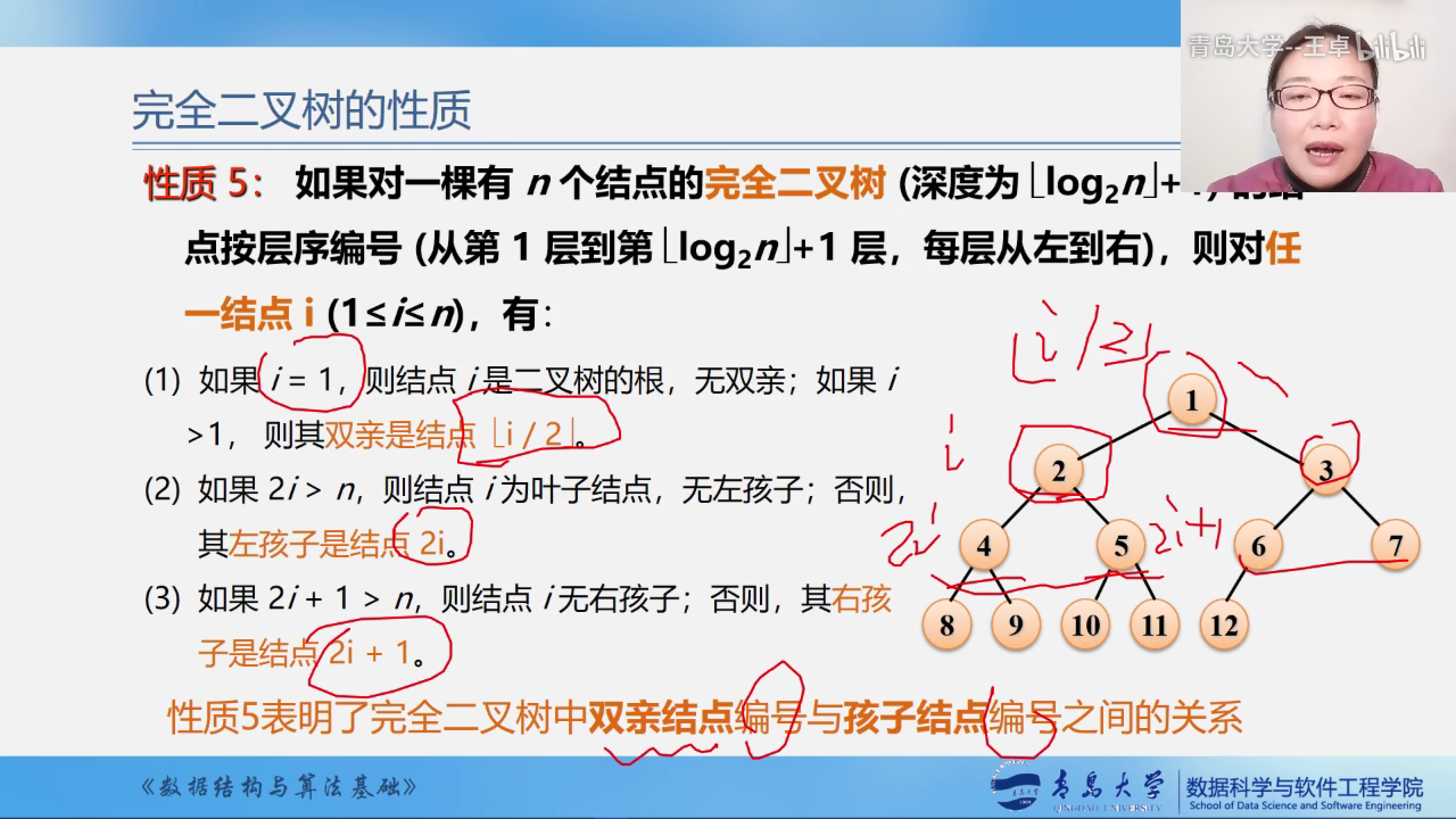
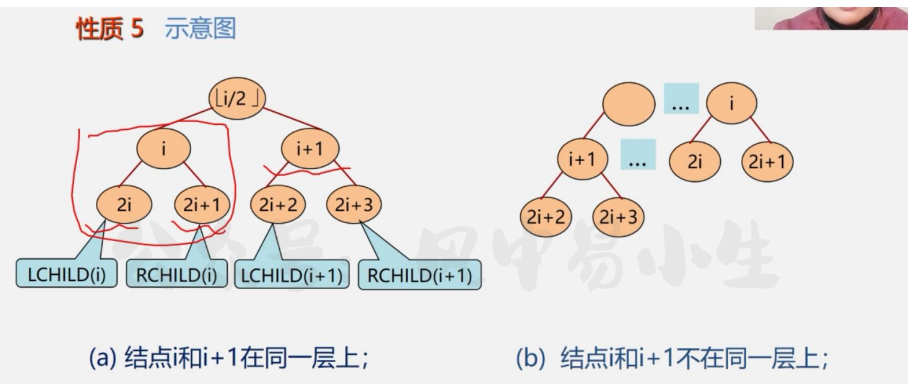
1.即某个结点(i/2)向下取整就是其双亲结点

2.某个结点的2i位置是该结点的左孩子,如果2i<n的话,说明该结点没有左孩子.

3.某个结点的2i+1位置是该结点的右孩子,如果2i+1<n的话,说明该结点没有右孩子.