数据结构--选择排序

数据结构--选择排序

简单选择排序

在待排序的数据中选出最大的(小)的元素放在其最终位置.

简单选择排序的演示

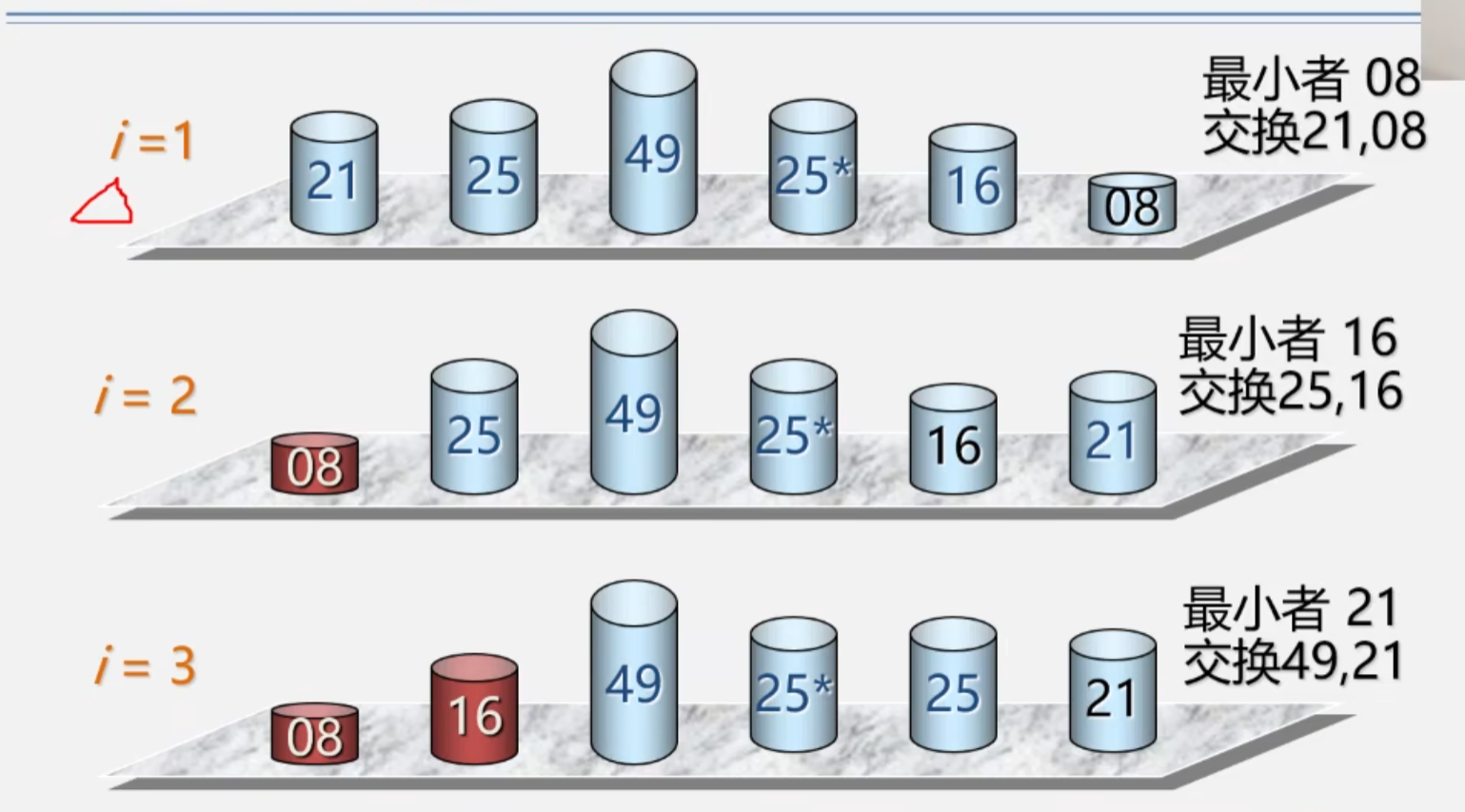
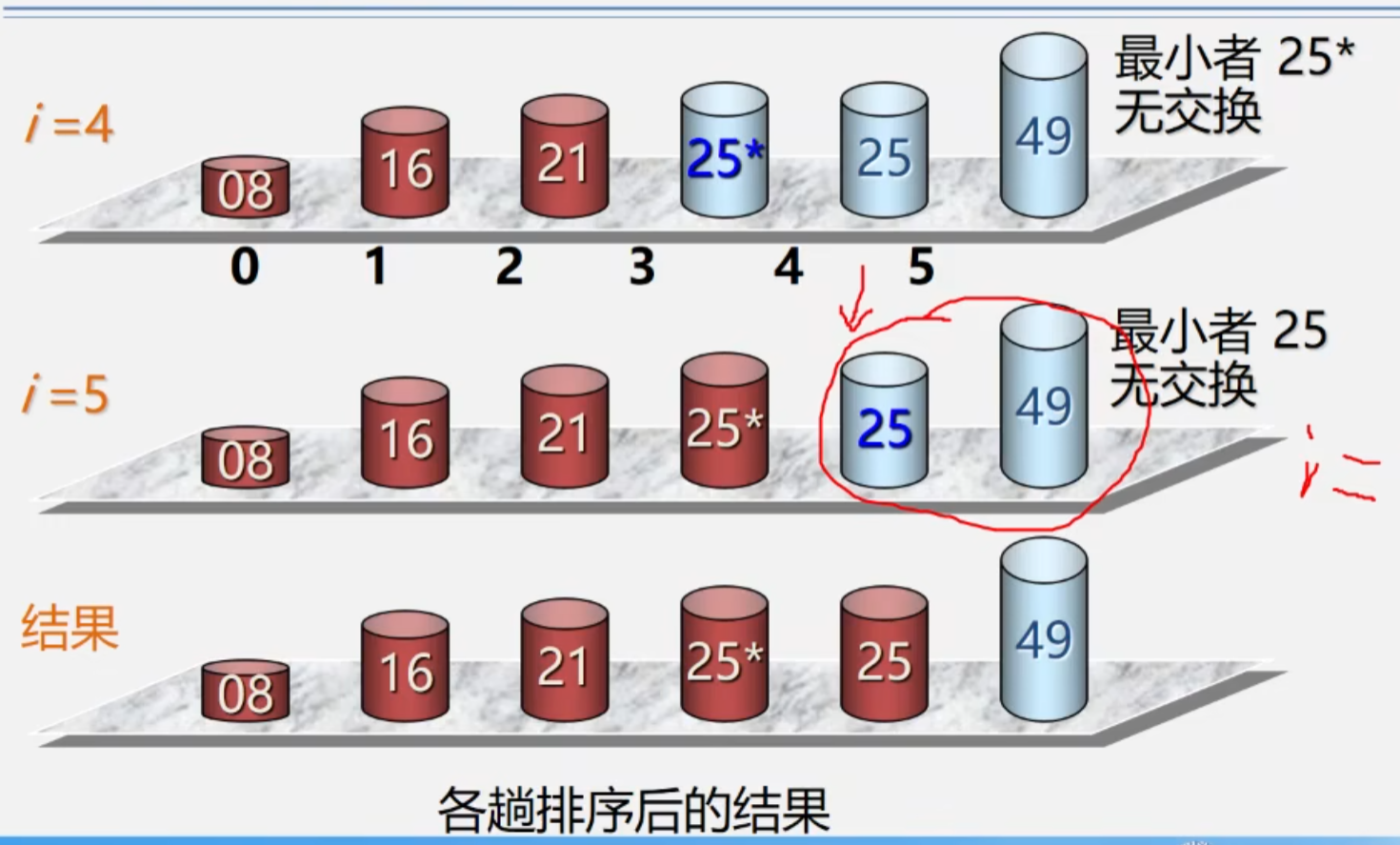
简单选择排序算法

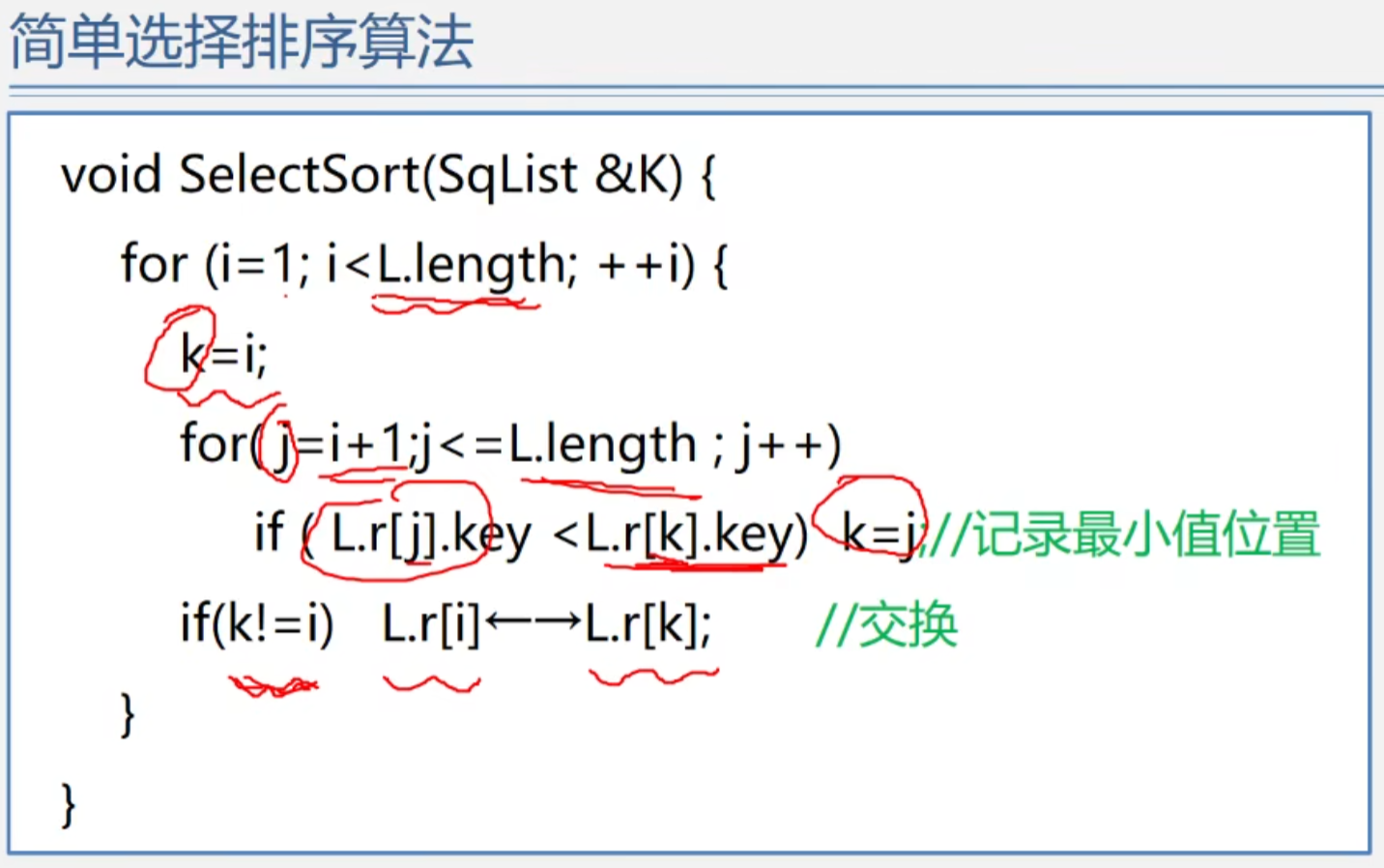
简单选择排序算法分析

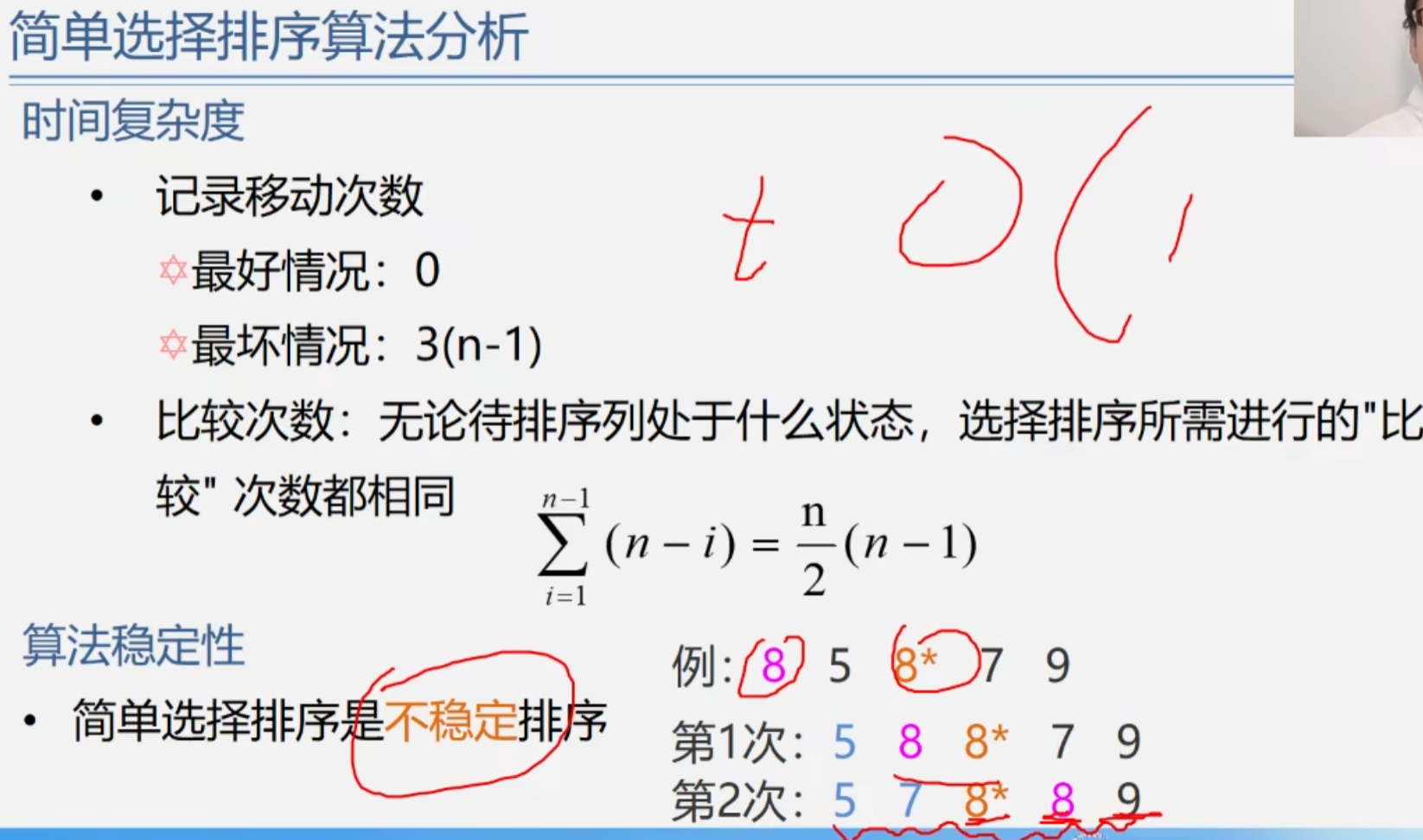
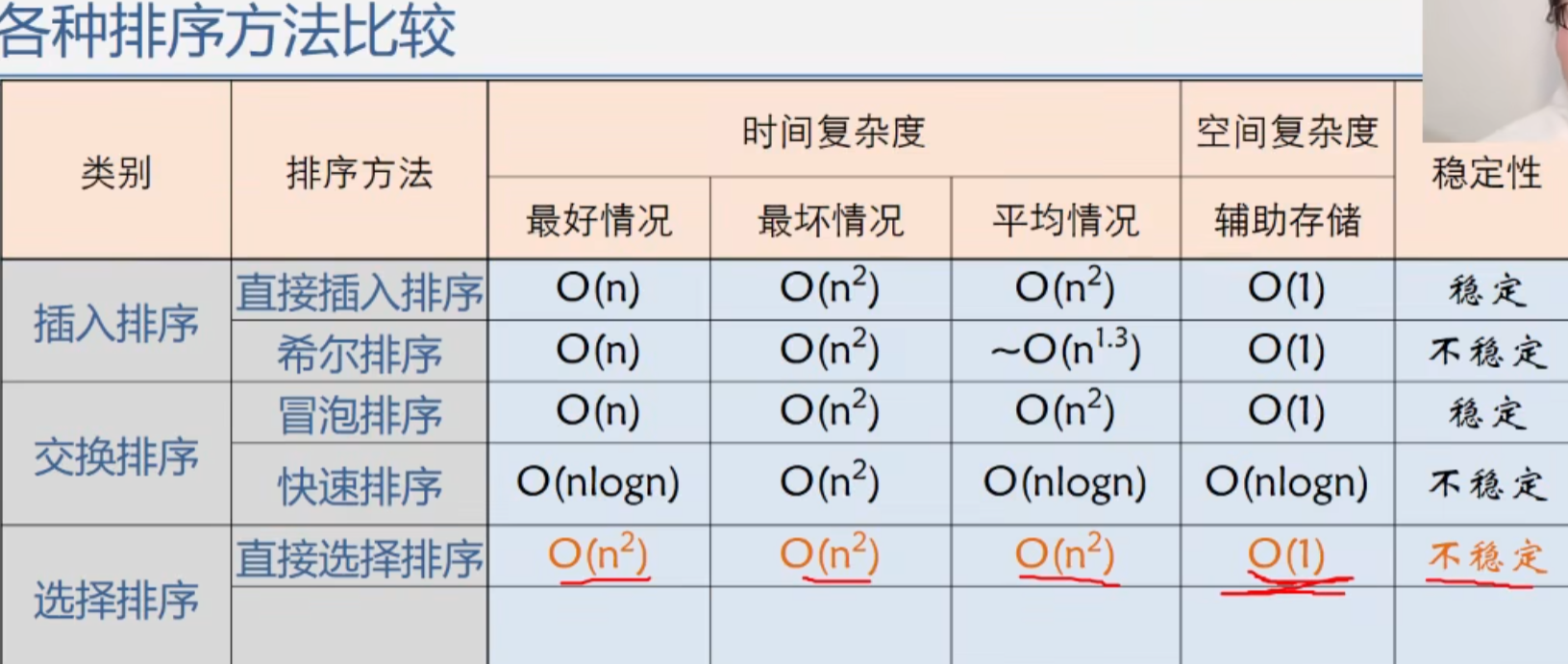
排序方法的比较.

堆排序

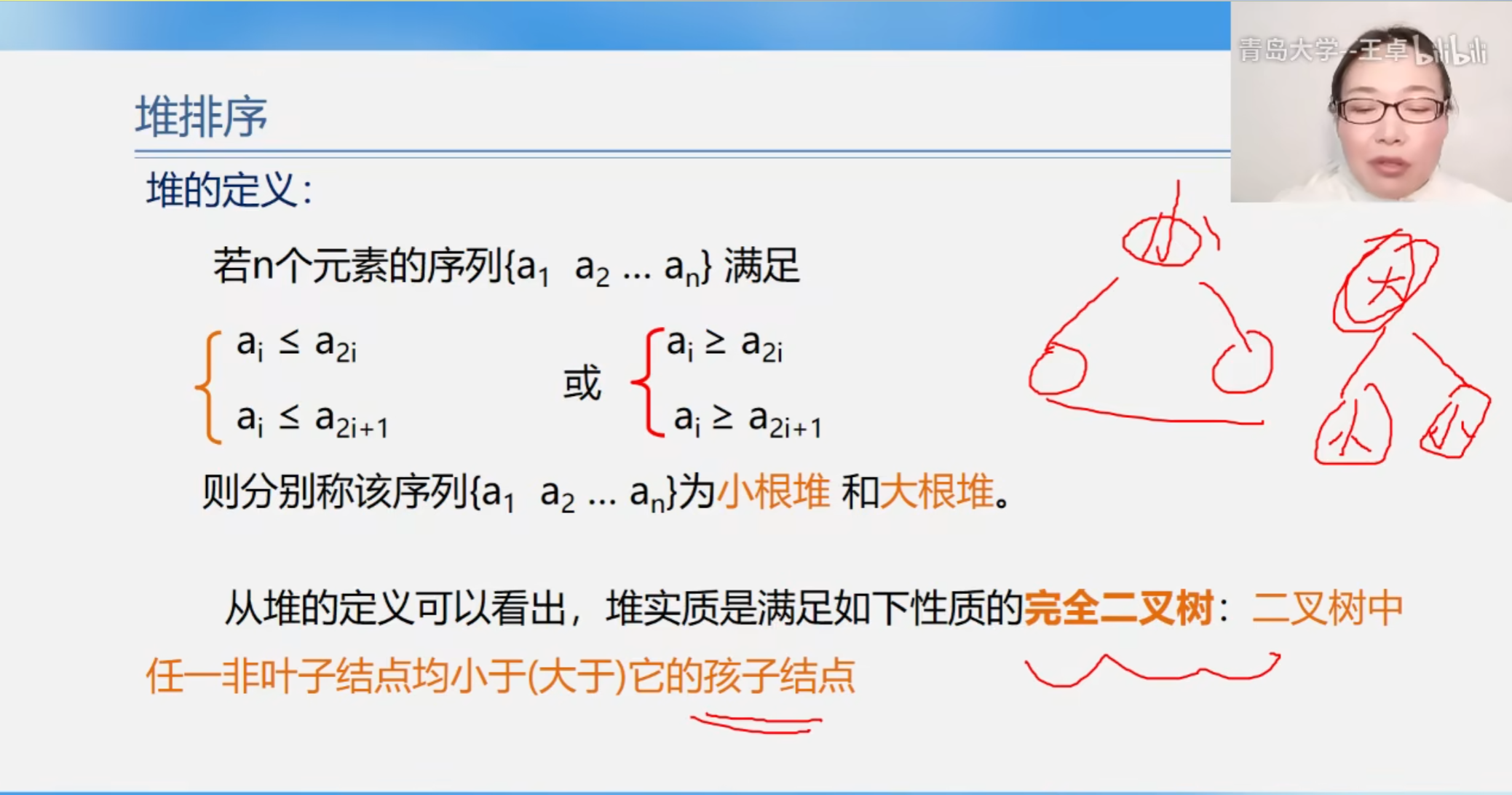
什么是堆?

堆实际上是一个完全二叉树.并且二叉树中任一非叶子结点均小于(大于)它的孩子结点.

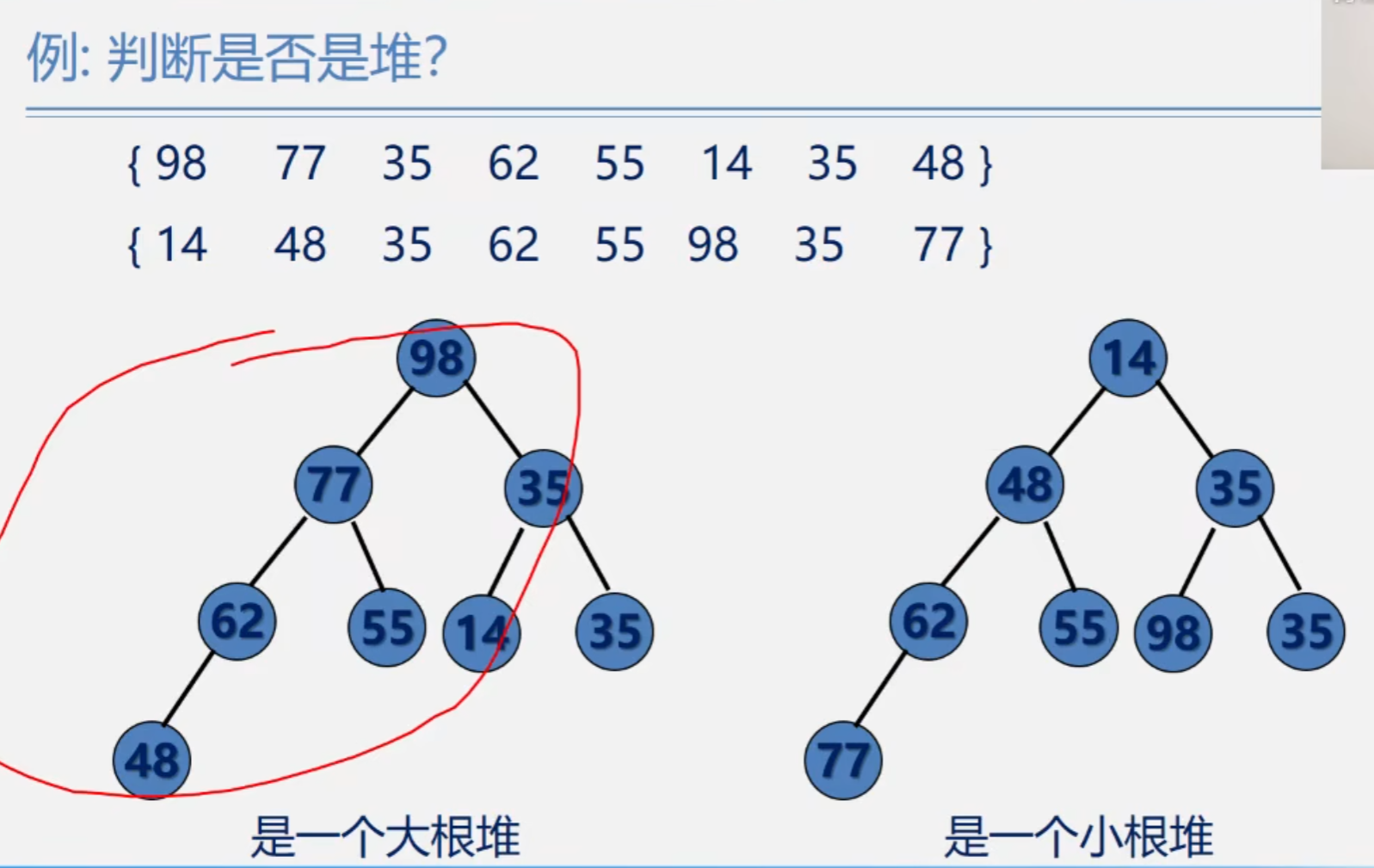
第一个为大根堆

第二个为小根堆

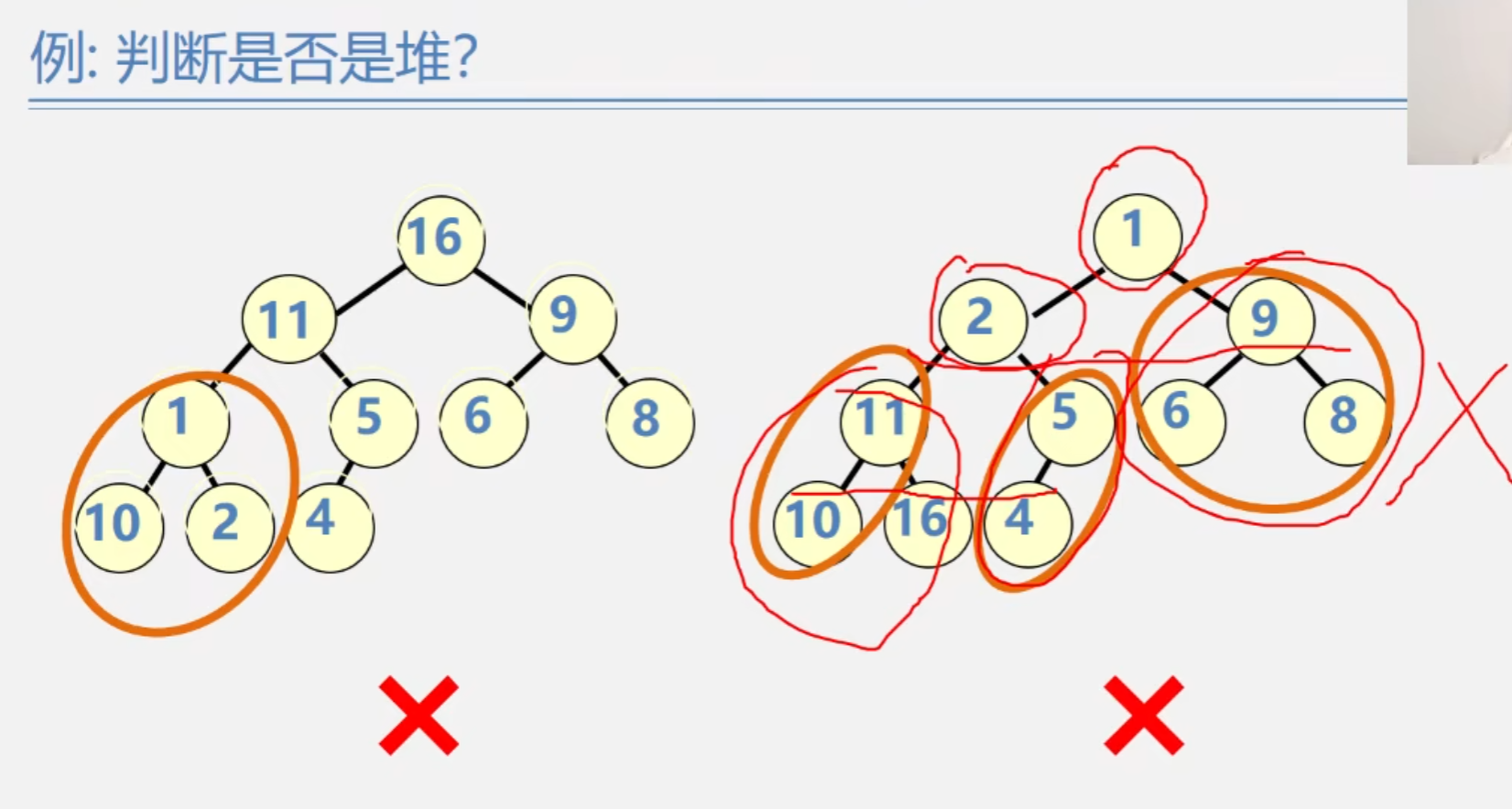
第一个不是堆

第二个也不是堆

如何进行堆排序?

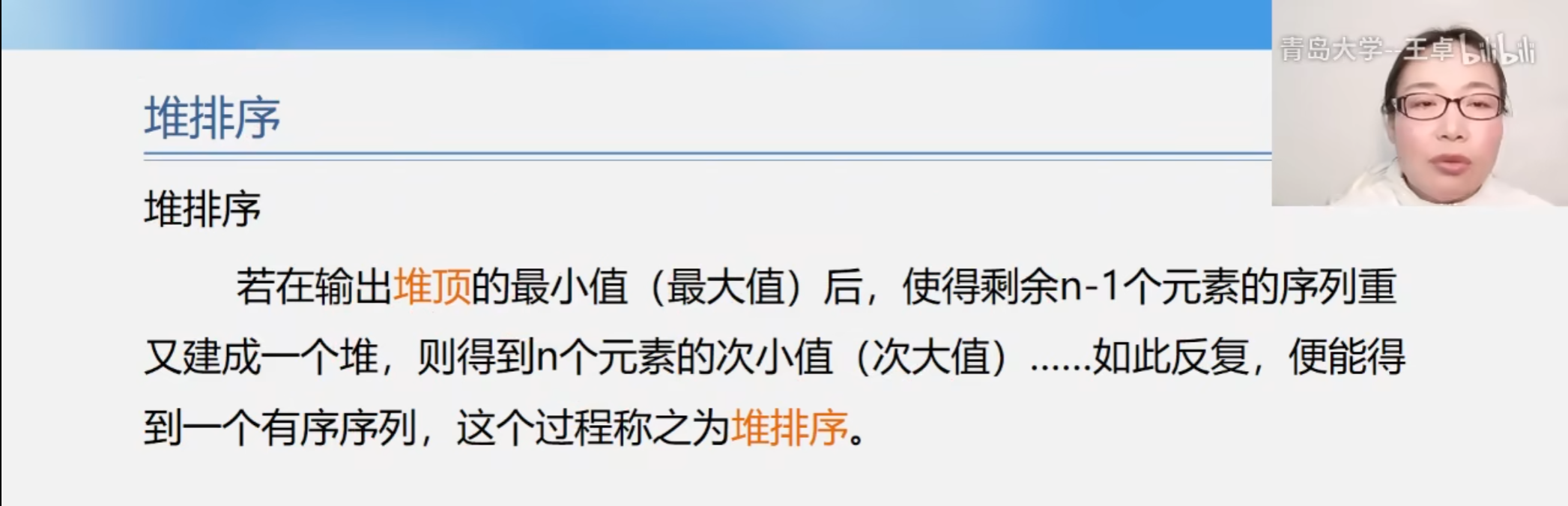
实现堆排序需要解决的两个问题.

堆调整

小根堆调整

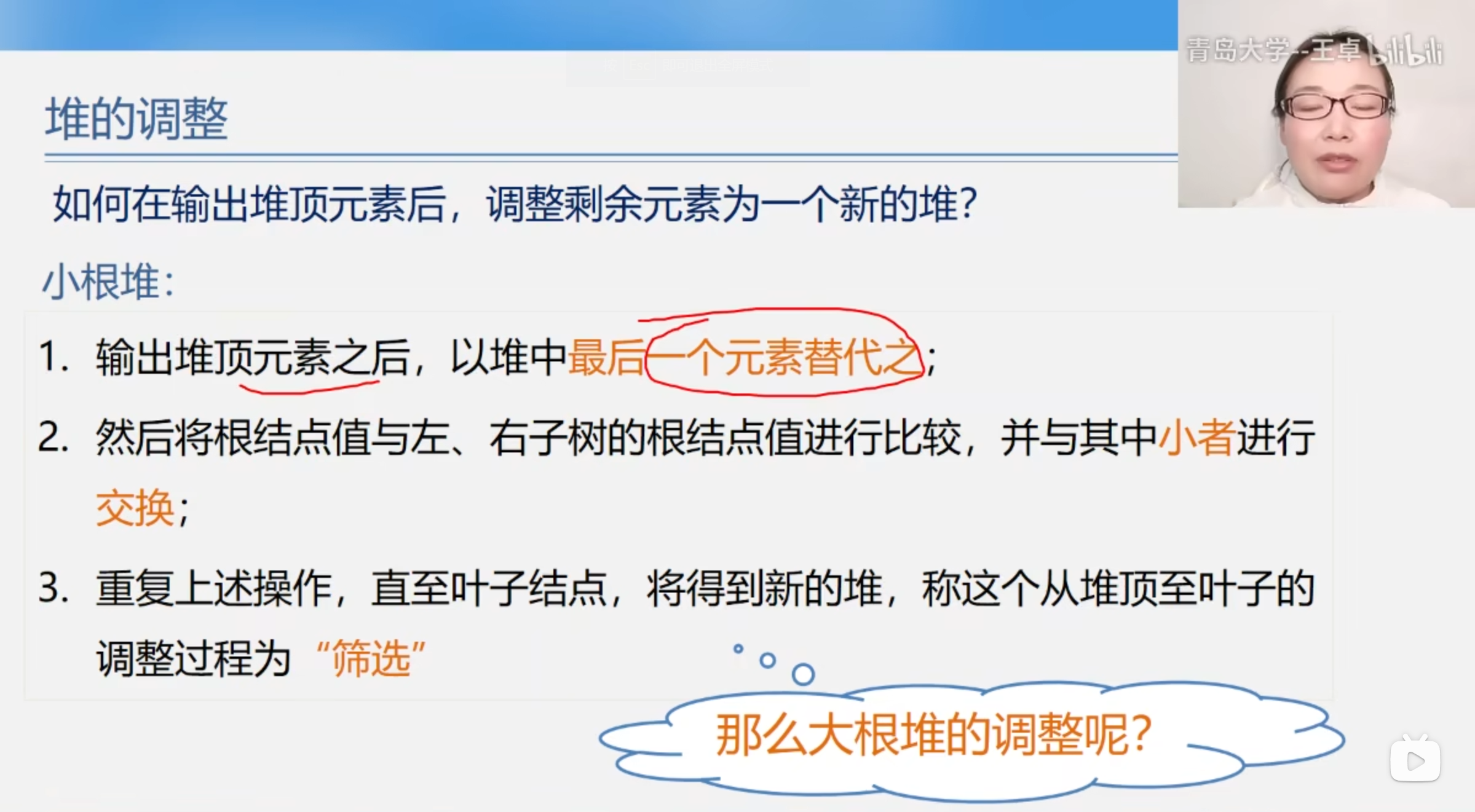
堆的调整例题

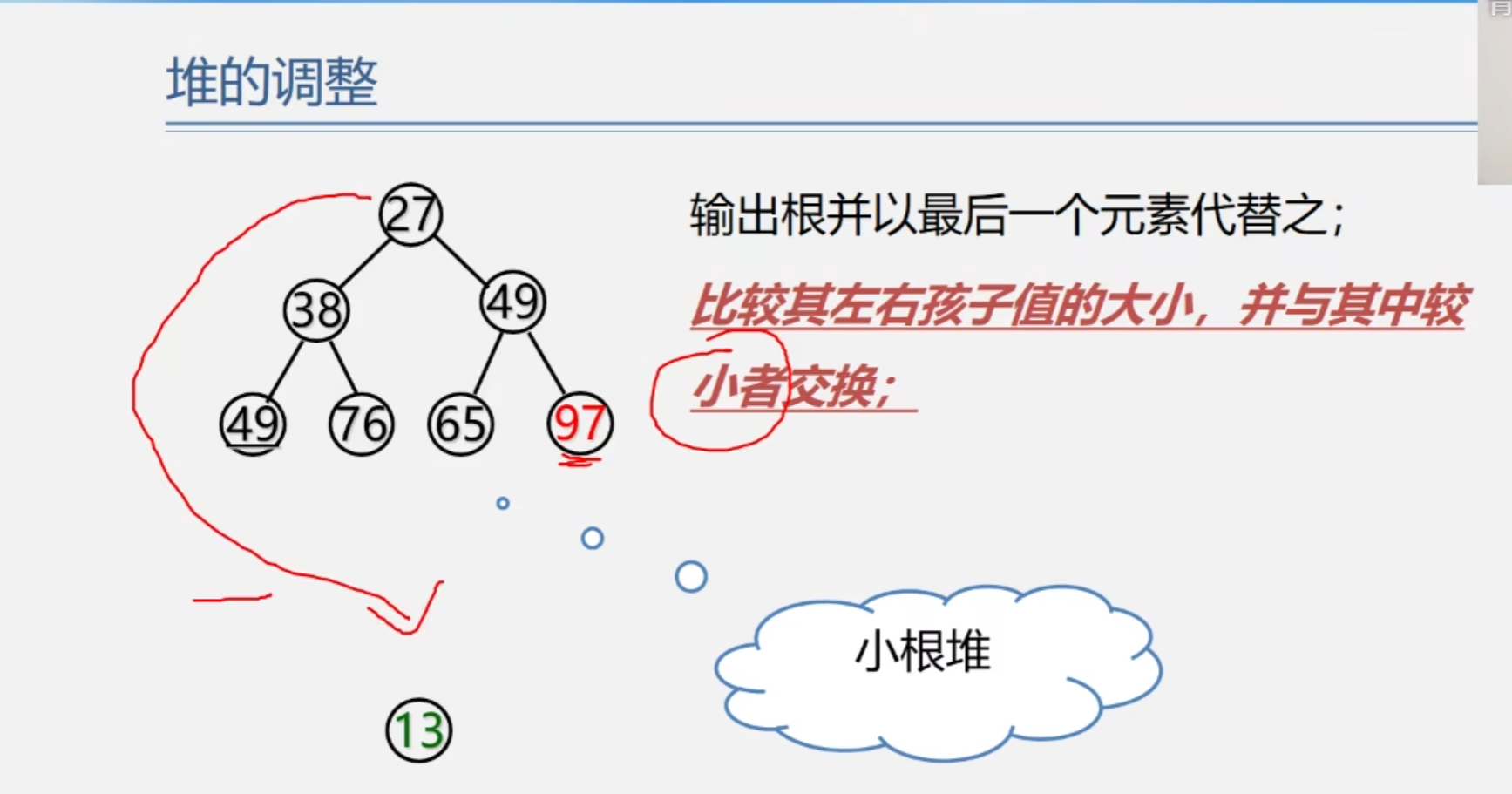
堆调整的算法

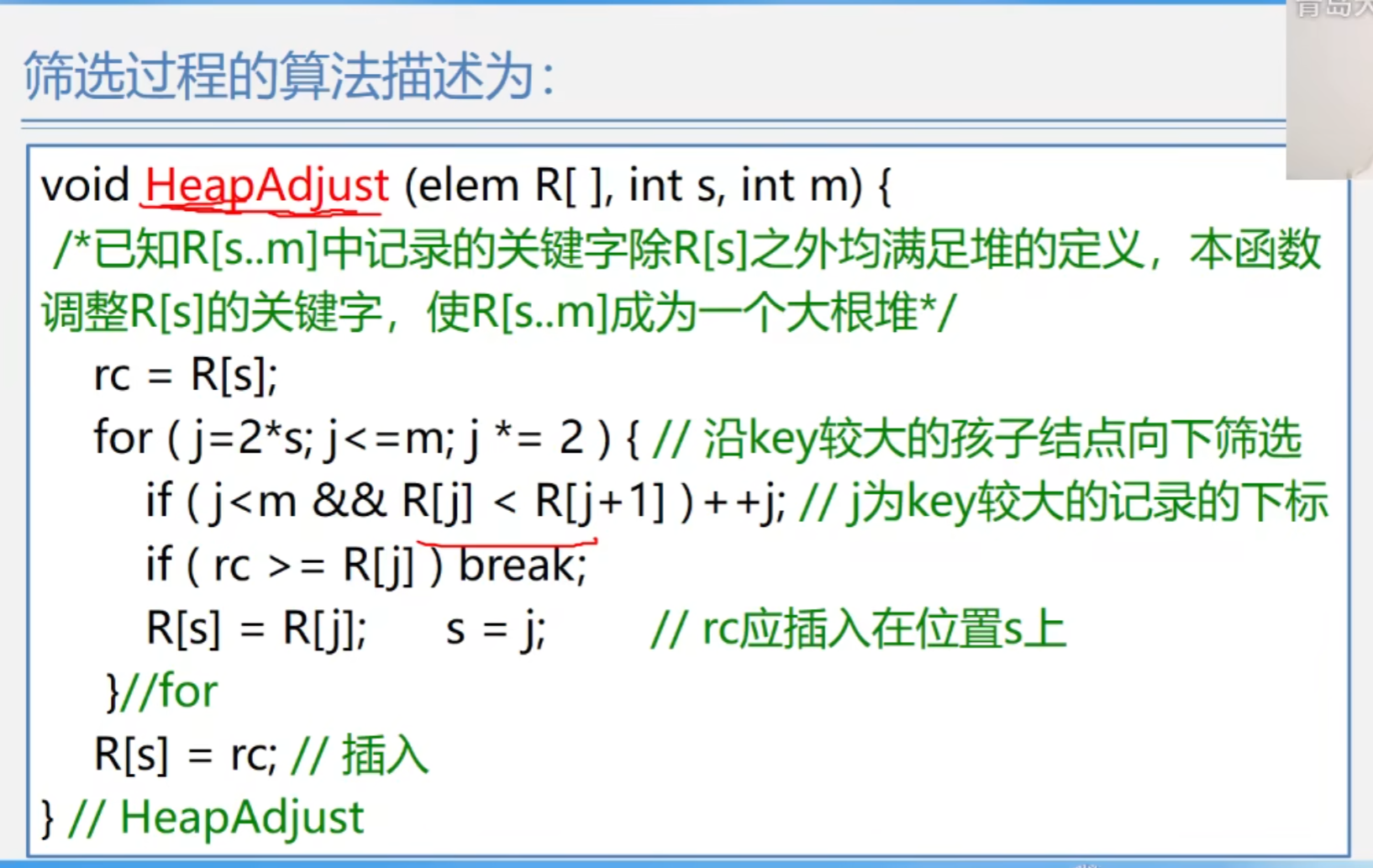
堆的调整过程

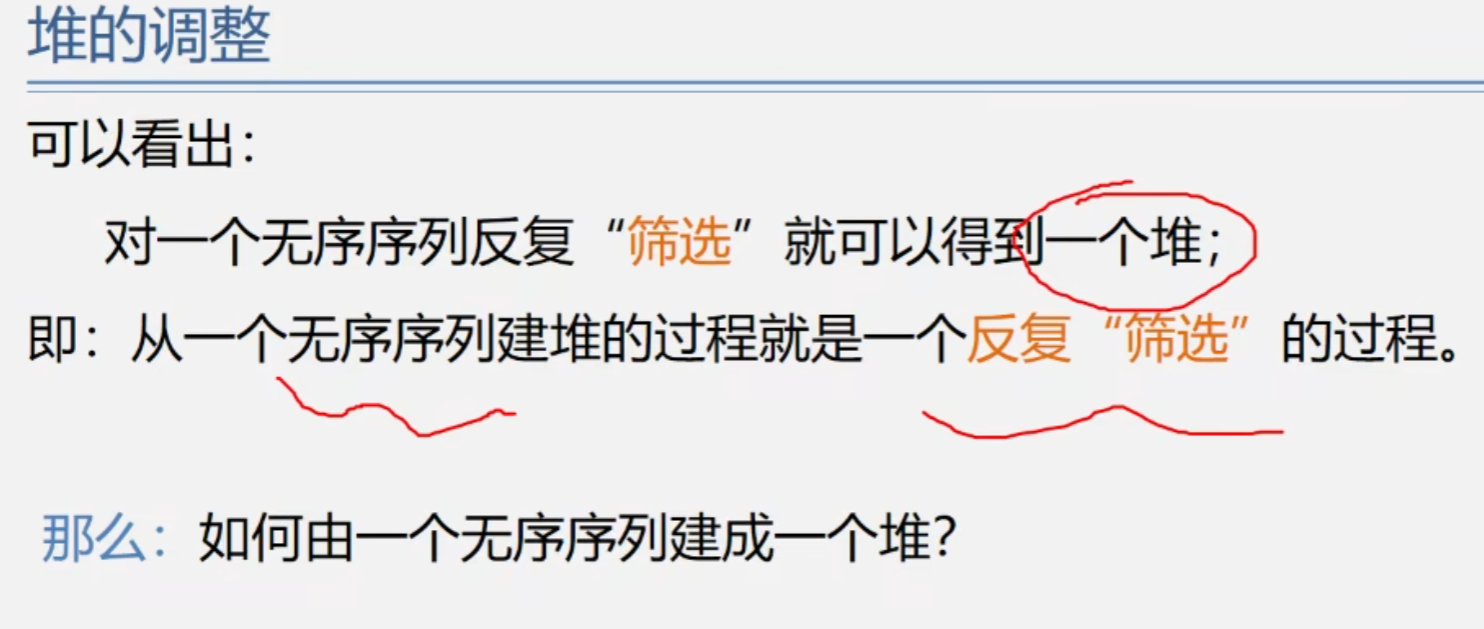
建立堆

将n/2,n/2-1,.....1的结点为根的子树均调整为堆即可.

堆实际上是一个线性表

下面是一个建立小根堆的过程.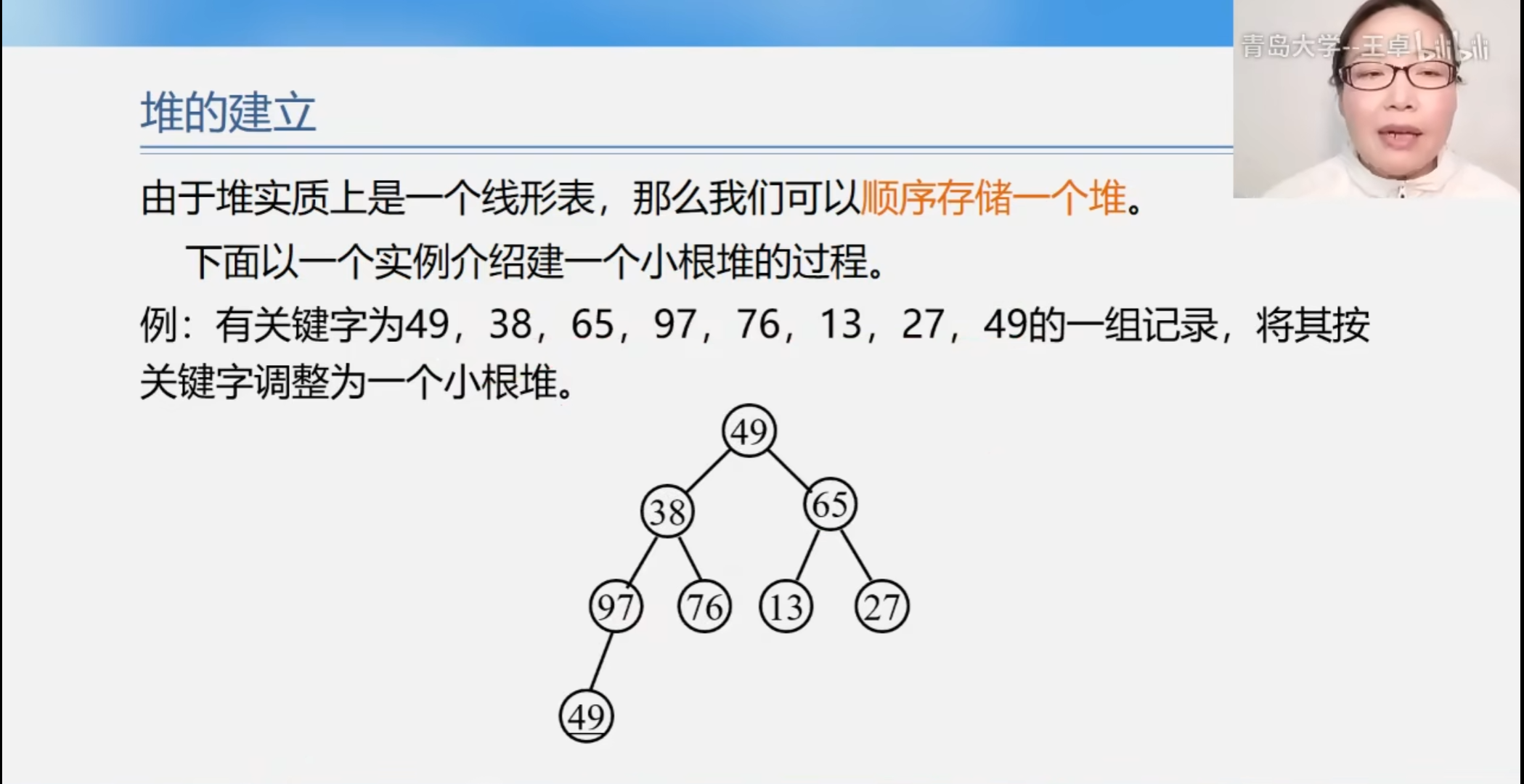

从最后一个非叶子结点开始,以此向前调整

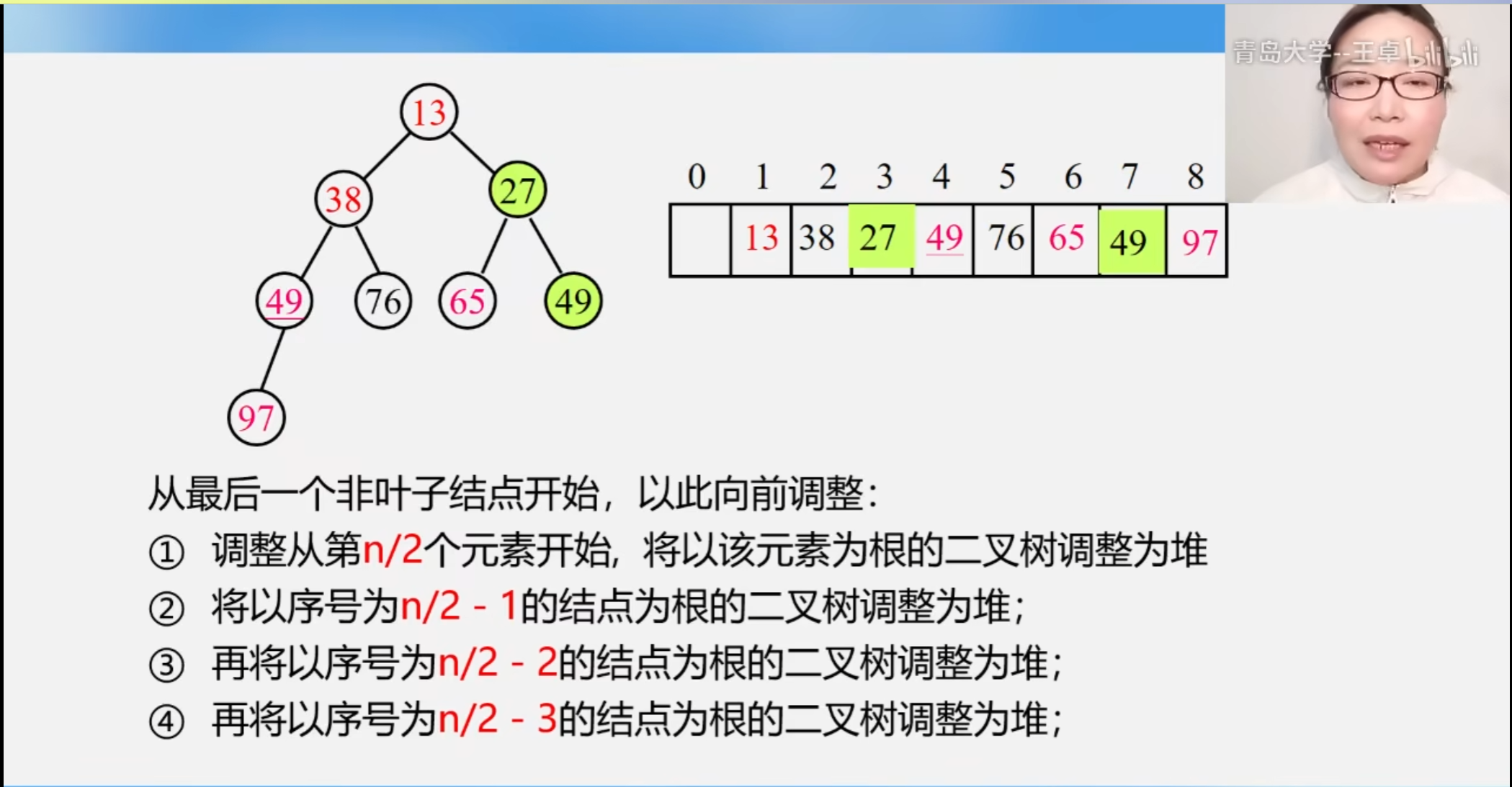
建立堆的算法实现

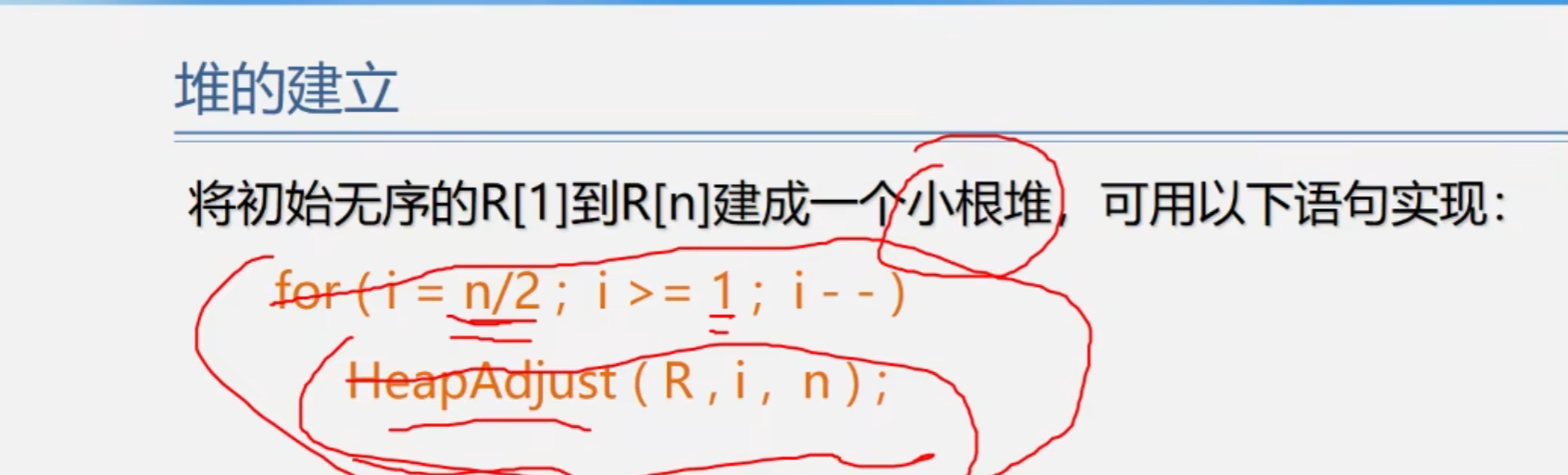
堆排序的算法分析

堆排序使用完全二叉树中父节点与孩子结点之间的内在关系来排序的

堆排序的算法实现

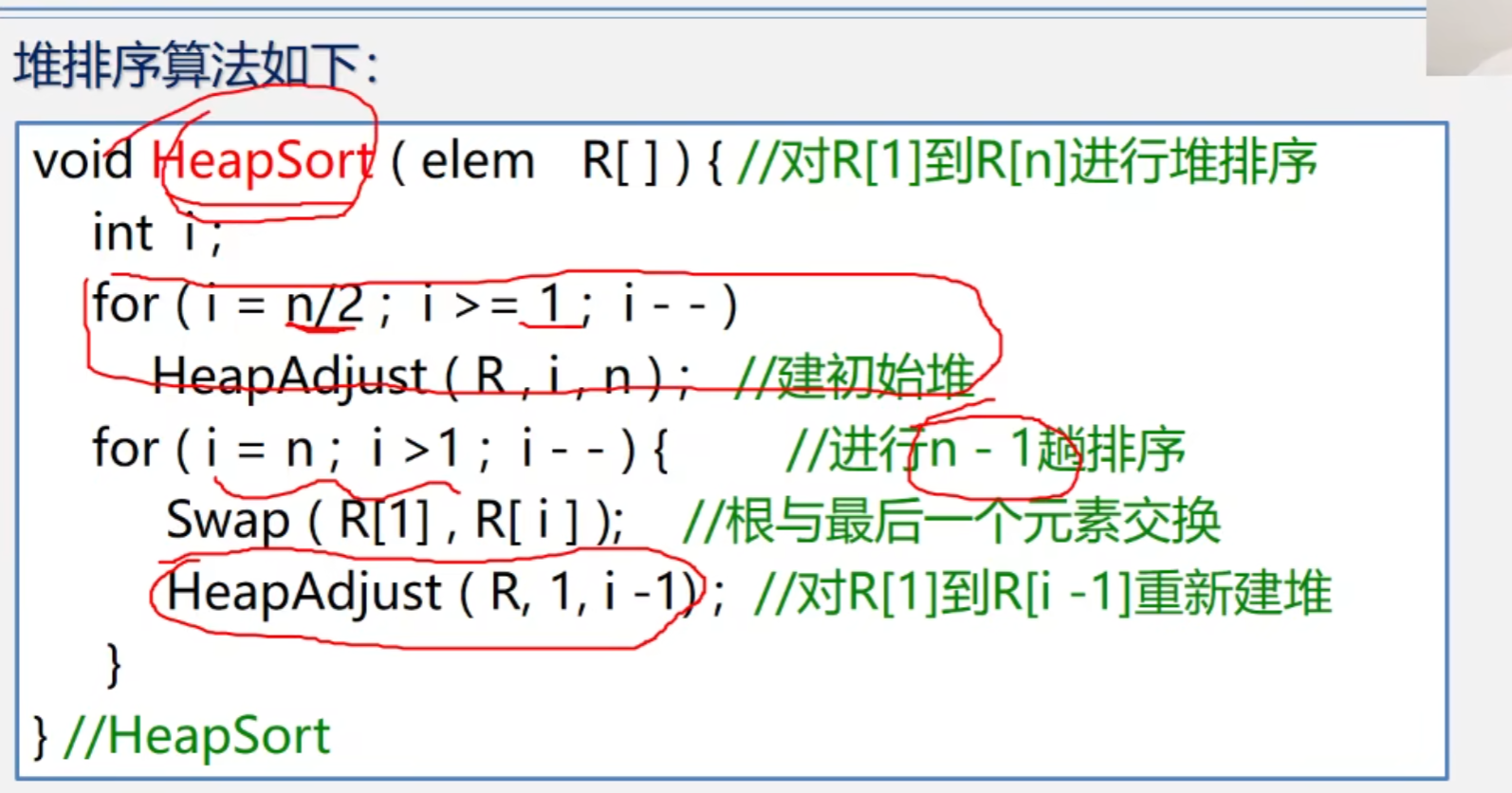
堆排序的代码实现

#include <bits/stdc++.h>
using namespace std;
void HeapAdjust(int arr[], int i, int n) {
	int largest = i; //初始化为i
	int lson = i * 2 + 1;
	int rson = i * 2 + 2; //左孩子和右孩子的下标
	if (lson < n && arr[largest] < arr[lson]) {
		largest = lson;
	}
	if (rson < n && arr[largest] < arr[rson]) {
		largest = rson;
	}
	//largest是最后保存的是需要交换的下标
	if (largest != i) { //说明需要调整堆
		swap(arr[largest], arr[i]); //交换这两个元素
		HeapAdjust(arr, largest, n); //递归的向下调整堆
	}
}
int main () {
	int arr[] = {8, 3, 1, 4, 5, 6, 3, 4, 2, 100, 140, 50, 60};
	int n = sizeof(arr) / (sizeof(int));
//	cout << n << '\n';
//	for (int i = 0; i < n; i++) {
//		cout << arr[i] << ' ';
//	}
//	cout << '\n';
	for (int i = n / 2 - 1; i >= 0; i--) { //建堆
		HeapAdjust(arr, i, n);
	}
	//堆排序
	for (int i = n - 1; i > 0; i--) {
		swap(arr[0], arr[i]);
		HeapAdjust(arr, 0, i);
	}
	for (int i = 0; i < n; i++) {
		cout << arr[i] << ' ';
	}
	cout << '\n';
	return 0;
}

堆优化需要的时间不超过O(logn)

n-1次循环所需要的时间不超过O(nlogn)

堆排序的时间复杂度总为O(nlogn)

堆排序不需要额外的空间,空间复杂度为O(1)