图的存储--邻接表
图的存储--邻接表
邻接表表示法
顶点:
按编号顺序将顶点数据储存在一维数组中;
关联同一顶点的边:
用线性链表储存.
头节点分为数据域和指针域.
表节点:
邻接点域:存放与vi邻接的顶点在表头数组中的位置.
链域:指向下一条边或弧.
还可以增加带权值的数据域info
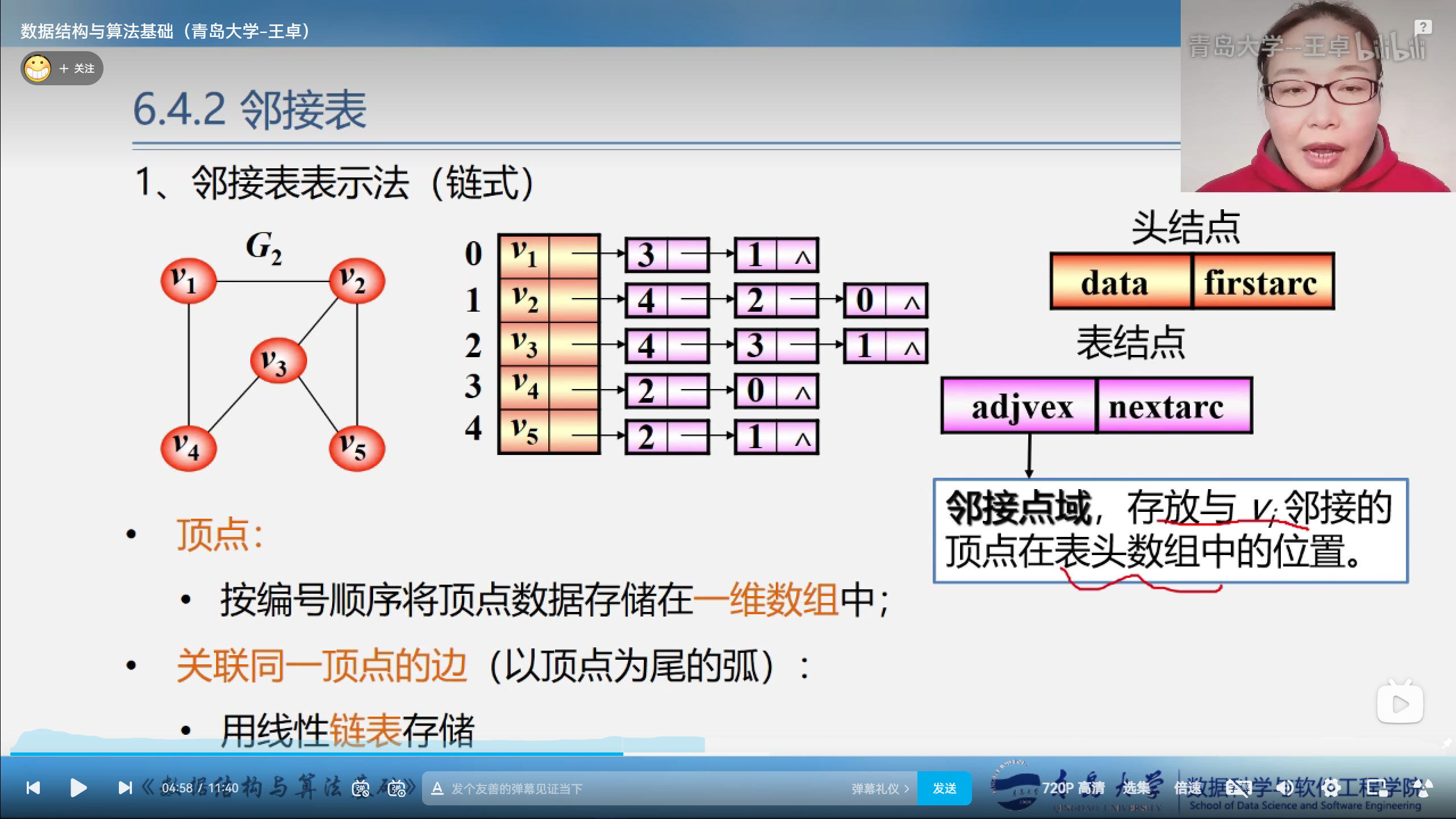
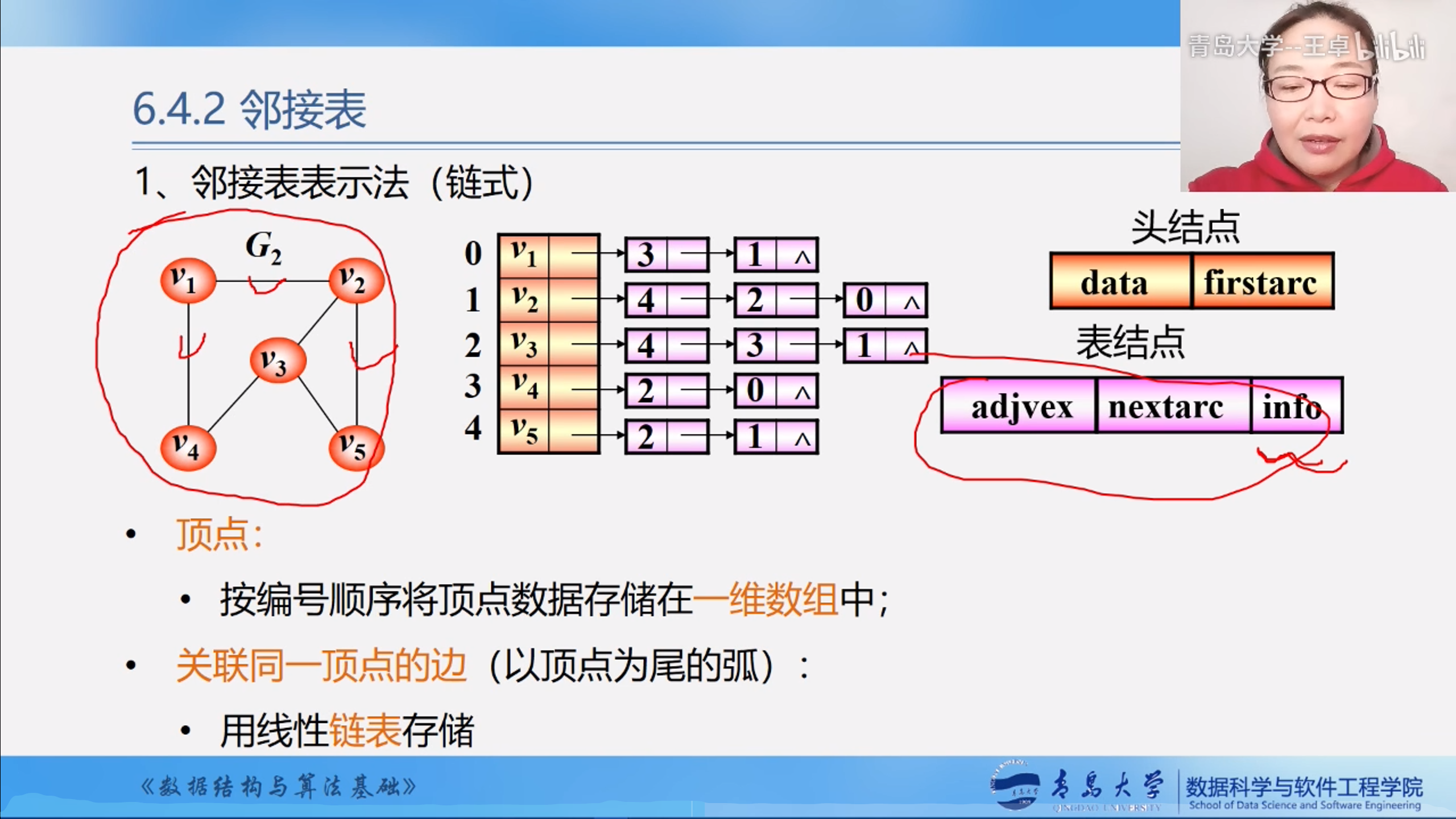
无向图的邻接表
- 邻接表不唯一
- 若无向图中有n个顶点,e条边,则其邻接表需n个头节点和2e个表节点.适宜存储稀疏图.
- 无向图中顶点vi的度为地i个单链表中的结点个数
有向图的邻接表
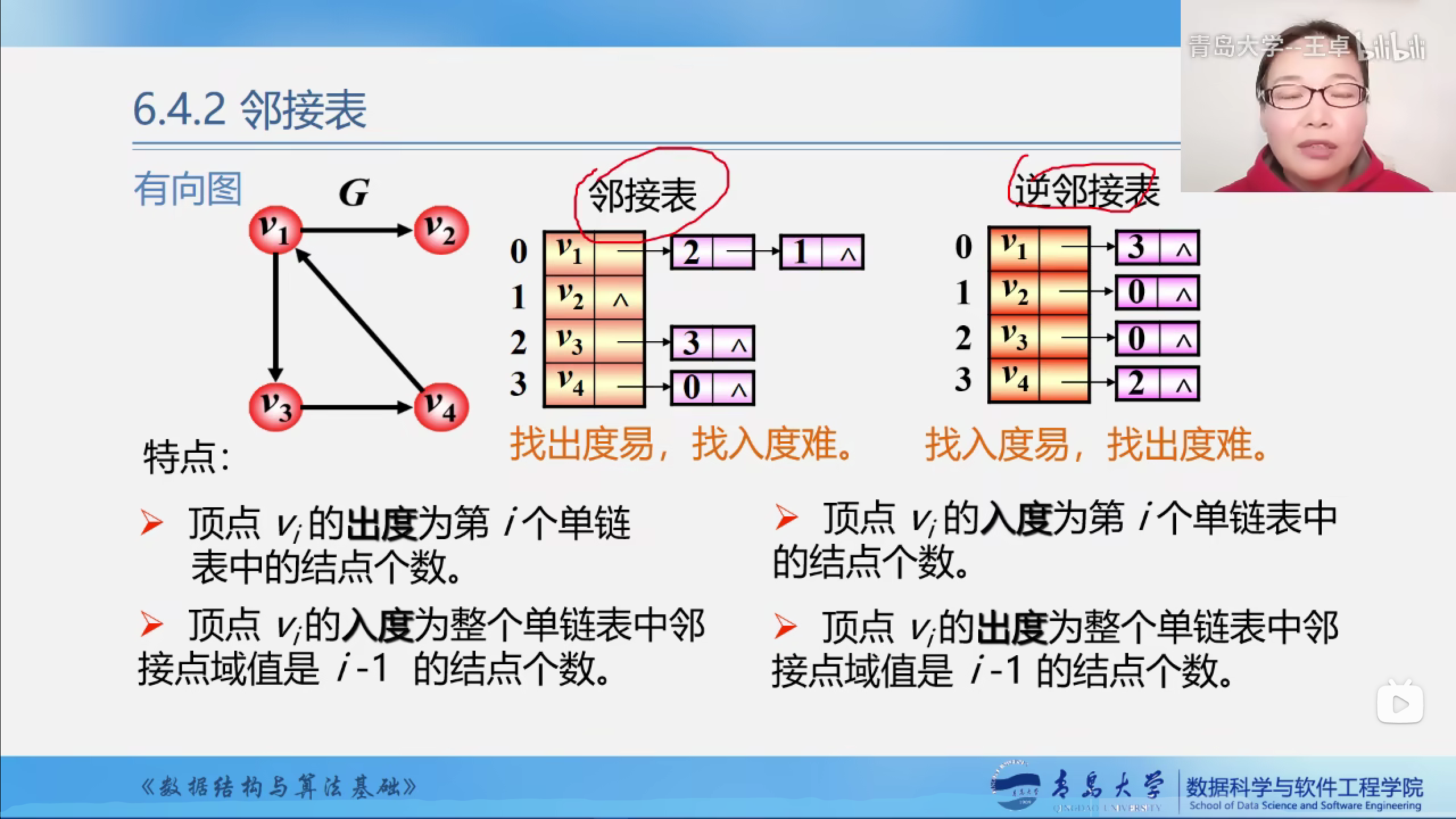
邻接表:
找出度容易,找入度难.
顶点vi的出度为第i个单链表的节点个数.
顶点vi的入度为整个单链表中邻接点域值是i-1的节点个数.
逆邻接表:
找入度易,找出度难.
顶点vi的入度为第i个单链表的节点个数.
顶点vi的出度为整个单链表中邻接点域值是i-1的节点个数.
练习
当邻接表的存储结构形成后,图便唯一确定了
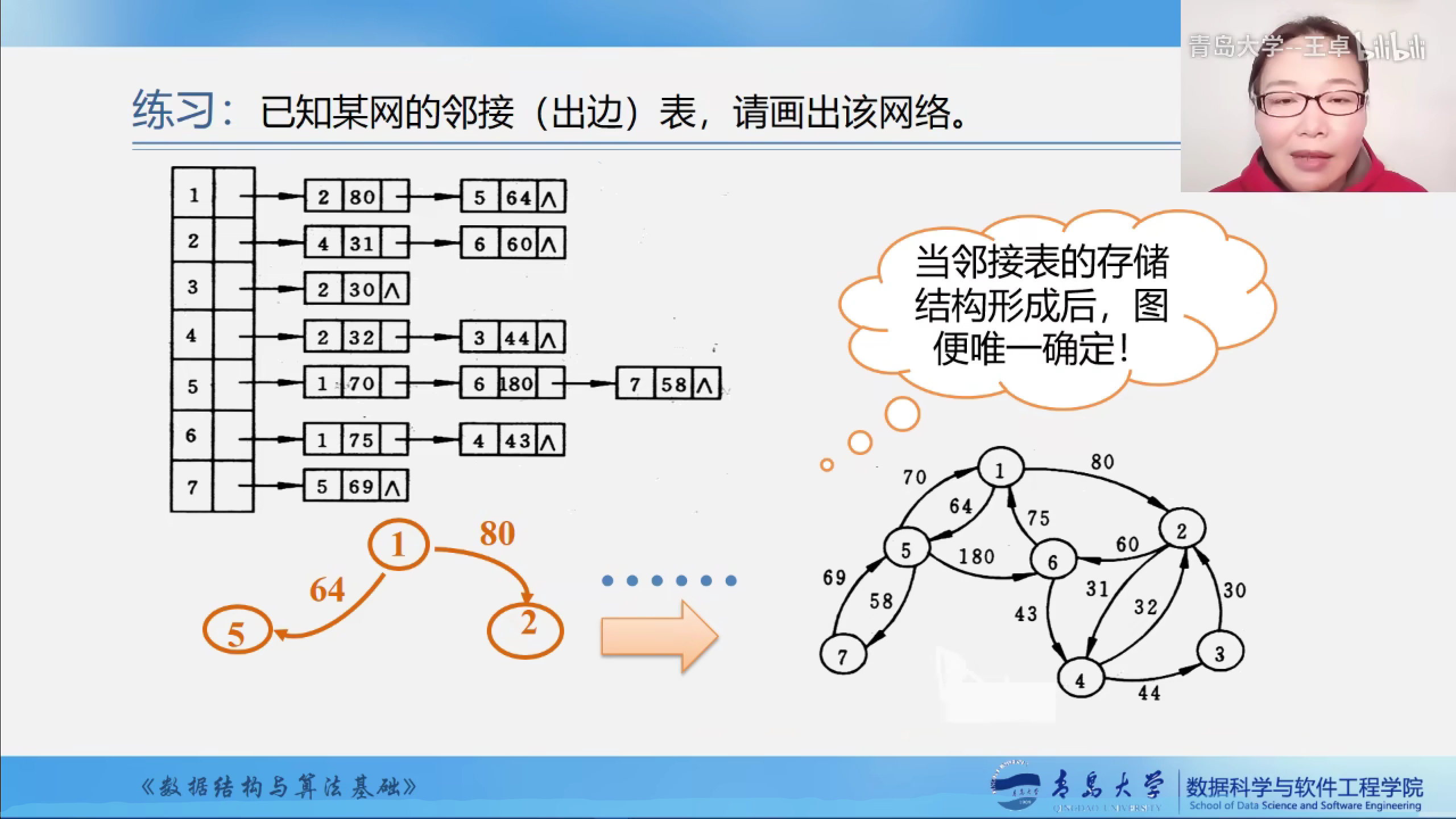
建立邻接表的算法
顶点的节点结构
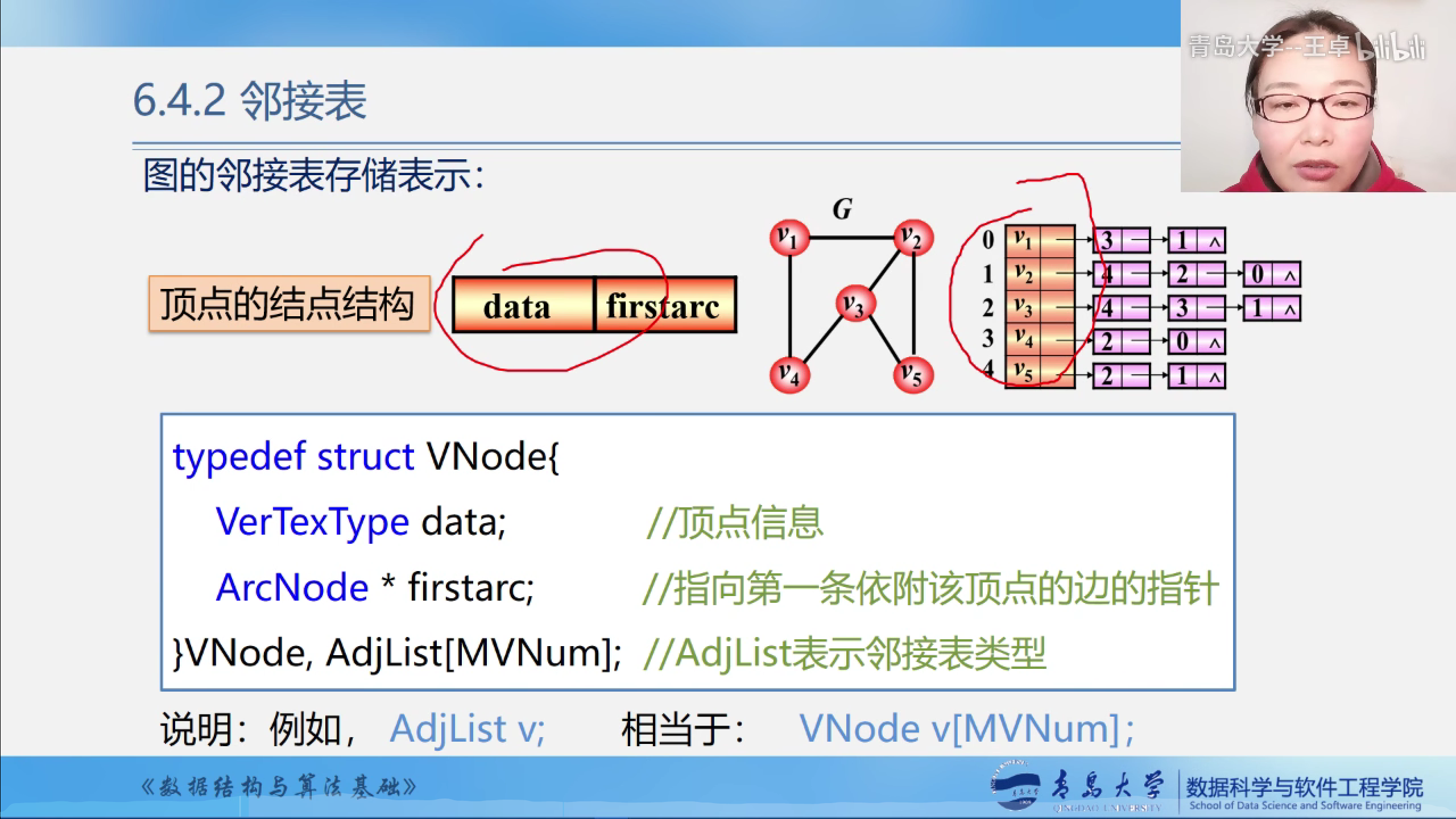
#include <bits/stdc++.h>
using namespace std;
typedef struct VNode {
int data;//顶点信息
int *firstarc;//指向后面每一条边的指针
} VNode, AdjList[10];
int main () {
AdjList v;
return 0;
}
弧(边)的节点结构
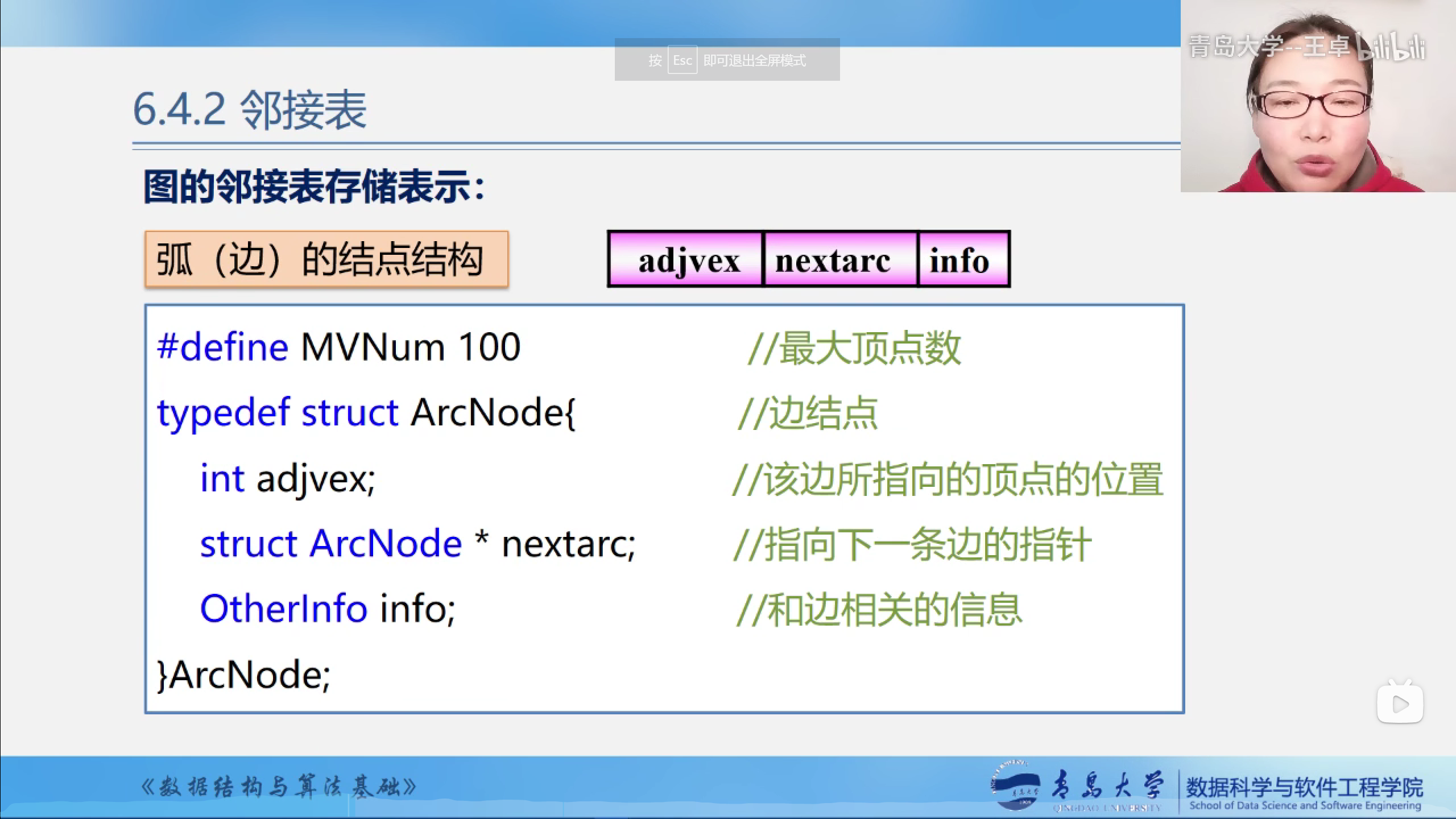
typedef struct ArcNode { //定义边节点的类型
int adjvex;//储存下一个点的下标
struct ArcNode* nextarc;//指向下一个顶点
int info;//储存权值
} ArcNode;
图的结构定义
typedef struct{
AdjList vertices;
int vexnum,arcnum;
//图的当前顶点数和弧数
}ALGraph;//图的类型定义
邻接表操作说明
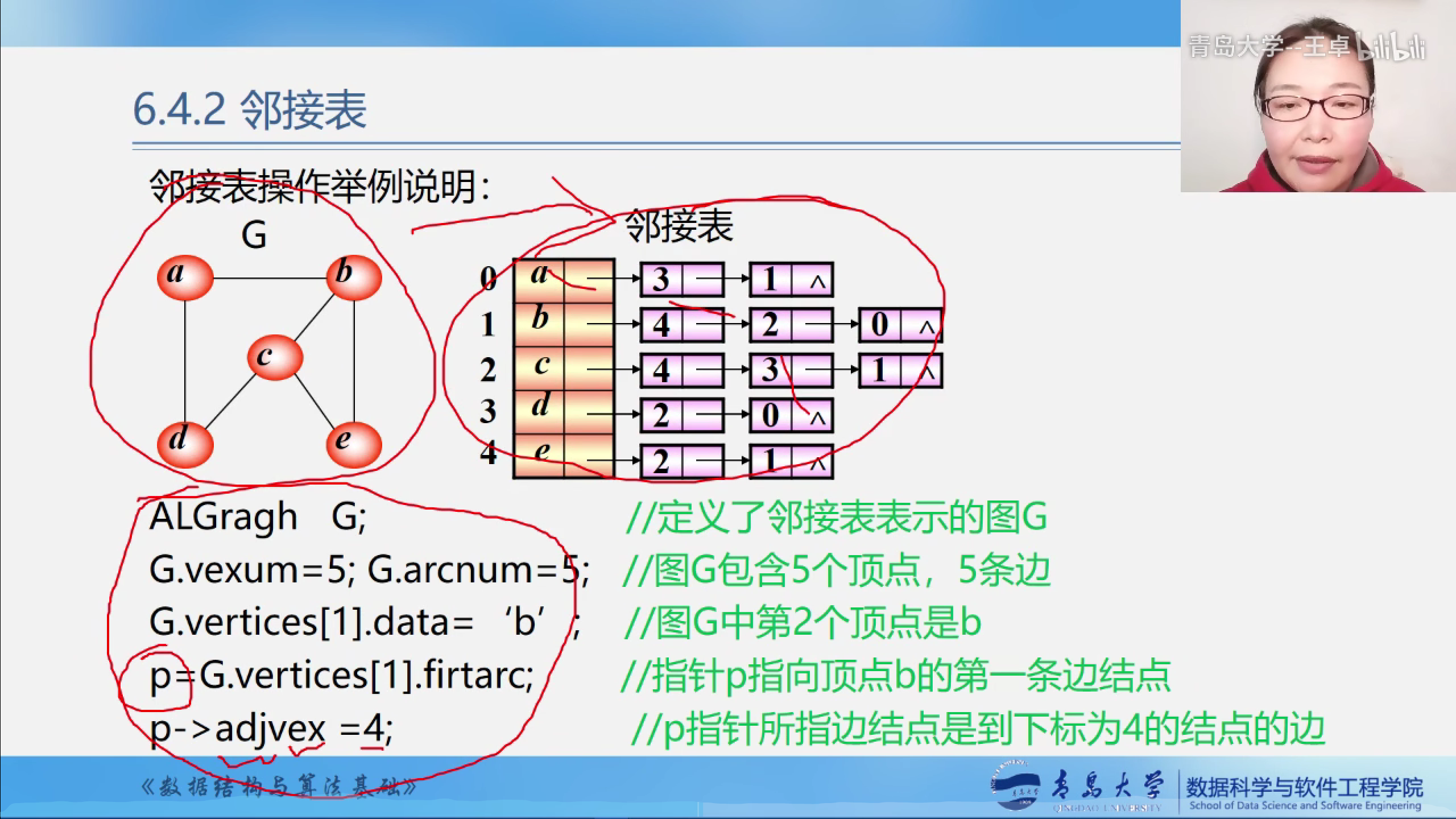
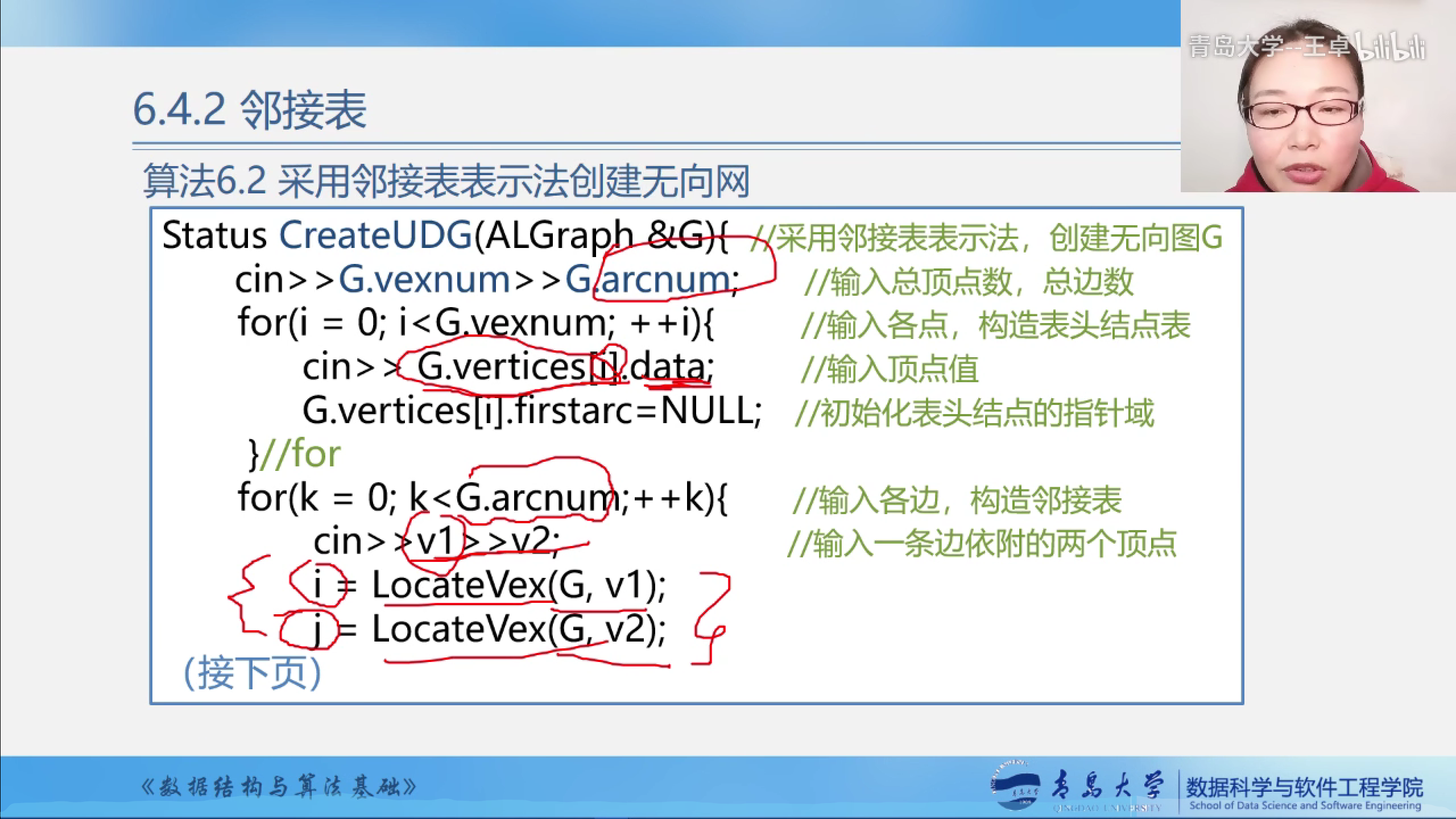
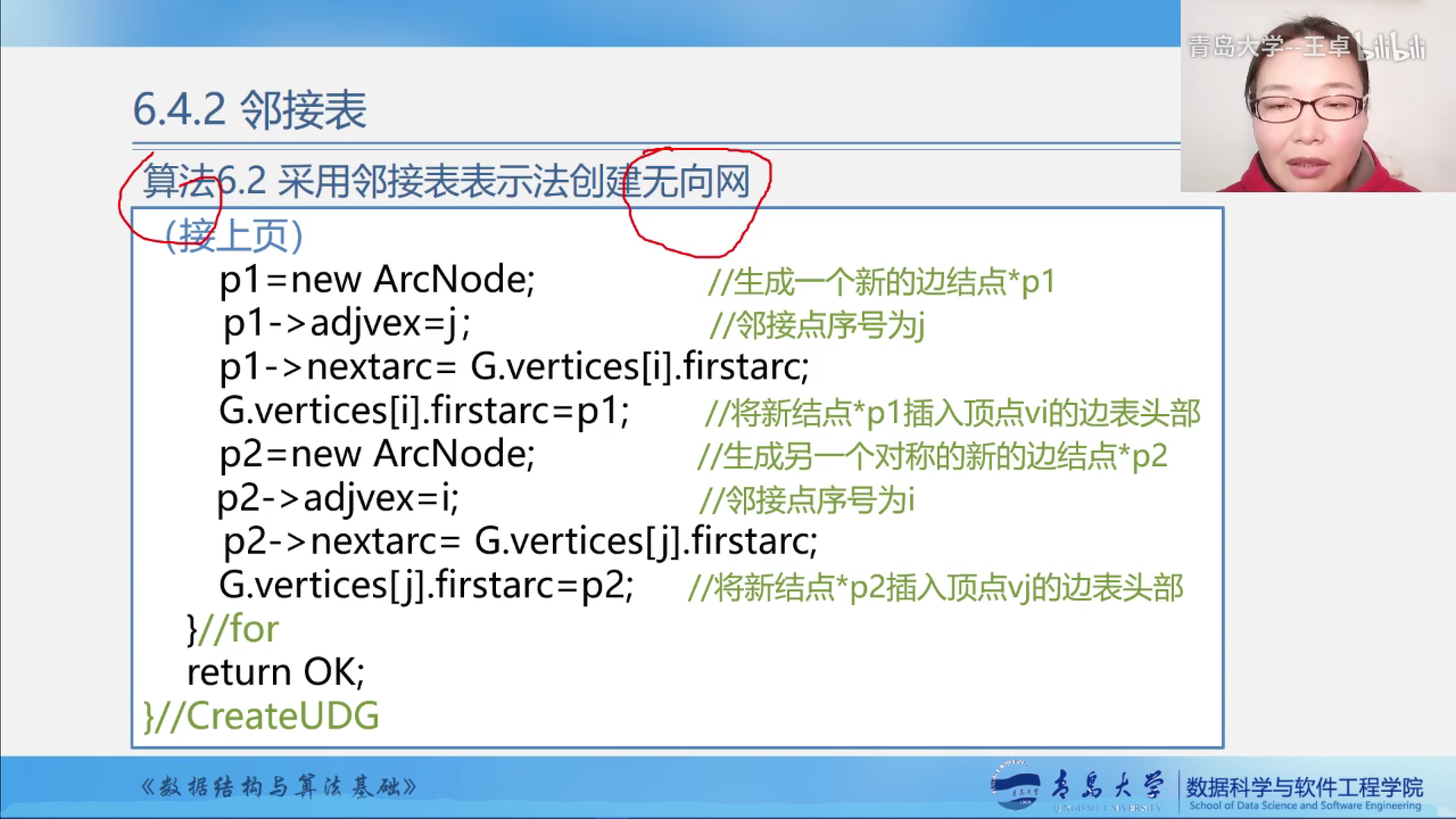
采用邻接表创建无向网.
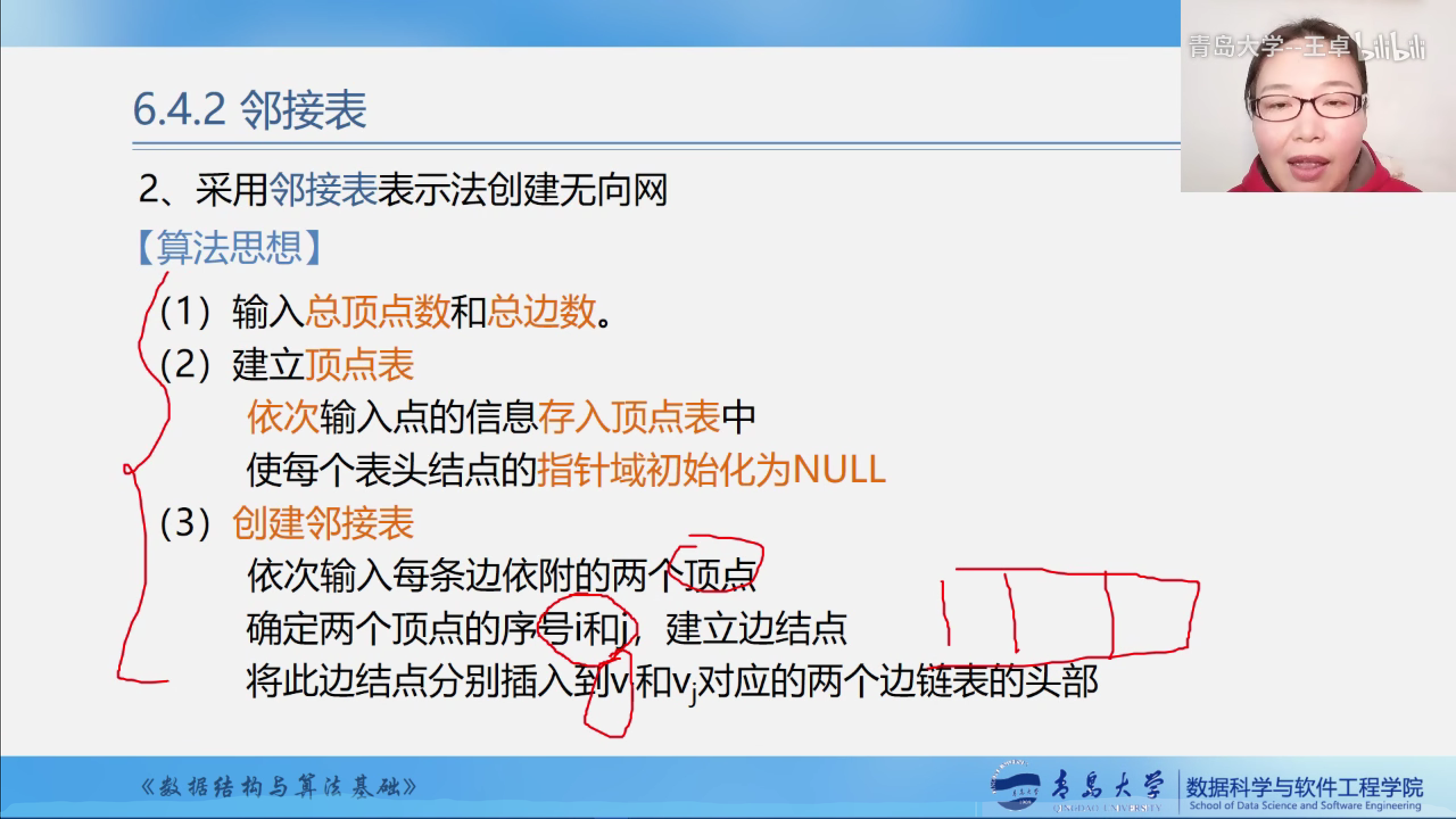
算法实现--采用邻接表创建无向网.
邻接表和矩阵的优缺点
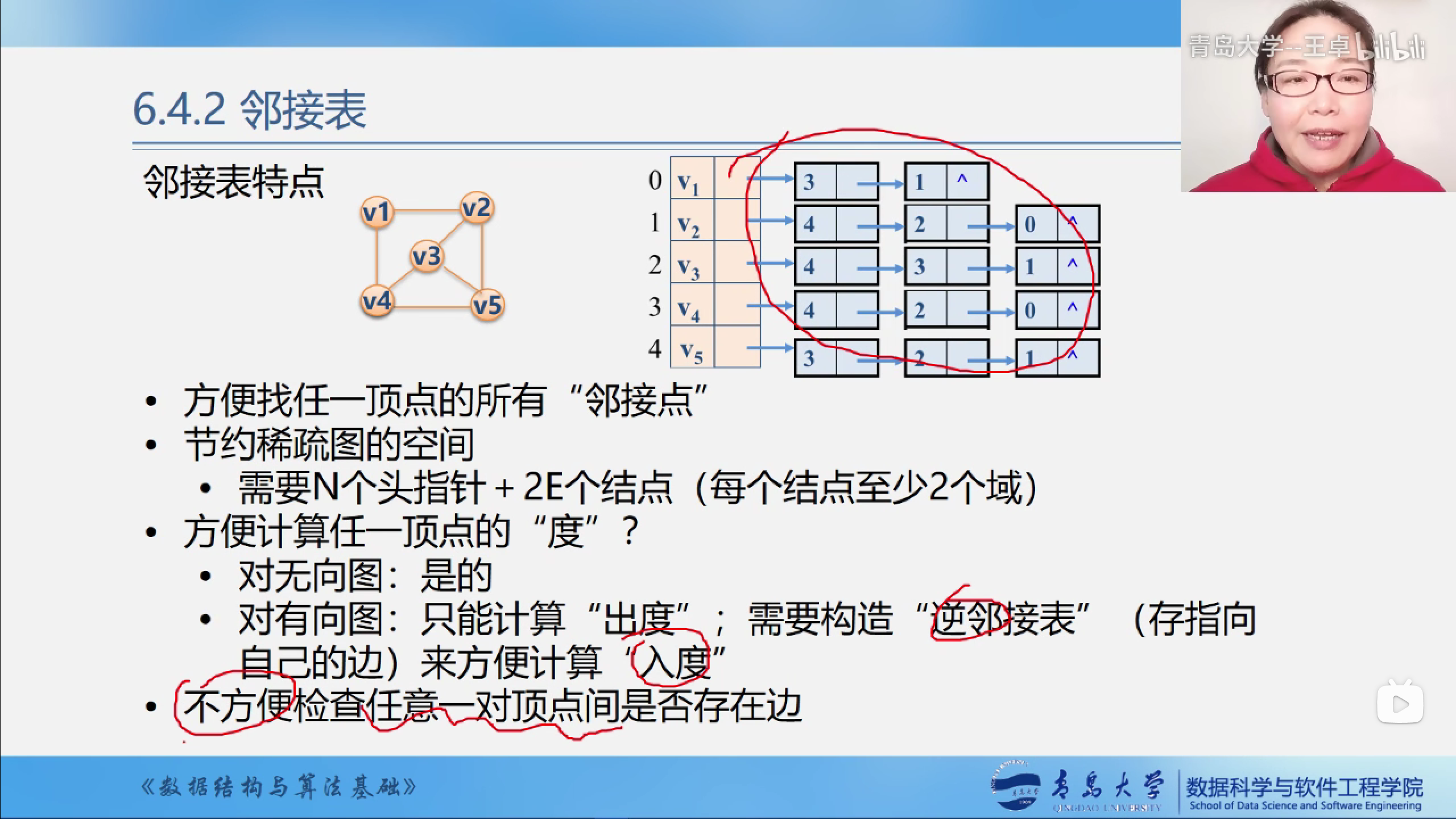
邻接表的特点
方便找任一顶点的所有"邻接点".
节约稀疏图的空间.
方便计算每一个顶点的度?
无向图容易计算
有向图不容易计算
不方便检查任意一对顶点间是否存在边.
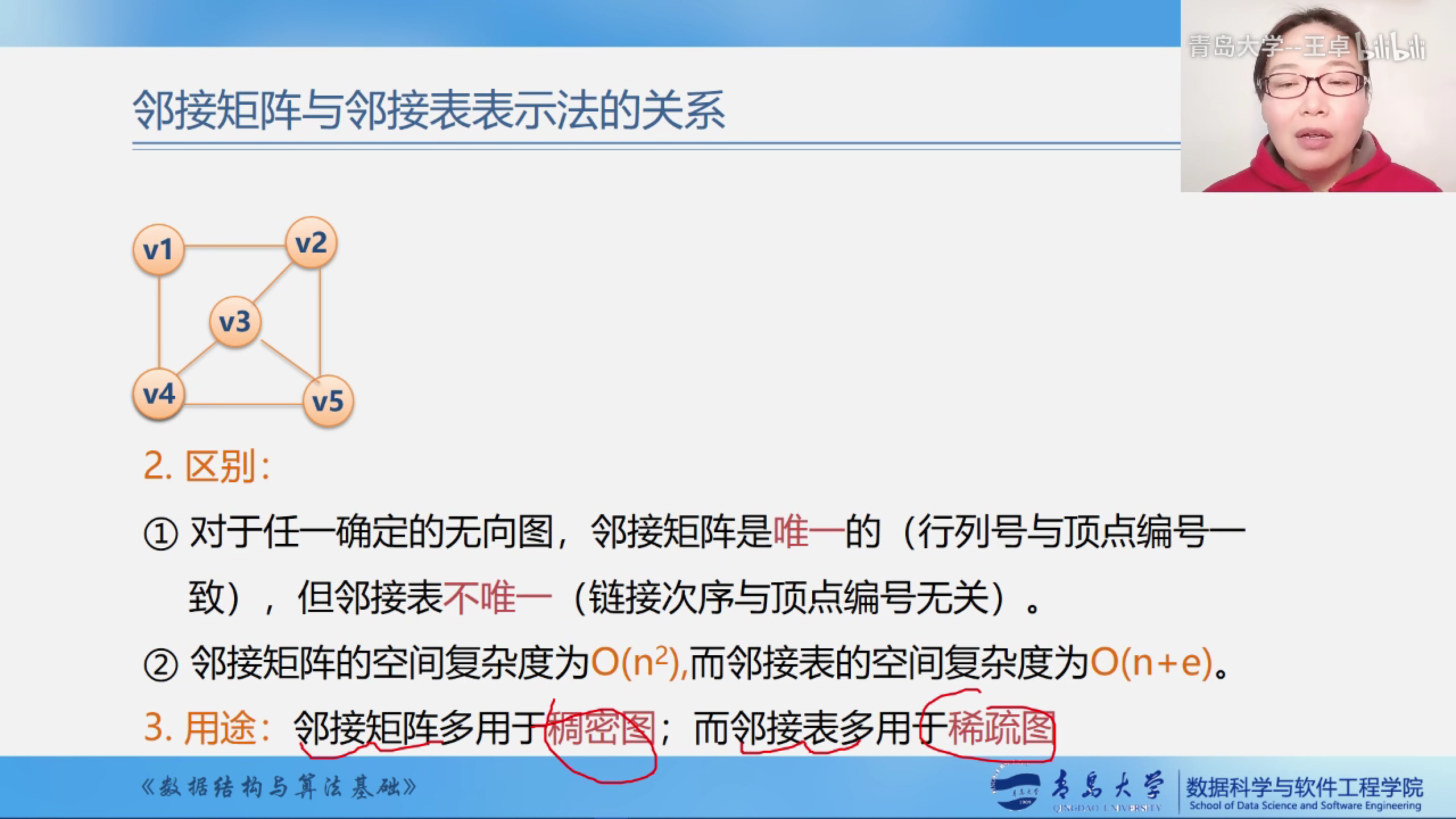
邻接矩阵和邻接表之间的关系
- 联系:邻接表中每个链表对应于邻接矩阵中的一行,链表中节点个数等于一行中非零元素的个数.
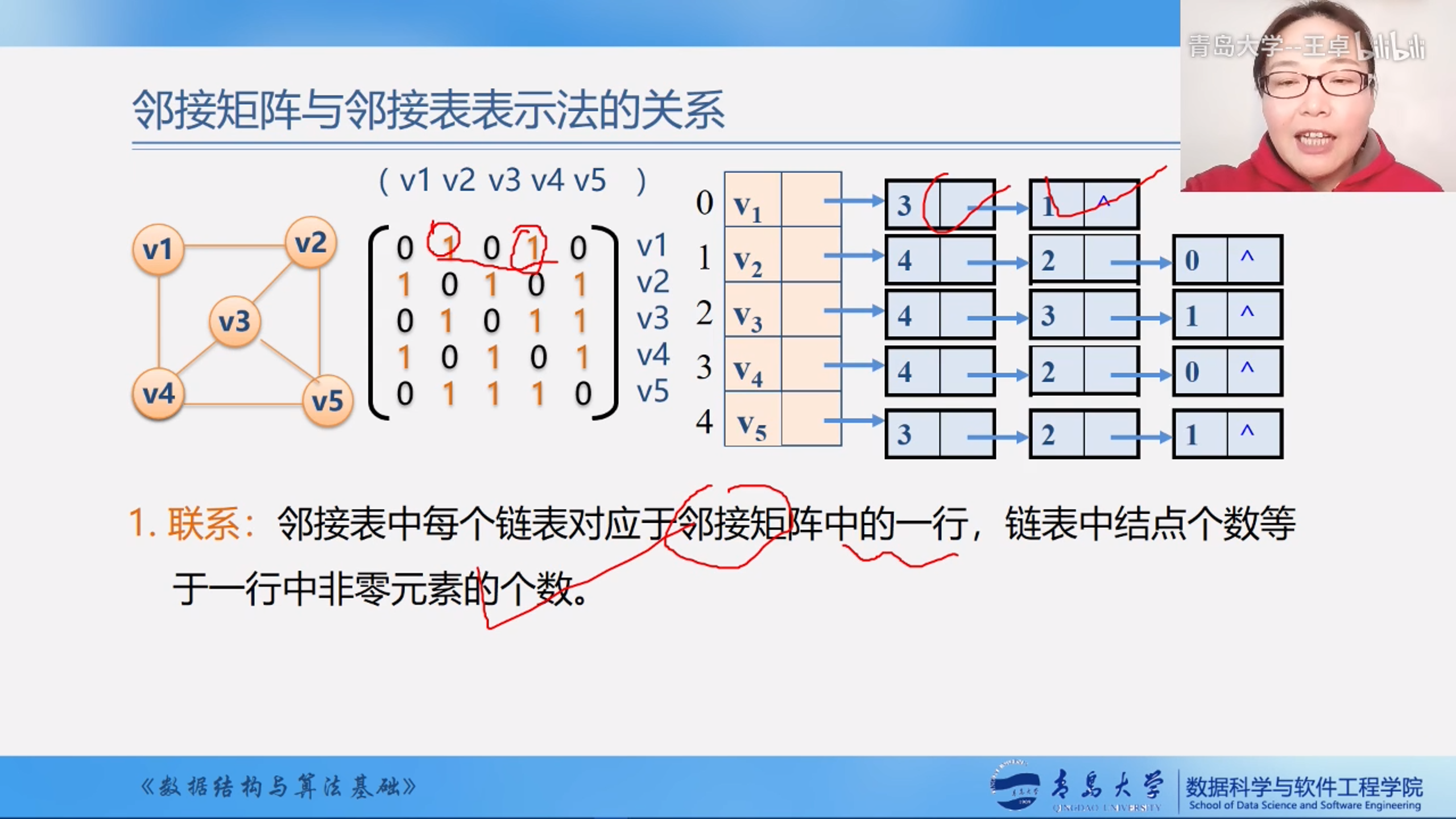
- 区别:对于任一确定的无向图,邻接矩阵是唯一的(行列号与顶点编号一致),但邻接表不唯一(链接次序与顶点的编号无关).
- 邻接表的空间复杂度为O(n^2),而邻接表的空间复杂度为O(n+e).
- 用途:邻接矩阵多用于稠密图,而邻接表多用于稀疏图.
