邻接矩阵表示法

邻接矩阵表示法

使用邻接矩阵创建无向图

需要一个顶点表和邻接矩阵

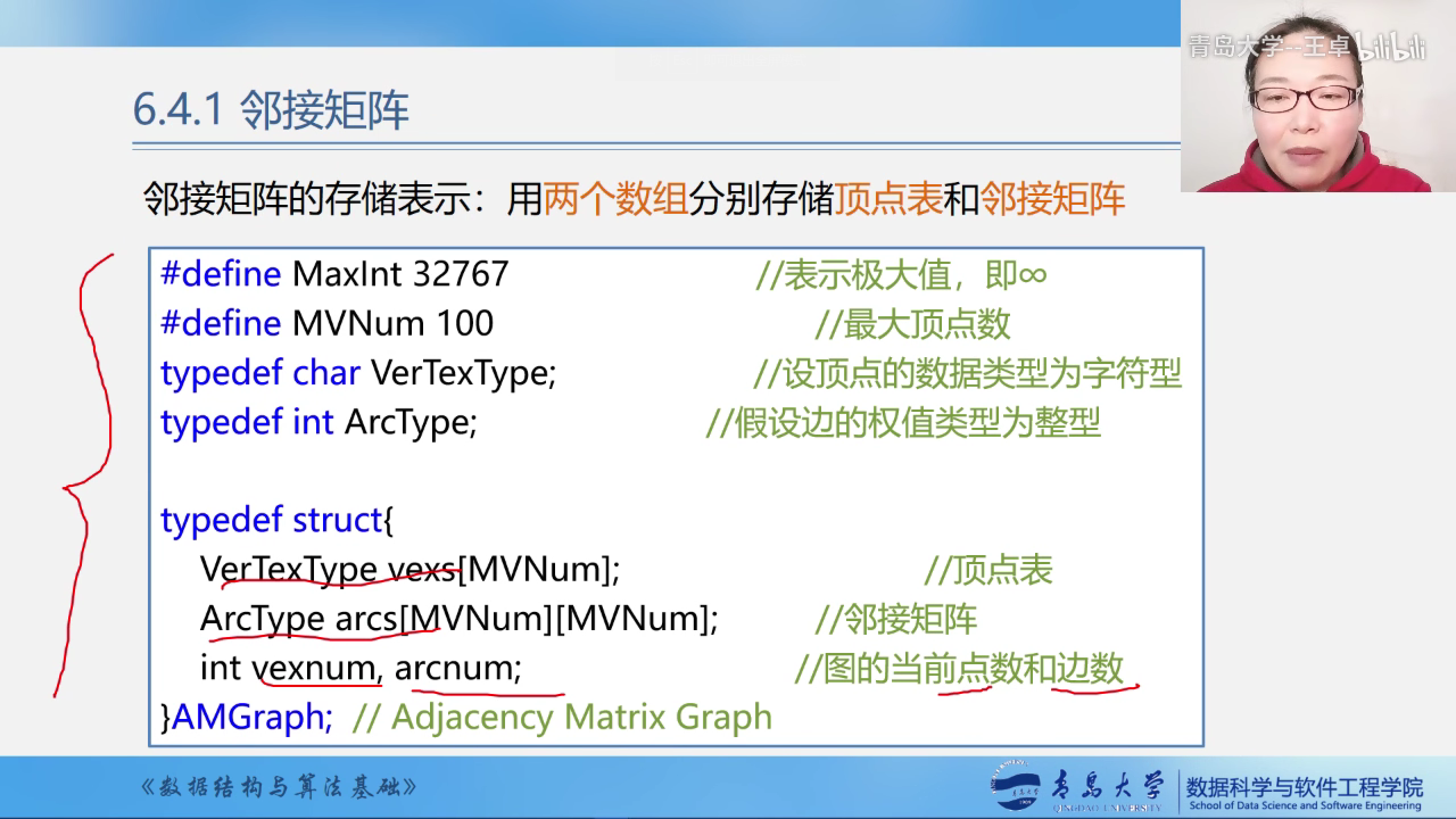
邻接矩阵的存储结构

采用邻接矩阵建立无向网

1. 输入总顶点数和总边数。
2. 输入点的信息存入顶点表中。
3. 初始化化为邻接矩阵，使每个权值初始化为极大值。
4. 构造邻接矩阵

算法实现

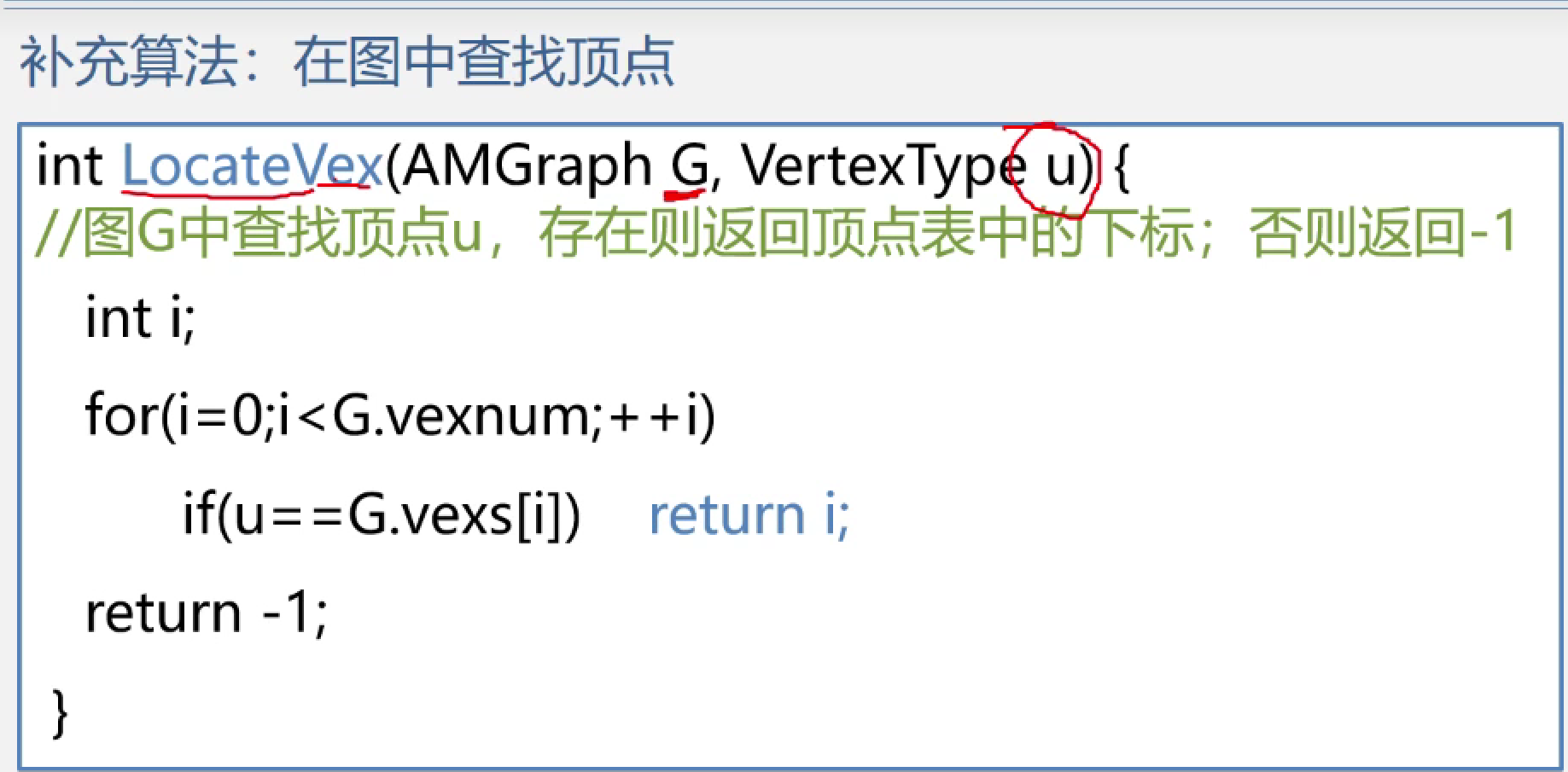
在图中查找顶点

代码实现

#include <bits/stdc++.h>
#define  MVnum 100
//定义最大值
using namespace std;
typedef pair<int, int> PII;
const int N = 100008;

typedef struct { //邻接矩阵的存储结构
	int vexs[MVnum];//定义一个顶点表
	int arcs[MVnum][MVnum];//定义一个邻接矩阵
	int vexnum, arcnum;

} AMGraph;
int Localevex(AMGraph G, int u) {
	for (int i = 0; i < G.vexnum; i++) {
		if (u == G.vexs[i]) {
			return i;//找到返回下标值,没有找到返回-1
		}
	}
	return -1;
}
/*
  该函数用来建立邻接矩阵
  参数为邻接矩阵的结构类型
 */
void Create(AMGraph& G) {
	cin >> G.vexnum >> G.arcnum; //读入顶点数和边数
	for (int i = 0; i < G.vexnum; i++) {
		cin >> G.vexs[i]; //读入顶点表的值
	}
	for (int i = 0; i < G.vexnum; i++) {
		for (int j = 0; j < G.vexnum; j++) {
			G.arcs[i][j] = 0x3f3f3f3f; //赋值为无穷大
		}
	}
	//构造邻接矩阵
	int v1, v2, w;
	for (int k = 0; k < G.arcnum; k++) {
		cin >> v1 >> v2 >> w;
		int i = Localevex(G, v1);
		int j = Localevex(G, v2); //找到符合下标位置
		G.arcs[i][j] = w; //无向图建立两条边
		G.arcs[j][i] = w; //仿佛权值


	}


}
int main () {
	AMGraph G;
	Create(G);

	return 0;
}

无向图的邻接矩阵存储

1. 初始化邻接矩阵,w均为0.
2. 构造邻接矩阵的时候,w为1.

有向图的邻接矩阵存储

邻接矩阵是非对称矩阵

只给G.arces(i)(j)赋值,

无需为G.arces(j)(i)赋值

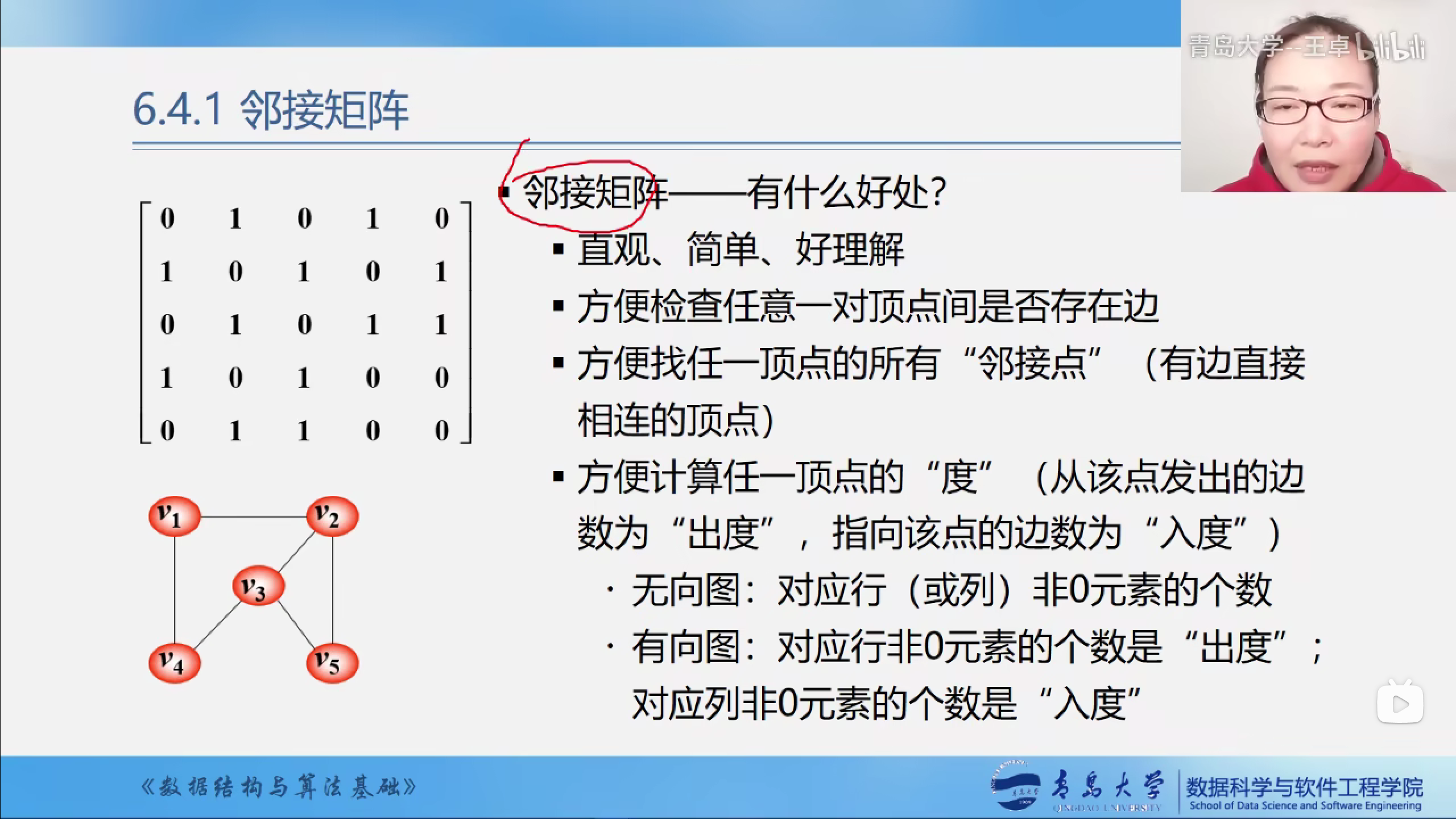
邻接矩阵的优缺点

优点

1. 直观,简单,好理解

2. 方便检查任意一对顶点间是否存在边

3. 方便计算任一顶点的所有邻接点.

4. 方便计算任一顶点的度.

缺点

1. 不便于增加和删除顶点
2. 浪费空间--稀疏图有大量无效元素.
3. 浪费时间--统计稀疏图一共有多少条边.