数据结构---图

数据结构---图的基本概念

图的定义和基本术语

V:顶点的有穷非空集合

E:边的有穷集合

无向图:每条边都是无方向.

有向图:每条边都是有方向的.

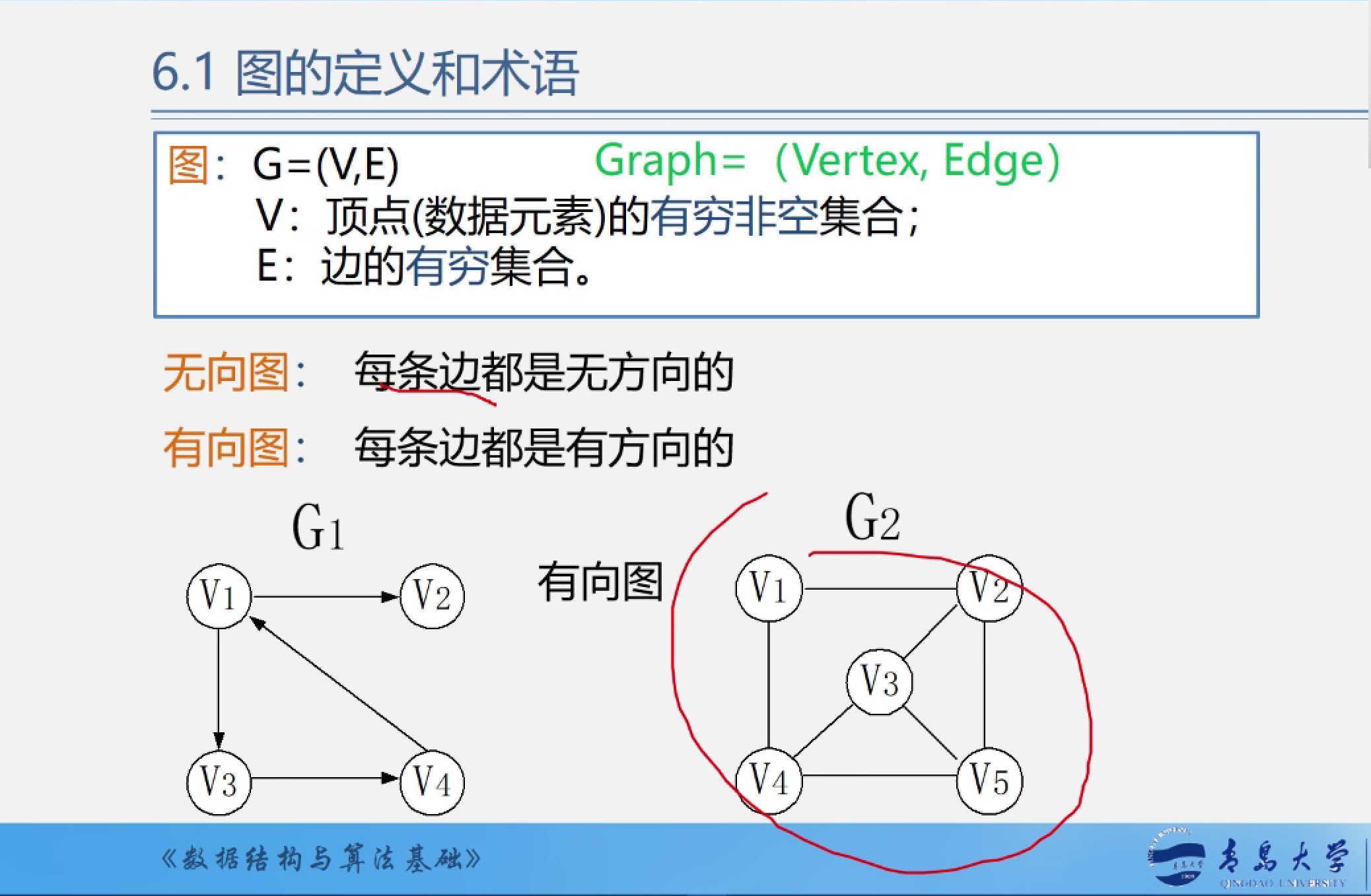
image-20230619092240135

完全图:任意两个点都有一条边相连.

无向完全图:n个顶点,至少n(n-1)/2条边.

有向完全图:n个顶点,至少n(n-1)条边.

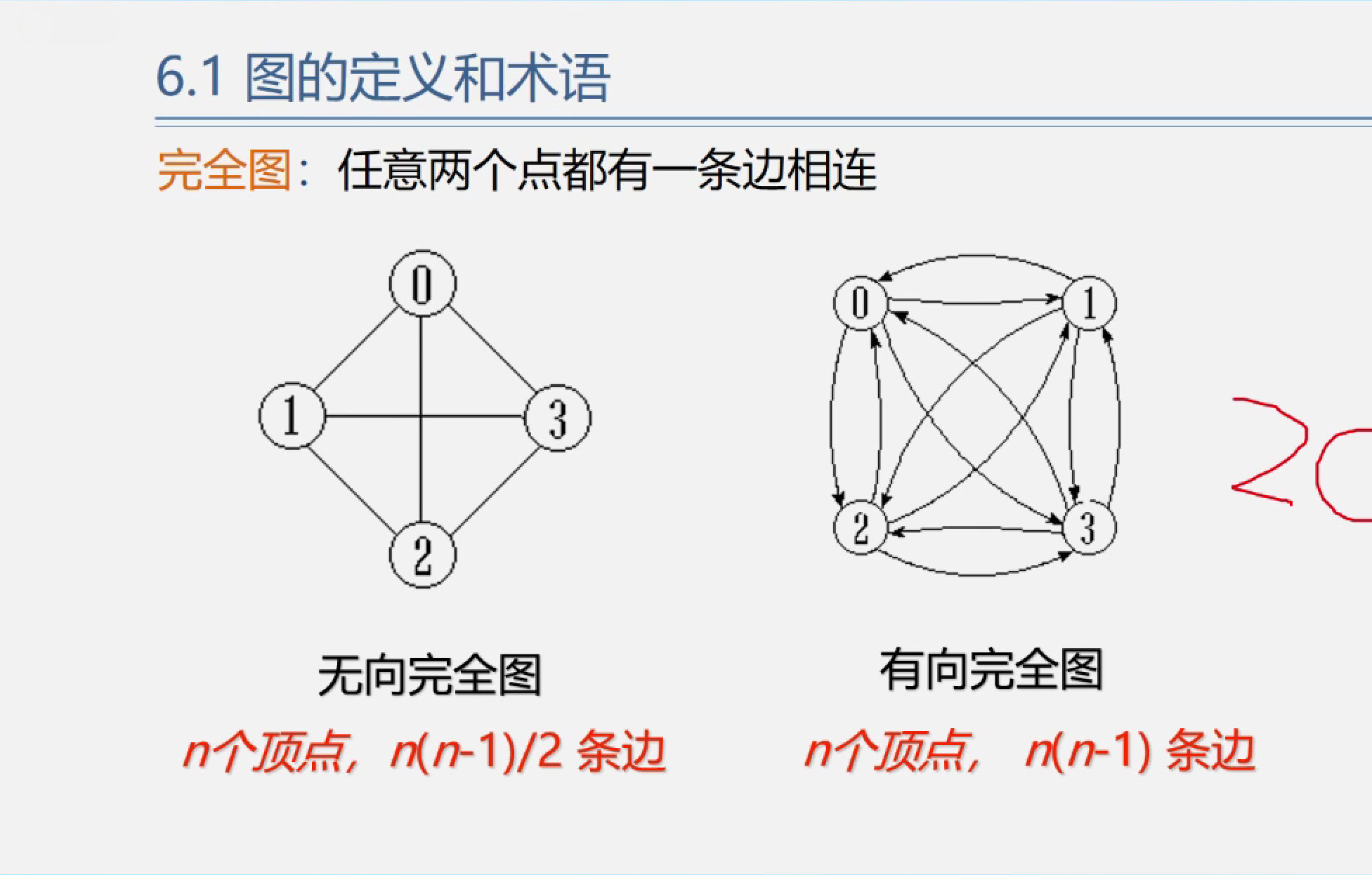
image-20230619092639482

稀疏图:有很少边或弧(带箭头的边)的图.

稠密图:有较多边或弧的图.

网:边/弧带权的图.

邻接:有边/弧相连的两个顶点之间的关系.

关联(依附):边/弧与顶点之间的关系.

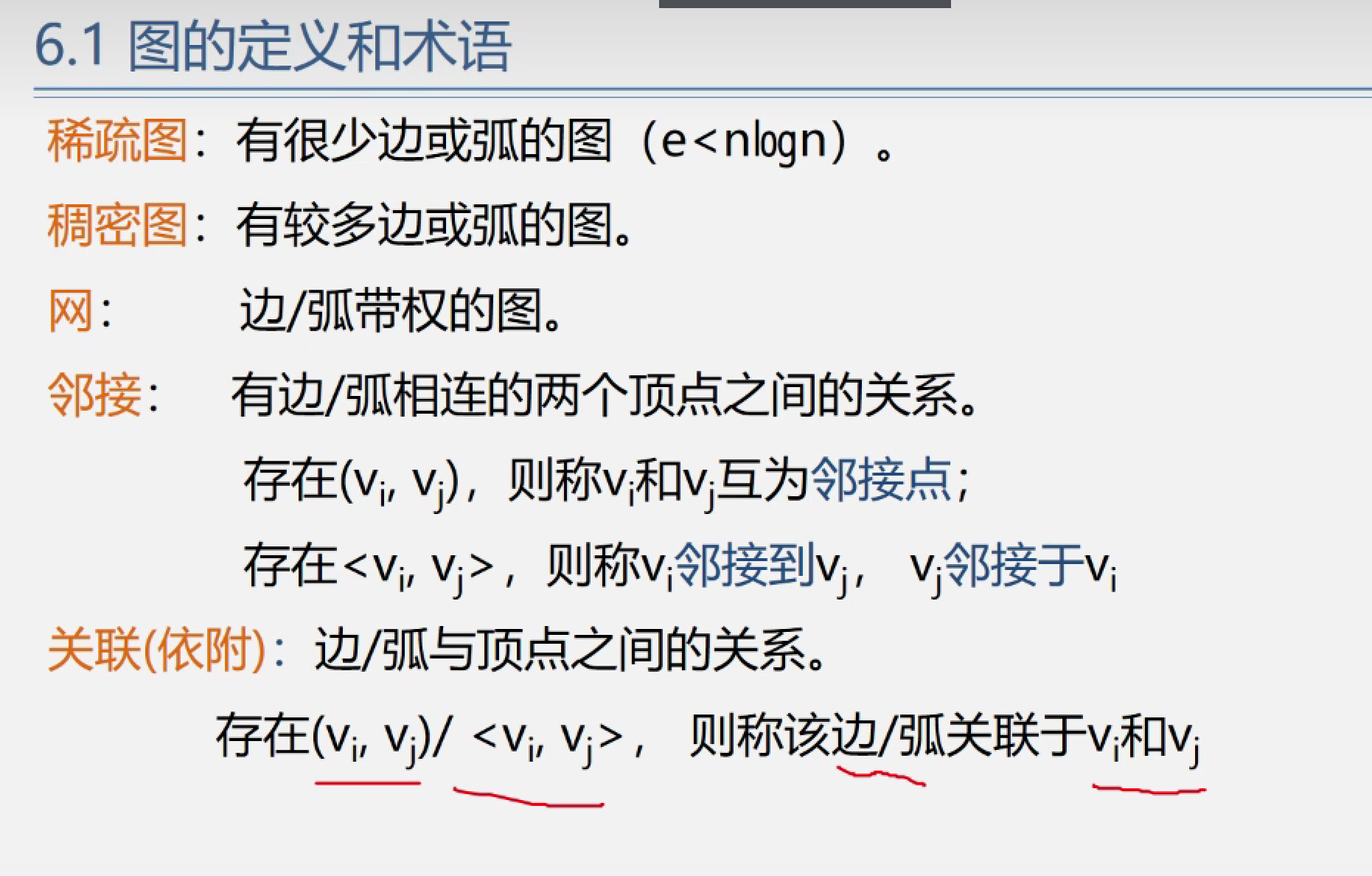
image-20230619093204088

顶点的度:与顶点相关联的边的数目.

有向图中,顶点的度等于顶点的入度和出度之和.

image-20230619093512835

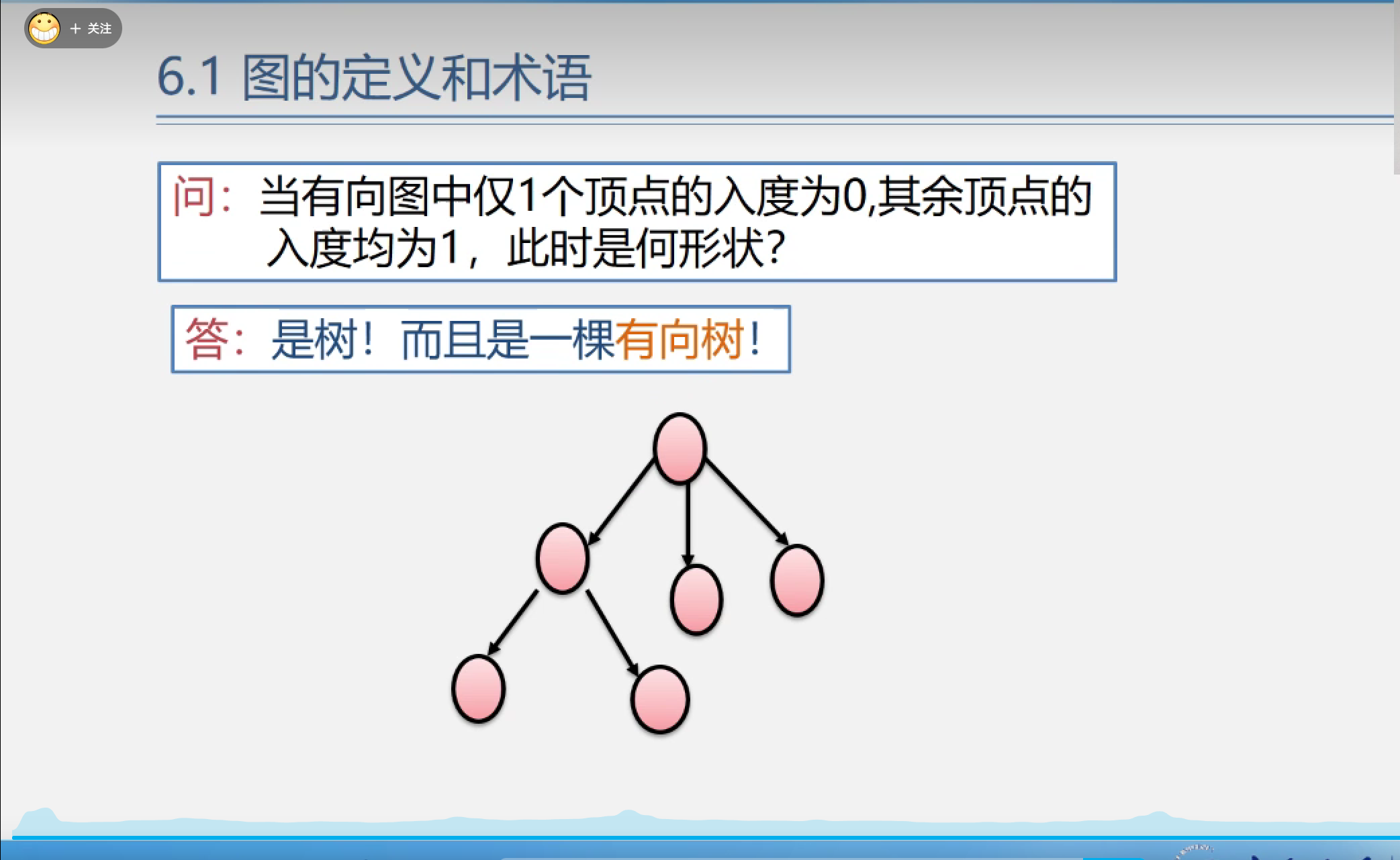
image-20230619093646747

路径:接续的边构成的顶点序列.

路径长度:路径上边或弧的数目/权值之和.

回路(环):第一个顶点和最后一个顶点相同.

简单路径:除路径起点和终点相同外,其余顶点均不相同的路径.

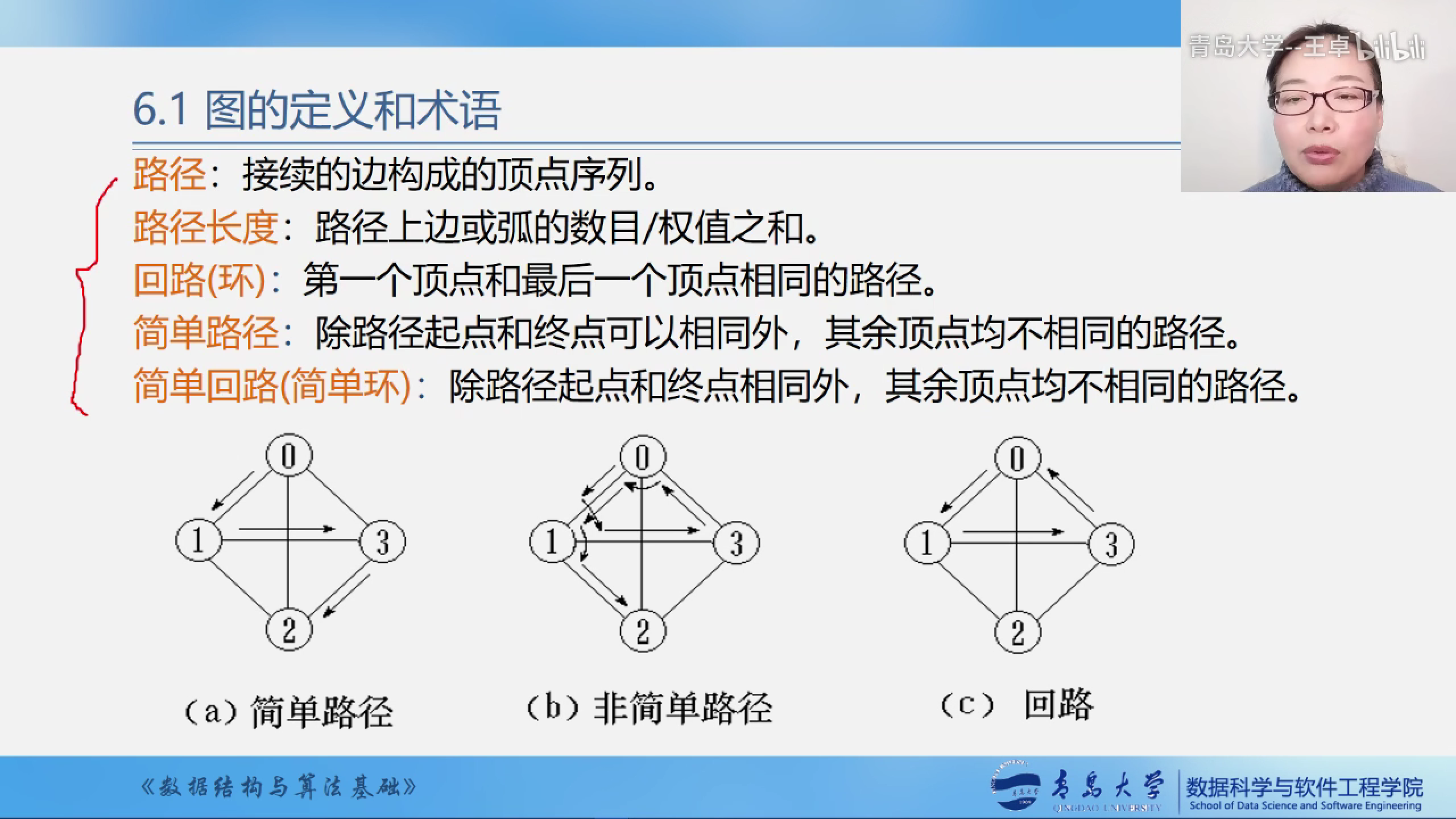
image-20230620092928751

连通图(强连通图):再无(有)向图中,若对任何两个顶点u,v都存在从v,u的路径,则称G是连通图(强连通图).

image-20230620093401974

权和网

图中边或弧所具有的相关树称为权,表明从一个顶点到另一个顶点的距离或耗费.

带权的图就称为网.

image-20230620093534130

子图

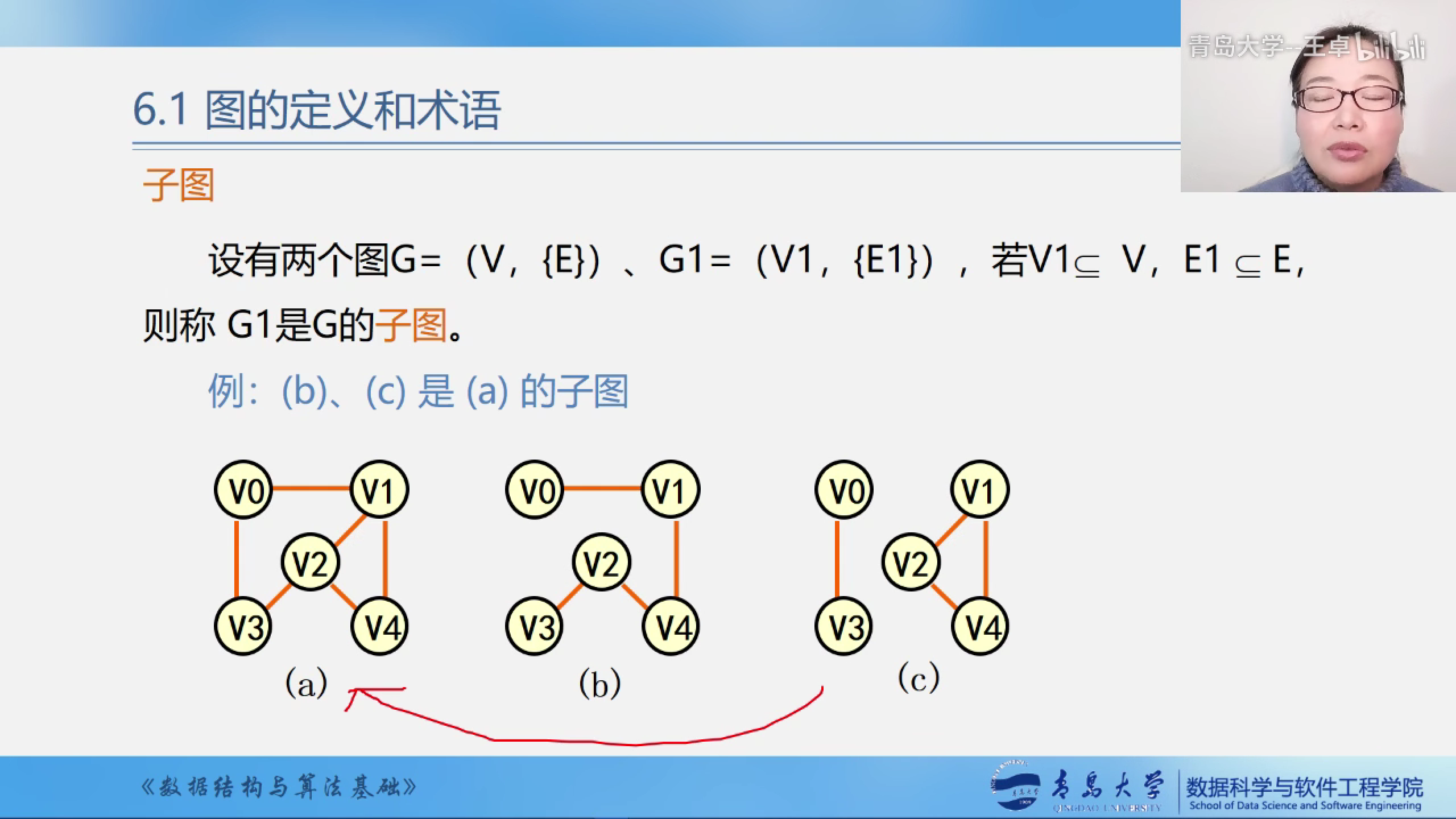
image-20230620093838706

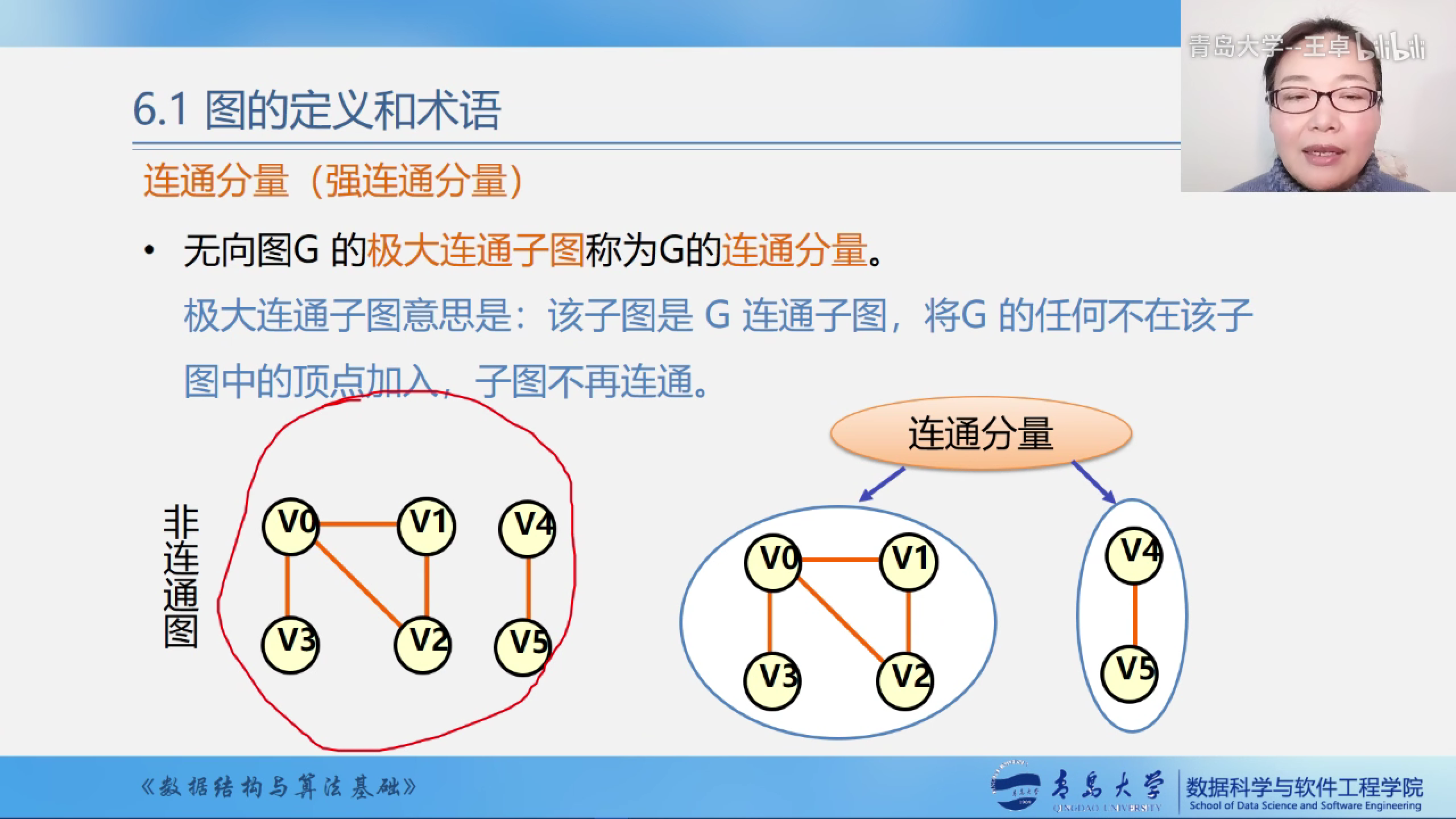
连通分量(强联通分量)

无向图G的极大连通子图称为G的连通分量.

image-20230620094149188

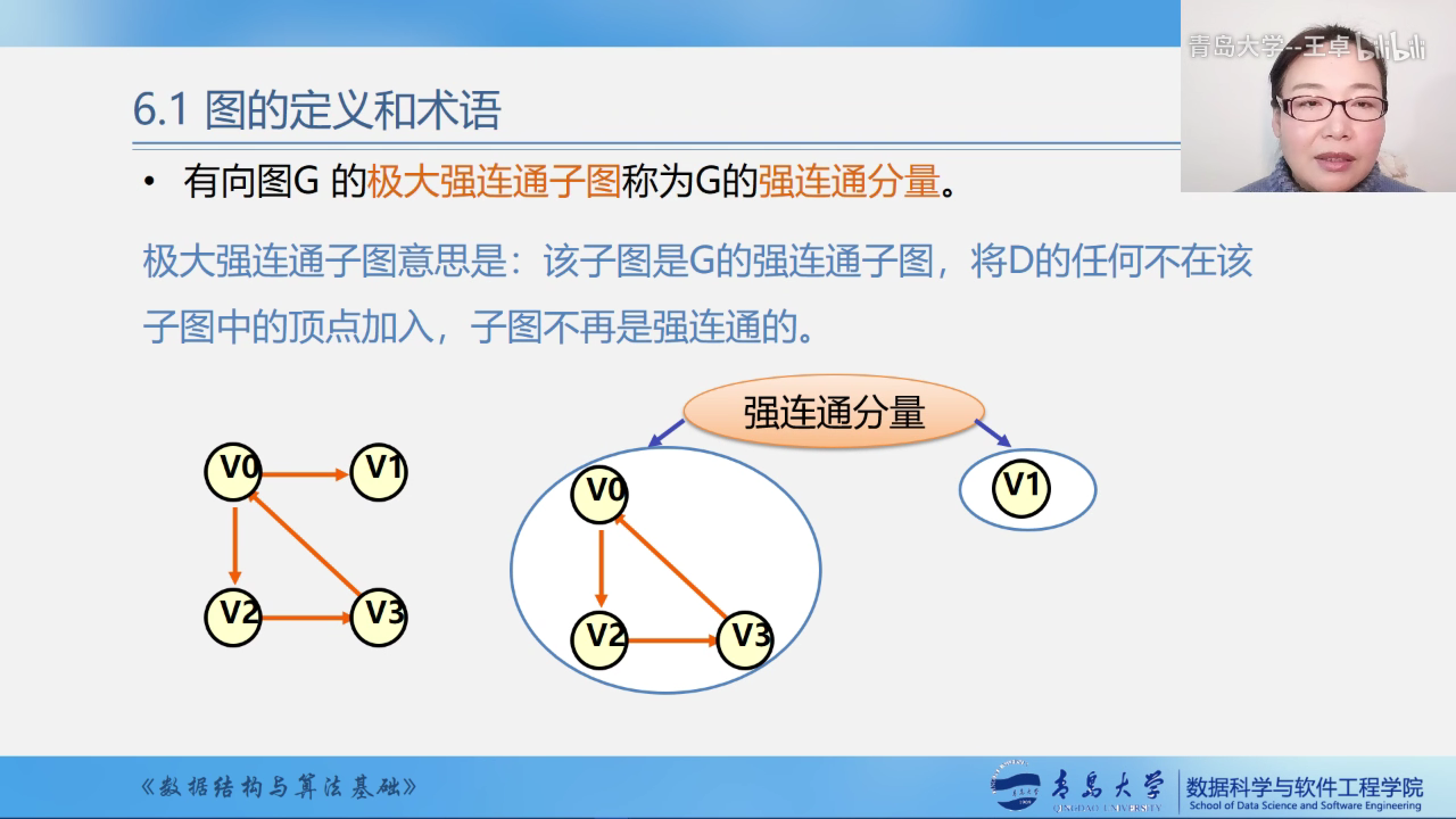
有向图G的极大强连通子图称为G的强连通分量.

image-20230620094410496

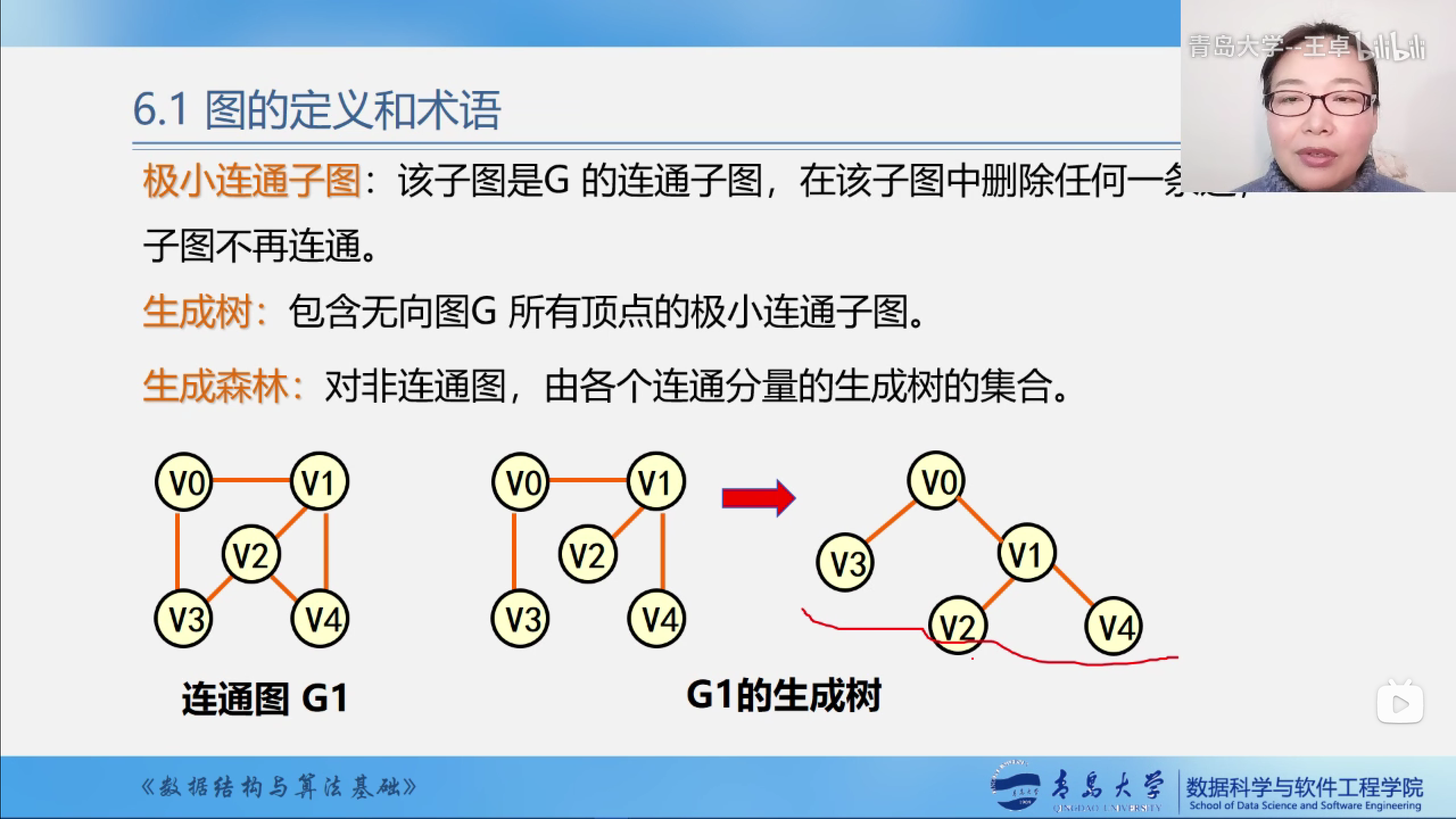
极小连通子图

生成树

生成森林

image-20230620094630946

posted @ 2023-06-19 09:37  harper886  阅读(38)  评论(0)  编辑  收藏  举报