高等数学 5.3 平面及其方程

image-20230222201319049

点法式方程

就是用该平面的法向量和平面内一个点，过法向量n和向量\(M_{0}M\)通过垂直关系建立的一个方程

image-20230222202722958

通过平面上的一个点M和法向量n建立的方程如下

image-20230222202936741

这个例子说明如果知道平面中两个向量可以用这这两个向量的×乘的结果求出平面法向量，进一步使用点法式方程求出平面法向量

image-20230222203244728

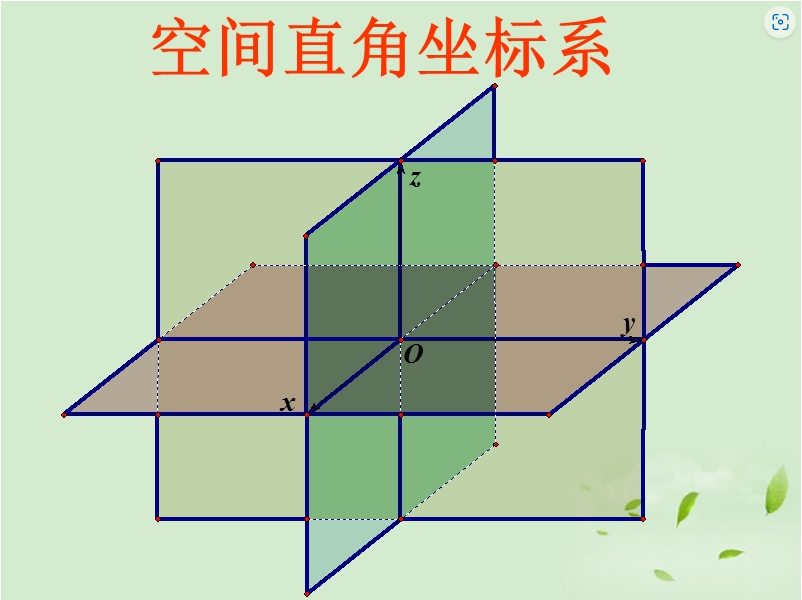
平面的一般方程

任何平面都可以用三元一次方程表示。该平面方程前面的ABC系数可以作为该平面的法向量坐标。\(\vec{n}\) = (A,B,C)

image-20230222203729166

一些特例

image-20230222203849929

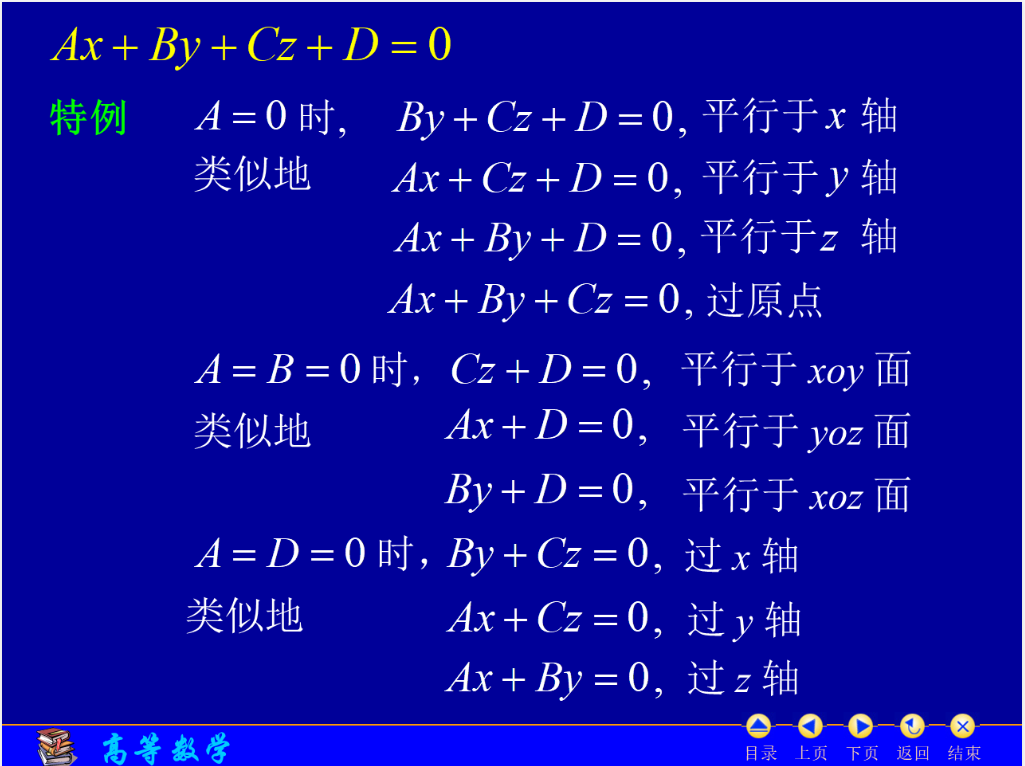
image-20230222203910694

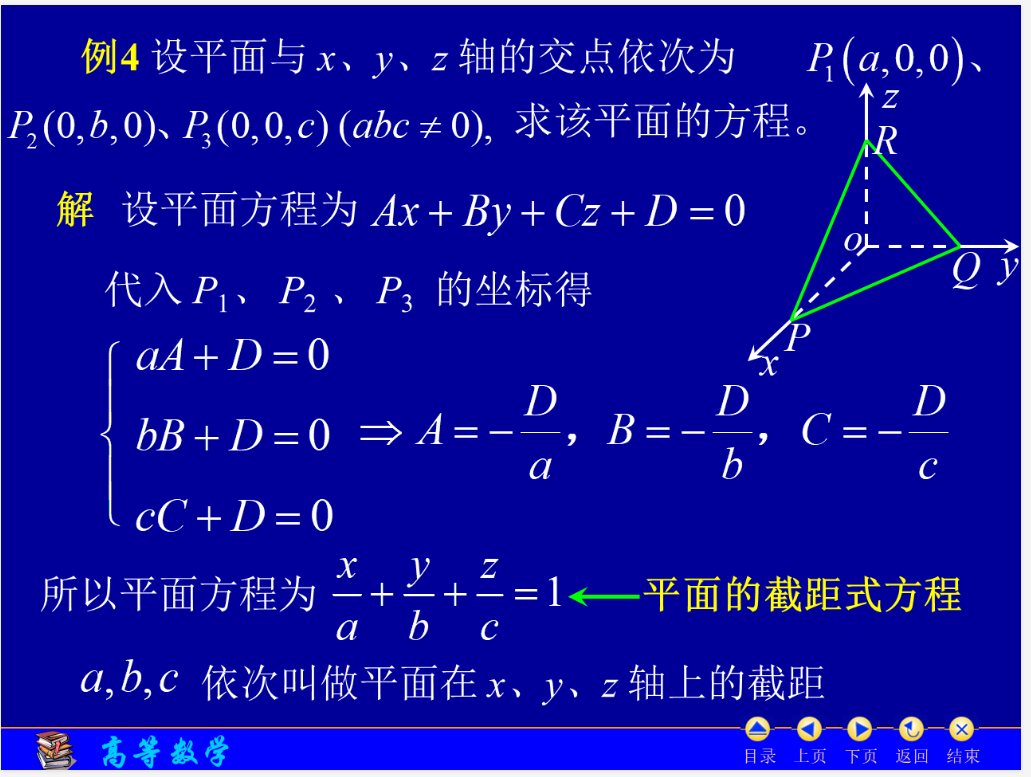
平面的截距式方程

因为图片上的三个点比较特殊都在坐标轴上，设出平面的一般式方程将这三个点带入即可得到这个方程，可以类比直线的截距式方程记忆。

image-20230222204216810

两平面的夹角

可以用两平面的法向量来求出余弦值

image-20230222204855064

两个法向量平行的时候两平面平行，两个法向量垂直的时候两平面垂直.

image-20230222205108186

平面外一点到平面的距离

需要该平面的法向量和平面上一点，距离就是p0和p1点在法向量上面的投影。带入公式计算就可以。

image-20230222205613784

内容回顾

image-20230222205710570

image-20230222205649212

posted @ 2023-02-22 21:00  harper886  阅读(560)  评论(0)    收藏  举报