《概率机器人》课后习题 第3章
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from matplotlib.patches import Circle
第一题
第1问
为了方便，把状态记为\(x\)，位移、速度、加速度分别记为\(s\)、\(v\)、\(a\)。
状态向量为\([s_t,v_t]^T\)，状态转移矩阵为
\[A=\begin{bmatrix}
1&1\\
0&1\\
\end{bmatrix}
\]
第2问
控制量\(u_t\)设为0。近似认为单位时间内速度与加速度都是恒定值，则有
\[\begin{aligned}
&s_{t+1}=s_t+v_{t}+\frac{1}{2}a_{t}\\
&v_{t+1}=v_{t}+a_{t}
\end{aligned}
\]
写成矩阵的形式有
\[x_{t+1}=Ax_{t}+\begin{bmatrix}\frac{1}{2}\\1\end{bmatrix}a_t
\]
进一步可由定义以计算协方差矩阵\(R\)：
\[\begin{aligned}
R&=\begin{bmatrix}
Cov(\frac{1}{2}a_t)&E([\frac{1}{2}a_t-0][a_t-0])\\
E([\frac{1}{2}a_t-0][a_t-0])&Cov(a_t)
\end{bmatrix}\\
&=\begin{bmatrix}
\frac{1}{4}&\frac{1}{2}[Cov(a_t)+E(a_t)^2]\\
\frac{1}{2}[Cov(a_t)+E(a_t)^2]&1
\end{bmatrix}\\
&=\begin{bmatrix}
\frac{1}{4}&\frac{1}{2}\\
\frac{1}{2}&1
\end{bmatrix}
\end{aligned}
\]
可以发现这个结果就是\([\frac{1}{2},1]^T[\frac{1}{2},1]\)，但是我概率论知识不扎实，不知道为什么可以这样算。
故在已知\(x_{t-1}\)的条件上，可以得出\(x_t\)的分布为：
\[p(x_t\mid u_t,x_{t-1})=[\det(2\pi R)]^{-\frac{1}{2}}\exp\left[
-\frac{1}{2}(x_t-Ax_{t-1})^TR^{-1}(x_t-Ax_{t-1})
\right]
\]
注意此时\(R\)是奇异矩阵，这说明这个这时这个多维高斯分布存在多余的维度，回顾一下上一问的状态转移矩阵，可以发现此时\(x_t\)和\(\dot x_t\)都是与\(\ddot x_t\)成比例，因此退化成了一个一维的分布。
进一步，如果\(x_t\)并不是确定值，而是满足\(X_{t-1}\sim \mathcal N(\mu_{t-1}, \Sigma_{t-1})\)，则有\(X_t\sim \mathcal N(\mu_{t}, \Sigma_{t})\)，参数满足：
\[\begin{aligned}
&\mu_t = A_t\mu_{t-1}\\
&\Sigma_{t} = A_t\Sigma_{t-1}A_t^T+R
\end{aligned}
\]
第3问
此时未作测量，只能计算先验估计，关系同上一问最后得出的，即：
\[\begin{aligned}
&\bar\mu_t=A\bar\mu_{t-1}\\
&\bar\Sigma_t=A\bar\Sigma_{t-1}A^T+R
\end{aligned}
\]
初始条件为\(\bar\mu_0=[0],\bar\Sigma=[0]\)，故不难知道均值始终为\([0]\)，只计算方差如下：
A = np.array([[1, 1], [0, 1]])
R = np.array([[1/4, 1/2], [1/2, 1]])
covar = np.zeros((2, 2))
ITER = 5
for i in range(ITER):
covar = np.matmul(np.matmul(A, covar), A.T) + R
print(covar)
[[0.25 0.5 ]
[0.5 1. ]]
[[2.5 2. ]
[2. 2. ]]
[[8.75 4.5 ]
[4.5 3. ]]
[[21. 8.]
[ 8. 4.]]
[[41.25 12.5 ]
[12.5 5. ]]
第4问
x_plot = []
y_plot = []
for theta in np.linspace(0, 2*np.pi, 100):
u = np.array([[np.cos(theta)], [np.sin(theta)]])
sig = np.matmul(np.matmul(u.T, covar), u)
x_plot.append(np.sqrt(sig) * np.cos(theta))
y_plot.append(np.sqrt(sig) * np.sin(theta))
eig, eig_vecs = np.linalg.eig(covar)
print("eigen value is %.4f and %.4f"%(eig[0], eig[1]))
print("corresponding sigma^2 is %.4f and %.4f"
%(np.matmul(np.matmul(eig_vecs[:, 0].T, covar), eig_vecs[:, 0]),
np.matmul(np.matmul(eig_vecs[:, 1].T, covar), eig_vecs[:, 1])))
plt.arrow(0, 0, eig_vecs[0, 0] * np.sqrt(eig[0]), eig_vecs[1, 0] * np.sqrt(eig[0]),
width=0.1, head_width=0.3, length_includes_head=True, color='red')
plt.arrow(0, 0, eig_vecs[0, 1] * np.sqrt(eig[1]), eig_vecs[1, 1] * np.sqrt(eig[1]),
width=0.1, head_width=0.3, length_includes_head=True, color='purple')
plt.scatter(x_plot, y_plot, 2)
plt.grid()
plt.gca().set_aspect('equal')
plt.show()
eigen value is 45.1424 and 1.1076
corresponding sigma^2 is 45.1424 and 1.1076
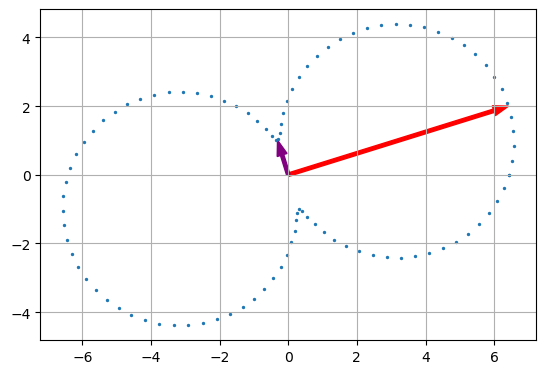
然而这个东西（每个方向上一个数据点投影后的标准差）并不是椭圆😅。。。查了一下定义，大多数说法都是：不确定性椭圆（uncertainty ellipse）是多元高斯的概率密度函数等高线。概率机器人教材上的下边这句话看来有点问题，混淆的主要原因还在于二维高斯分布的标准差没有一个明确的定义：
For each posterior, you are asked to plot an uncertainty ellipse, which is the ellipse of points that are one standard deviation away from the mean.
反正还是继续把等高线画了吧。按照协方差笔记中的讨论，椭圆等高线长短轴方向和特征向量一致，大小和特征值开方一致，中心在均值处就好了。
covar = np.zeros((2, 2))
covars = []
for i in range(ITER):
covar = np.matmul(np.matmul(A, covar), A.T) + R
covars.append(covar)
# https://matplotlib.org/stable/gallery/color/named_colors.html
colors = ['skyblue', 'mediumseagreen', 'lightcoral', 'sandybrown', 'violet']
for i in range(ITER):
covar = covars[ITER-1-i]
eig, eig_vecs = np.linalg.eig(covar)
angle = np.arctan2(eig_vecs[1, 0], eig_vecs[0, 0])
ell = Ellipse((0, 0), np.sqrt(eig[0]), np.sqrt(eig[1]), angle * 180 / np.pi,
label = 'iter: %d'%(ITER-i), facecolor = colors[i])
ax = plt.gca()
ax.add_patch(ell)
ax.set_aspect('equal')
plt.gca().axvline(c='grey', lw=1)
plt.gca().axhline(c='grey', lw=1)
plt.gca().set_aspect('equal')
plt.xlim((-3.5, 3.5))
plt.ylim((-3.5, 3.5))
plt.legend()
plt.show()
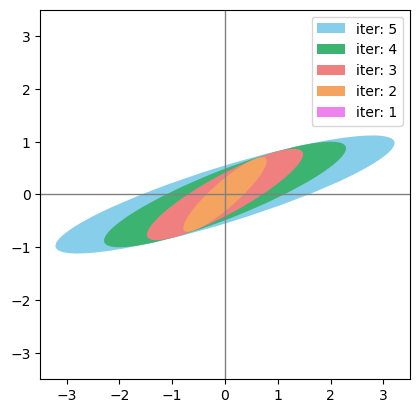
第5问
covar = np.zeros((2, 2))
for i in range(100000):
covar = np.matmul(np.matmul(A, covar), A.T) + R
corre = covar[1, 0] / np.sqrt(covar[0, 0] * covar[1, 1])
if i+1 in [1, 10, 100, 1000, 10000, 100000]:
print("%d: %f"%(i+1, corre))
1: 1.000000
10: 0.867110
100: 0.866036
1000: 0.866026
10000: 0.866025
100000: 0.866025
最后一个该是稳定在0.866025左右了，但是理论上不知道怎么证明这一点😓
第二题
第1问
\[C = \begin{bmatrix}1&0\end{bmatrix}\\
Q = 10
\]
第2问
下边的代码中用了一个变量
scale来缩放椭圆的长短轴，其取值来自参考中的第一个，我用随机生成的数据验证了一下参考中的pdf：SAMPLE = 100000 x_white = np.random.normal(0, 1.0, SAMPLE) y_white = np.random.normal(0, 1.0, SAMPLE) cnt = 0 radius = np.sqrt(5.99) for i in range(SAMPLE): r = np.sqrt(x_white[i] ** 2 + y_white[i] ** 2) if r < radius: cnt += 1 print(cnt)结果是得到\(95040\)，所以其将长短轴拉伸\(\sqrt{5.99}\)（也即长短轴应该取\(\sqrt{5.99\lambda}\)）以使得\(95\%\)的数据会落入椭圆中的结论多半是正确的。但是他的pdf中的椭圆的拉伸貌似并没有取\(\sqrt{5.99}\)，而是取的\(5.99\)，画出来的图也就和下边的不一样了。估计是一点小错误吧。
def measurement_update(bar_mu, bar_sigma, z):
global A, R, C, Q
if type(z) == int or type(z) == float:
# numpy求逆的运算在处理0维的数据时无法直接转换为除法
# 所以这里手动处理一下
kalman_gain = np.matmul(bar_sigma, C.T) \
/ (np.matmul(C, np.matmul(bar_sigma, C.T)) + Q)
else:
kalman_gain = np.matmul(bar_sigma,
np.matmul(C.T, np.linalg.inv(
np.matmul(C, np.matmul(bar_sigma, C.T)) + Q)))
mu = bar_mu + np.matmul(kalman_gain, z
- np.matmul(C, bar_mu))
sigma = np.matmul(
np.eye(kalman_gain.ndim) - np.matmul(kalman_gain, C),
bar_sigma)
return mu, sigma
def draw_2d_uncertainty_ellipse(sigma, mu, scale=1, **kargs):
eig, eig_vecs = np.linalg.eig(sigma)
angle = np.arctan2(eig_vecs[1, 0], eig_vecs[0, 0])
a = np.sqrt(eig[0]) * scale
b = np.sqrt(eig[1]) * scale
ell = Ellipse((mu[0], mu[1]), a, b, angle * 180 / np.pi,
**kargs)
ax = plt.gca().add_patch(ell)
return eig, eig_vecs
# 测量模型的参数
C = np.array([[1, 0]])
Q = 10
# 状态估计迭代5次
sigma = np.zeros((2, 2))
for i in range(5):
sigma = np.matmul(np.matmul(A, sigma), A.T) + R
# 测量模型更新
mu = np.array([[0], [0]])
meas = np.array(5)
mu_update, sigma_update = measurement_update(mu, sigma, meas)
# 画误差椭圆
scale = np.sqrt(5.99) # 拉伸椭圆以使得95%的数据落入椭圆中，取值来自pptacher的笔记
print("=====before update=====")
print("mu:", mu, sep='\n')
print("sigma:", sigma, sep='\n')
eig_values, eig_vecs = draw_2d_uncertainty_ellipse(sigma, mu, scale,
color='skyblue', label='before update', alpha=0.6)
print("eigen values:", eig_values)
print("eigen vectors:", eig_vecs, sep='\n')
print("=====after update=====")
print("mu:", mu_update, sep='\n')
print("sigma:", sigma_update, sep='\n')
eig_values, eig_vecs = draw_2d_uncertainty_ellipse(sigma_update, mu_update, scale,
color='mediumseagreen', label='after update', alpha=0.6)
print("eigen values:", eig_values)
print("eigen vectors:", eig_vecs, sep='\n')
plt.gca().axvline(c='grey', lw=1)
plt.gca().axhline(c='grey', lw=1)
plt.gca().set_aspect('equal')
plt.xlim((-10, 10))
plt.ylim((-5, 5))
plt.legend()
plt.show()
=====before update=====
mu:
[[0]
[0]]
sigma:
[[41.25 12.5 ]
[12.5 5. ]]
eigen values: [45.14239369 1.10760631]
eigen vectors:
[[ 0.95478081 -0.29731062]
[ 0.29731062 0.95478081]]
=====after update=====
mu:
[[4.02439024]
[1.2195122 ]]
sigma:
[[8.04878049 2.43902439]
[2.43902439 1.95121951]]
eigen values: [8.90434405 1.09565595]
eigen vectors:
[[ 0.94362832 -0.33100694]
[ 0.33100694 0.94362832]]
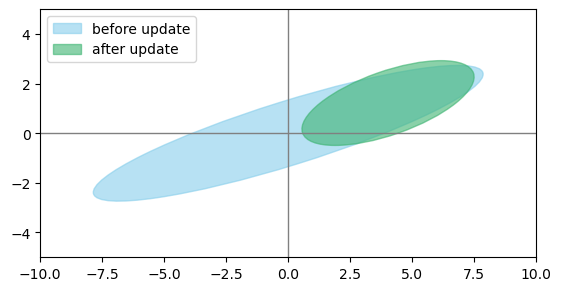
第三题
这一块并不是很了解，涉及到多维随机变量的特征函数。看pptacher前辈的思路，大概还是利用和一维特征函数一样的性质来解答这题的：①特征函数与分布一一对应；②随机变量求和后的新分布对应的特征函数等于原随机变量的特征函数之积。具体还是看pptacher的pdf吧。
第四题
第1问
理解这题花了不少时间，我理解它的意思是：用自己找得到的最好的方式，给出在初态条件上往前走单位长度之后的状态概率分布。题中给出了预测模型：
\[\begin{bmatrix}
x_{t}\\ y_{t}\\ \theta_{t}
\end{bmatrix}
=\boldsymbol g(\mu_{t-1})
=\begin{bmatrix}
x_{t-1}+\cos(\theta_{t-1})\\
y_{t-1}+\sin(\theta_{t-1})\\
\theta_{t-1}
\end{bmatrix}
\]
需要注意的是本题的初态是一个估计而不是一个确定量。解析解我仍然不会，但参考中pptacher前辈给出了他的答案。我就尝试使用一些随机的点来模拟一下啦：
SAMPLE=200
x = np.random.normal(0, 0.1, SAMPLE)
y = np.random.normal(0, 0.1, SAMPLE)
theta = np.random.normal(0, 100, SAMPLE)
x_1 = []
y_1 = []
for i in range(SAMPLE):
x_1.append(x + np.cos(theta))
y_1.append(y + np.sin(theta))
plt.gca().axvline(c='grey', lw=1)
plt.gca().axhline(c='grey', lw=1)
plt.gca().set_aspect('equal')
plt.scatter(x, y, s=3, c='seagreen', label='initial')
plt.scatter(x_1, y_1, s=3, c='skyblue', label='after')
plt.legend()
plt.show()
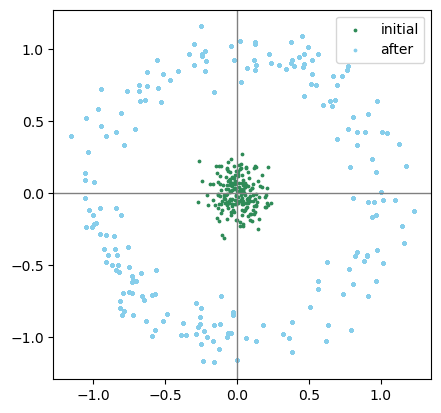
不管怎么说，这个东西（天蓝色）至少不是高斯分布。
第2、3问
\(g\)在上一小问中已给出，对其求偏导可以得到\(G_t\)：
\[\begin{aligned}
G_t &= \frac{\partial \boldsymbol g}{\partial \boldsymbol{x_{t-1}}}\\
&=\begin{bmatrix}
1&0&-\sin(\theta_{t-1})\\
0&1&\cos(\theta_{t-1})\\
0&0&1
\end{bmatrix}
\end{aligned}
\]
def ekf_predict(mu_pre, sigma_pre):
global G
mu = mu_pre + np.array([[np.cos(theta)], [np.sin(theta)], [0]])
sigma = np.matmul(G, np.matmul(sigma_pre, G.T))
return mu, sigma
mu = np.zeros((3, 1))
sigma = np.diag([0.01, 0.01, 10000])
G = np.eye(3)
theta = mu[2, 0]
G[0, 2] = -np.sin(theta)
G[1, 2] = np.cos(theta)
mu_predict, sigma_predict = ekf_predict(mu, sigma)
print("predicted mu:", mu_predict, sep='\n')
print("predicted sigma:", sigma_predict, sep='\n')
# 画不确定性椭圆
draw_2d_uncertainty_ellipse(sigma_predict[:2, :2], mu_predict[:2],
np.sqrt(5.99), label='ekf predict', alpha=0.8, color='skyblue')
plt.gca().axvline(c='grey', lw=1)
plt.gca().axhline(c='grey', lw=1)
plt.gca().set_aspect('equal')
plt.xlim((-0.5, 1.5))
plt.ylim((-1, 1))
plt.legend()
plt.show()
predicted mu:
[[1.]
[0.]
[0.]]
predicted sigma:
[[1.000000e-02 0.000000e+00 0.000000e+00]
[0.000000e+00 1.000001e+04 1.000000e+04]
[0.000000e+00 1.000000e+04 1.000000e+04]]
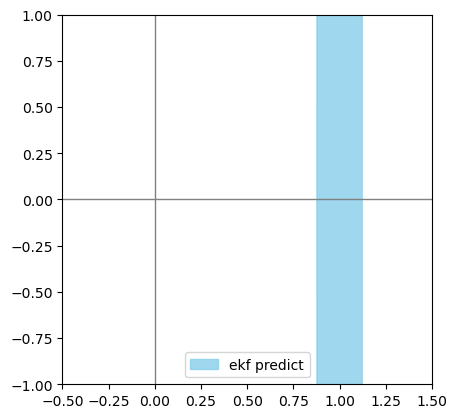
对比1问中模拟的结果，这个结果可以说是相当不靠谱的了，可见EKF应该只在部分场景下才有效。
第4问
def ekf_update(mu_predict, sigma_predict, z):
global H, Q
# 1维测量值，不用求逆
kalman_gain = np.matmul(sigma_predict, H.T) \
/ (np.matmul(H, np.matmul(sigma_predict, H.T)) + Q)
mu_update = mu_predict + kalman_gain * (z - np.matmul(H, mu_predict))
sigma_update = np.matmul(
np.eye(sigma_predict.shape[0]) - np.matmul(kalman_gain, H),
sigma_predict)
return mu_update, sigma_update
MEAS_SAMPLE = 50
H = np.array([[1, 0, 0]]) # 线性测量模型
Q = 0.01
meas = np.linspace(0, 2, MEAS_SAMPLE) # 测量值
x_post = []
for i in range(MEAS_SAMPLE):
z = meas[i]
mu_update, sigma_update = ekf_update(mu_predict, sigma_predict, z)
x_post.append(mu_update[0, 0])
plt.plot(meas, x_post, c='skyblue')
plt.gca().set_aspect('equal')
plt.grid()
plt.show()
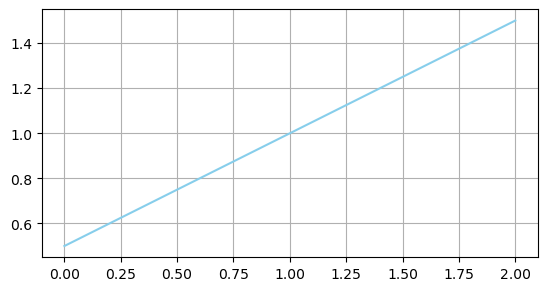
第5问
因为我的模型没法用，所以只能考虑一下初始角度已知，但是\(y\)未知的情况。
mu = np.zeros((3, 1))
sigma = np.diag([0.01, 10000, 0])
mu_predict, sigma_predict = ekf_predict(mu, sigma)
print("linearize measurement matrix:", G, sep='\n')
print("predicted mu:", mu_predict, sep='\n')
print("predicted sigma:", sigma_predict, sep='\n')
# 画不确定性椭圆
draw_2d_uncertainty_ellipse(sigma_predict[:2, :2], mu_predict[:2],
np.sqrt(5.99), label='ekf predict', alpha=0.8, color='skyblue')
plt.gca().axvline(c='grey', lw=1)
plt.gca().axhline(c='grey', lw=1)
plt.gca().set_aspect('equal')
plt.xlim((-0.5, 1.5))
plt.ylim((-1, 1))
plt.legend()
plt.show()
linearize measurement matrix:
[[ 1. 0. -0.]
[ 0. 1. 1.]
[ 0. 0. 1.]]
predicted mu:
[[1.]
[0.]
[0.]]
predicted sigma:
[[1.e-02 0.e+00 0.e+00]
[0.e+00 1.e+04 0.e+00]
[0.e+00 0.e+00 0.e+00]]
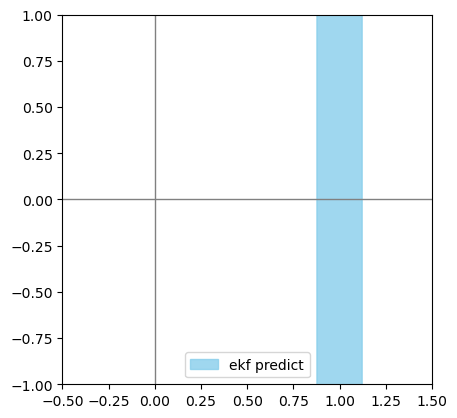
此处设\(Y\)的方差与之前\(\theta\)的一样，以表示不确定\(y\)的初始值，然后得到的结果和之前角度不确定的也几乎一模一样。观察一下\(G\)，会发现它在改变\(Y\)的方差时，\(Y\)的方差与\(\theta\)的方差具有一样的权重，因此造成了这个巧合。
第五题
新的运动模型和测量模型为
\[x_t = A_tx_{t-1}+B_tu_{t}+c_1+\boldsymbol\varepsilon_t\\
z_t = C_tx_t +c_2+\delta_t
\]
偏移量是定值，因此不应改变方差，另外还可以定义新的测量结果为\(z'=z - c_2\)，于是可以得到新的算法为：
-
做出估计
\[\begin{aligned} &\bar{\mu}_t=A_t \mu_{t-1}+B_t u_t +c_1\\ &\bar{\Sigma}_t=A_t \Sigma_{t-1} A_t^T+R_t \\ \end{aligned} \] -
更新估计
\[\begin{aligned} &K_t=\bar{\Sigma}_t C_t^T\left(C_t \bar{\Sigma}_t C_t^T+Q_t\right)^{-1} \\ &\mu_t=\bar{\mu}_t+K_t\left(z_t-c_2-C_t \bar{\mu}_t\right) \\ &\Sigma_t=\left(I-K_t C_t\right) \bar{\Sigma}_t \end{aligned} \]
第六题
这一小题要求举出一个稀疏信息矩阵的实例，并凭实例说明系数的信息矩阵意味着各个变量之间的相关系数都非常接近1。
可是最简单的例子就是单位矩阵\(I\)，这个矩阵对应的协方差矩阵也是单位矩阵，可是协方差矩阵为单位矩阵就意味着各个变量间的相关系数都是0🤨这题没弄不清楚。
