多元高斯分布的协方差矩阵

看《概率机器人》时总是遇到这个协方差矩阵，但对这家伙一直没有个直观认识，因此集中学一下，同时顺带捡起来一点点线代知识。

定义

设待讨论的随机变量\(X_i\)构成随机向量\(\boldsymbol X = [X_1, X_2, \cdots, X_n]^T\)，则协方差矩阵定义为一个\(n\times n\)矩阵\(\Sigma\)，其第\(i\)行\(j\)列的元素为

\[\Sigma_{ij}=\operatorname{Cov}(X_i, X_j) \]

现实中的协方差矩阵是基于对随机变量的采样数据进行计算而得到的，假设每一次对\(n\)个随机变量进行采样，进而构成随机向量，并且共进行了\(k\)次采样，第i次的结果记为\(\boldsymbol{x_i}=[x_i1,x_i2,\cdots,x_in]^T\)，则协方差矩阵计算如下

\[\Sigma = \frac{1}{k}\sum\limits_{i=1}^n(\boldsymbol x_i-\boldsymbol{\bar x})(\boldsymbol x_i-\boldsymbol{\bar x})^T \]

从中还可以看出，如果对随机向量进行线性变换\(T\)，则协方差矩阵会变为\(T\Sigma T^T\)（注意是后边那个做的转置）。

性质

对称

由定义直接可以得到。

线代拾遗

实对称矩阵的特征向量相互正交。
假设实对称矩阵\(A\)满足\(A\boldsymbol u_1=\lambda_1\boldsymbol u_1\)、\(A\boldsymbol u_2=\lambda_2\boldsymbol u_2\)，则有

\[\boldsymbol u_2^T A\boldsymbol u_1=\lambda_1\boldsymbol u_2^T\boldsymbol u_1\\ =(\boldsymbol u_1^T A\boldsymbol u_2)^T=(\lambda_1\boldsymbol u_2^T\boldsymbol u_1)^T=\lambda_1\boldsymbol u_2^T\boldsymbol u_1 \]
因为\(\lambda_1\ne\lambda_2\)，所以必有\(\boldsymbol u_2^T\boldsymbol u_1=0\)，即两特征向量正交。

各列向量为单位向量且互相正交的矩阵（也称为正交矩阵）的逆就是其本身的转置。

假设\(A\)的各列正交且为单位向量，则计算一下即可发现\(A^TA=I\)。后边解释协方差矩阵可以拆成一个矩阵和其转置相乘时会用到这一点。

半正定

根据定义，协方差矩阵可由下式计算

\[\Sigma = E[(\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^T] \]

故对于任意与\(\boldsymbol{x}\)具有相同个数元素的向量\(u\)

\[\begin{aligned} u^T\Sigma u &= E[(u^T\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^Tu]\\ &=E\{[u^T(\boldsymbol{x}-\boldsymbol{\mu})]^2\}\\ &\ge0 \end{aligned} \]

即可得多元高斯分布的协方差矩阵具有半正定的性质。

在浏览有关协方差矩阵的材料中，经常可以看到一些假定协方差矩阵正定（同时也会满秩）的操作，这其实不是一定的（尽管大多数情况下还是会正定），参考[1]。

现在展开说一说，对于\(n\)维非零随机向量\(\boldsymbol u\)，做如下操作

\[\begin{aligned} \boldsymbol u^T\Sigma\boldsymbol u &=\frac{1}{k}\sum\limits_{i=1}^n\boldsymbol u^T(\boldsymbol x_i-\boldsymbol{\bar x})(\boldsymbol x_i-\boldsymbol{\bar x})^T\boldsymbol u\\ &=\frac{1}{k}\sum\limits_{i=1}^n[(\boldsymbol x_i-\boldsymbol{\bar x})^T\boldsymbol u]^T(\boldsymbol x_i-\boldsymbol{\bar x})^T\boldsymbol u\\ &=\frac{1}{k}\sum\limits_{i=1}^n(\boldsymbol z_i^T \boldsymbol u)^2\\ \end{aligned} \]

其中\(\boldsymbol z_i=\boldsymbol x_i-\boldsymbol{\bar x}\)，故\(\boldsymbol u^T\Sigma\boldsymbol u\)为0的充要条件为\(\boldsymbol z_i^T \boldsymbol u=0\)。

现假设\(\boldsymbol u^T\Sigma\boldsymbol u=0\)，且\(\operatorname{span}(\boldsymbol z_1,\boldsymbol z_2,\cdots,\boldsymbol z_k)=\R^n\)，则\(u\)可以表示为\(\boldsymbol u=\alpha_1 \boldsymbol z_1+\alpha_2 \boldsymbol z_2+\cdots+\alpha_k \boldsymbol z_k\)，继而可得到

\[\boldsymbol u^T\boldsymbol u=\alpha_1 \boldsymbol z_1^T\boldsymbol u+\alpha_2 \boldsymbol z_2^T\boldsymbol u+\cdots+\alpha_k \boldsymbol z_k^T\boldsymbol u=0 \]

这说明\(\boldsymbol u=0\)，与前提条件矛盾，故\(\operatorname{span}(\boldsymbol z_1,\boldsymbol z_2,\cdots,\boldsymbol z_k)=\R^n\)时基于采样数据计算得到的协方差矩阵即会正定，也即\(\operatorname{rank}(\boldsymbol z_1,\boldsymbol z_2,\cdots,\boldsymbol z_k)=n\)时即正定。当采样数据足够多时，这一条件是不难达成的，因此大多数实际情况中协方差矩阵应是正定的。

线代拾遗

正定矩阵的特征值均为正数。

假定正定矩阵\(A\)满足\(A\boldsymbol u=\lambda\boldsymbol u\)，则\(\boldsymbol u^TA\boldsymbol u=\lambda\boldsymbol u^T\boldsymbol u>0\)，因为\(\boldsymbol u^T\boldsymbol u>0\)，故\(\lambda>0\)。

可拆成一个矩阵和其转置相乘

假设采样数据足够多，则协方差矩阵正定，正定则也就满秩，因此可对其进行相似对角化：

\[\begin{aligned} \Sigma&=U\Lambda U^{-1}\\ &=U\Lambda^{\frac{1}{2}}\Lambda^{\frac{1}{2}}U^{T}\\ &=(U\Lambda^{\frac{1}{2}})(U\Lambda^{\frac{1}{2}})^T\\ &=TT^T \end{aligned} \]

有了这一性质，一般的多维高斯分布都可以看作是标准多为高斯分布的线性变换再加上一个均值向量，其中线性变换就是上边的\(T\)，均值向量就是\(\boldsymbol\mu\)。

协方差矩阵特征向量、特征值的几何意义

意义1：投影到一维后具有极值标准差

先说结论：随机向量在新协方差矩阵特征向量方向上的投影（这是一个新的一维随机变量），相比于在其他方向上的投影，取到了方差的极值，并且该极值就是该特征向量对应的特征值。

注意：如果把各个方向上一倍标准差上取点并连线，得到的并不是一个椭圆（因为《概率机器人》习题中的描述我一度误以为这应该是个椭圆）。

然后从理论上证明一下：设\(X\sim \mathcal N(\boldsymbol\mu, \Sigma)\)，则采样数据在单位\(\omega\)方向上的投影的方差为：

\[\begin{aligned} \sigma^2 &=\frac{1}{n}\sum\limits_i^k[\boldsymbol\omega^T(\boldsymbol x_i-\boldsymbol\mu)]^2\\ &=\frac{1}{n}\sum\limits_i^k[\boldsymbol\omega^T(\boldsymbol x_i-\boldsymbol\mu)][\boldsymbol\omega^T(\boldsymbol x_i-\boldsymbol\mu)]^T\\ &=\frac{1}{n}\sum\limits_i^k\boldsymbol\omega^T(\boldsymbol x_i-\boldsymbol\mu)^2\boldsymbol\omega\\ &=\boldsymbol\omega^T\left[\frac{1}{k}\sum\limits_{i=1}^n(\boldsymbol x_i-\boldsymbol{\bar x})(\boldsymbol x_i-\boldsymbol{\bar x})^T\right]\boldsymbol\omega\\ &=\boldsymbol\omega^T\Sigma \boldsymbol\omega \end{aligned} \]

求在\(\boldsymbol\omega^T\boldsymbol\omega=1\)的条件上令\(\sigma^2\)取极值的\(\omega\)，可以通过拉格朗日乘数法构造一个目标函数：

\[L(\omega,\lambda)=\boldsymbol\omega^T\Sigma \boldsymbol\omega+\lambda(1-\boldsymbol\omega^T\boldsymbol\omega) \]

对其求偏导并令偏导为0，可以得到取极值的条件：

\[\frac{\partial L(\omega,\lambda)}{\partial \omega}=2\boldsymbol\omega^T\Sigma+2\lambda\boldsymbol\omega^T =0\\ \Leftrightarrow\Sigma\boldsymbol\omega=\lambda\boldsymbol\omega \]

即有\(\boldsymbol\omega\)是\(\Sigma\)的特征向量。将该结论带回上式，可以得到此时还满足\(\sigma^2=\lambda\)。

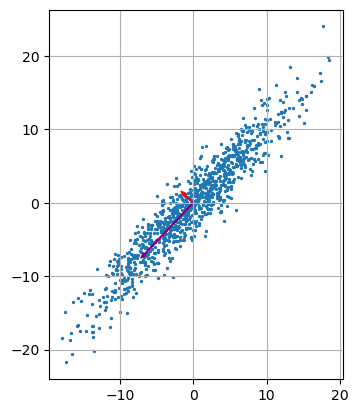
最后在二维下看一个例子，尝试修改不同的transform变量，会发现表示特征向量的箭头总是指向数据最分散或最集中的方向，且长的向量总是指向数据分散的方向，短的向量总是指向数据集中的方向。

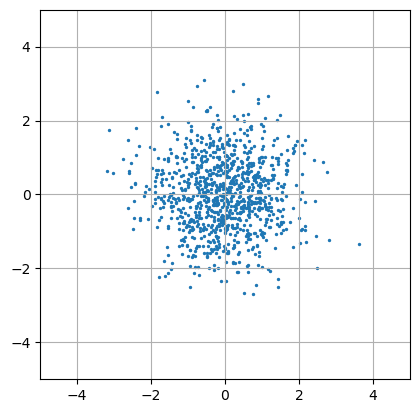
import numpy as np
import matplotlib.pyplot as plt

# 生成白噪声
x_white = np.random.normal(0, 1.0, 1000)
y_white = np.random.normal(0, 1.0, 1000)
plt.scatter(x_white, y_white, 2)

plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.grid()
plt.gca().set_aspect('equal')
plt.show()

png

def linear_transform(T, x_, y_):
    x = T[0, 0] * x_ + T[0, 1] * y_
    y = T[1, 0] * x_ + T[1, 1] * y_
    return x, y

# 对白噪声进行线性变换得到一般的二维高斯分布
transform = np.array([[6, 3], [7, 1]])
x, y = linear_transform(transform, x_white, y_white)
plt.scatter(x, y, 2)
# 画新协方差矩阵transform * transform^T的特征向量
eig, eig_vecs = np.linalg.eig(np.matmul(transform, transform.T))
plt.arrow(0, 0, eig_vecs[0, 0] * np.sqrt(eig[0]), eig_vecs[1, 0] * np.sqrt(eig[0]), width=0.1, head_width=0.5, color='red')
plt.arrow(0, 0, eig_vecs[0, 1] * np.sqrt(eig[1]), eig_vecs[1, 1] * np.sqrt(eig[1]), width=0.1, head_width=0.5, color='purple')

plt.grid()
plt.gca().set_aspect('equal')
plt.show()

png

意义2：误差椭圆长短轴的方向与大小

多元高斯分布的概率密度函数的等高线才是误差椭圆（error ellipse / uncertainty ellipse）。

先以二维为例，高维应该可以推而广之。观察多为高斯分布的定义式，等高线应该满足：

\[(\boldsymbol x-\boldsymbol \mu)^T\Sigma^{-1}(\boldsymbol x -\boldsymbol \mu) = Const \]

为了方便起见，不如就取\(Const = 1\)，且设\(\boldsymbol z = \boldsymbol x - \boldsymbol \mu\)。另外，设协方差矩阵可以相似对角化到\(\Sigma=U\Lambda U^{-1}\)，其中\(U\)是正交矩阵，则协方差矩阵的逆矩阵为\(\Sigma^{-1}=U\Lambda^{-1}U^{-1}=U\Lambda^{-1}U^T\)。于是上式化简为：

\[\begin{aligned} \boldsymbol z^TU\Lambda^{-1}U^T\boldsymbol z &= 1\\ \boldsymbol z^T\begin{bmatrix}\boldsymbol u_1& \boldsymbol u_2\end{bmatrix} \begin{bmatrix}\lambda_1^{-1}&\\&\lambda_2^{-1}\end{bmatrix}\begin{bmatrix}\boldsymbol u_1^T\\\boldsymbol u_2^T\end{bmatrix} \boldsymbol z &= 1\\ \left(\frac{\boldsymbol u_1^T\boldsymbol x}{\sqrt{\lambda_1}}\right)^2 + \left(\frac{\boldsymbol u_2^T\boldsymbol x}{\sqrt{\lambda_2}}\right)^2 = 1 \end{aligned} \]

因为\(\boldsymbol u_1\)与\(\boldsymbol u_2\)是相互垂直的单位向量（正交矩阵的性质），所以\(\boldsymbol u_1^T\boldsymbol x\)和\(\boldsymbol u_2^T\boldsymbol x\)就是向量\(\boldsymbol x\)在这两个特征向量方向上的投影，也即\(\begin{bmatrix}\boldsymbol u_1^T\\\boldsymbol u_2^T\end{bmatrix}\boldsymbol z\)是以这两个特征向量为新的基对\(\boldsymbol x\)做了一次线性变换。在这一组新的基下，椭圆方程即是标准的\(x^2/a^2+y^2/b^2=1\)的形式，因此也可以看出长短轴就是\(\sqrt{\lambda_1}\)和\(\sqrt{\lambda_2}\)，长短轴的方向就是特征向量的方向。