自控理论 第7章 频率响应补偿法

和基于根轨迹的补偿法一样，这一章的补偿法学得也非常非常浅。

7.1 超前补偿

7.1.1 超前补偿器的特性

超前补偿器的传函

\[G_c(s)=K_c\alpha\frac{Ts+1}{\alpha Ts+1}=K_c\alpha \tilde G_c(s),\ 0<\alpha<1 \]

称之为超前是因为其频率响应的相角始终大于0

\[\angle G_c(j\omega)=\angle \tilde G_c(j\omega)=\angle\frac{jT\omega+1}{j\alpha T\omega+1}=\arctan{(T\omega)}-\arctan{(\alpha T\omega)} \]

作出奈奎斯特曲线来进一步研究其特性，先求其实部和虚部

\[\tilde{G}_{\mathrm{c}}(j \omega) = \underbrace{\frac{1+\alpha(\omega T)^{2}}{1+(\alpha \omega T)^{2}}}_{\triangleq{x(\omega)}} + j \underbrace{\frac{(1-\alpha) \omega T}{1+(\alpha \omega T)^{2}}}_{\triangleq y(\omega)} \]

发现曲线刚好是个圆，因为

\[\left[x(\omega)-\frac{1+\alpha}{2\alpha}\right]^2+y^2(\omega)=\left(\frac{1-\alpha}{2\alpha}\right)^2 \]

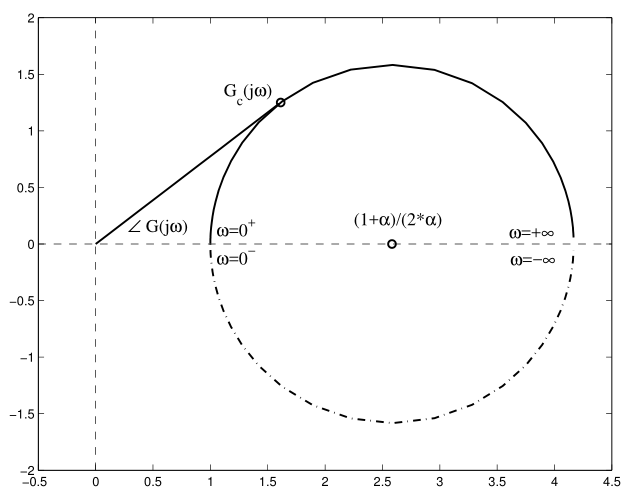
从奈奎斯特曲线中很容易看出补偿器能补偿的相位有一个最大值，对\(\angle \tilde G(j\omega)\)求导可以得到在\(\omega=\omega_m=\frac{1}{\sqrt\alpha T}\)时取得最大相位

\[\theta_m\triangleq\angle\tilde G_c(j\omega_m)=\arcsin\frac{1-\alpha}{1+\alpha} \]

其伯德图如下

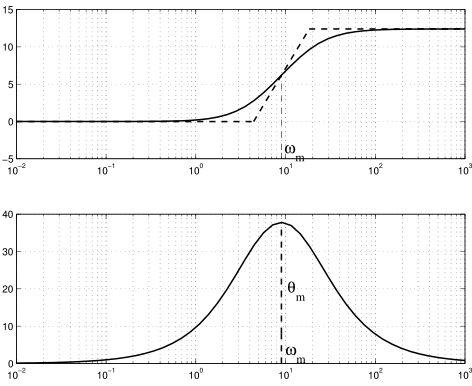
使相角取到最大的\(\omega_m\)刚好再两个转折频率的正中间。

7.1.2 通过伯德图设计超前补偿器

• 原理：超前补偿器可以增加相位 ==> 增大相位裕度 ==> 增大幅值交越频率 ==> 增大截止频率、增大带宽 ==> 改善暂态响应、改善稳定性
  • 和根轨迹补偿法的解释的出发点不一样，但结果都是一样的

1. 根据要求确定增益\(K\alpha\)
2. 由原来的相位裕度确定需要补偿的相角，也即确定超前补偿器的\(\theta_m\)
   • 一般还会流出\(5^\circ\)的富余
3. 由\(\theta_m\)计算\(\alpha\)
4. 由\(\alpha\)计算补偿器相位取得\(\theta_m\)时对应的增益，在原伯德图上找到与该增益相反的点对应的频率，取该频率为\(\omega_m\)
5. 由\(\omega_m\)计算\(T\)，得到完整的补偿器
6. 验证要求是否满足，不满足则改变\(\theta_m\)重新进行2~6步。

7.2 滞后补偿

7.2.1 滞后补偿器的特性

只要把7.1.1的\(\alpha\)换成\(\beta\)就可以得到，不过因为\(\beta>1\)而在有些地方刚好反了以下。

滞后补偿器的传函

\[G_c(s)=K_c\beta\frac{Ts+1}{\beta Ts+1}=K_c\beta \tilde G_c(s),\ \beta>1 \]

称之为超前是因为其频率响应的相角始终大于0

\[\angle G_c(j\omega)=\angle \tilde G_c(j\omega)=\angle\frac{jT\omega+1}{j\beta T\omega+1}=\arctan{(T\omega)}-\arctan{(\beta T\omega)} \]

作出奈奎斯特曲线来进一步研究其特性，先求其实部和虚部

\[\tilde{G}_{\mathrm{c}}(j \omega) = \underbrace{\frac{1+\beta(\omega T)^{2}}{1+(\beta \omega T)^{2}}}_{\triangleq{x(\omega)}} + j \underbrace{\frac{(1-\beta) \omega T}{1+(\beta \omega T)^{2}}}_{\triangleq y(\omega)} \]

发现曲线刚好是个圆，因为

\[\left[x(\omega)-\frac{1+\beta}{2\beta}\right]^2+y^2(\omega)=\left(\frac{1-\beta}{2\beta}\right)^2 \]

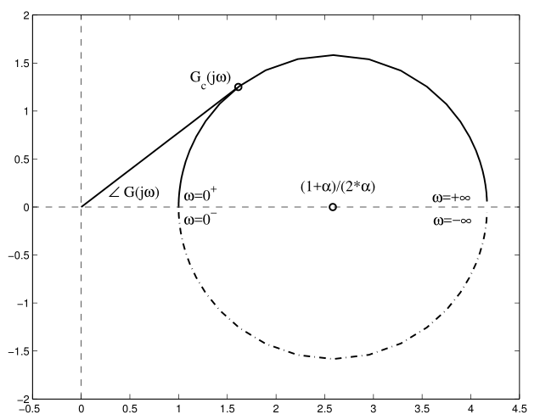
从奈奎斯特曲线中很容易看出补偿器能补偿的相位有一个最大值，对\(\angle \tilde G(j\omega)\)求导可以得到在\(\omega=\omega_m=\frac{1}{\sqrt\beta T}\)时取得最大相位

\[\theta_m\triangleq\angle\tilde G_c(j\omega_m)=\arcsin\frac{1-\beta}{1+\beta} \]

其伯德图如下

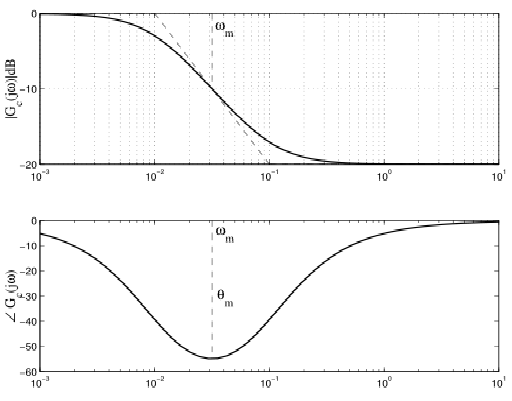
有\(\lim\limits_{\omega \rightarrow \infty}20\log\left|\tilde{G}_{\mathrm{c}}(j \omega)\right|=20\log\frac{1}{\beta}\)，也即是说滞后补偿器最多可以下压幅值响应\(20\log\frac{1}{\beta}\)

7.2.2 通过伯德图设计滞后补偿器

• 原理：滞后补偿器有明显的低通特性，会把高频的幅值响应向下压，也等效于向左移 ==> 减小幅值交越频率 ==> 减小截止频率、降低带宽，但同时增加相位裕度和幅值裕度
  • 滞后补偿会带来一个单峰的负相位，如果这个负相位处于幅值交越频率附近，则会减小相位裕度，不利于系统的稳定性，所以设计时一般都让这个负相位在负值较大时就出现，即取\(\frac{1}{T}\)和\(\frac{1}{\beta T}\)都为较小的值

1. 根据要求确定增益\(K\beta\)
2. 由原来的相位确定新的幅值交越频率\(\omega_m\)的位置
3. 由\(\omega_m\)对应的幅值确定\(\beta\)
4. 根据经验估算\(T\)，得到完整的补偿器
   • 例题中取的\(T=\frac{5}{\omega_m}\)
5. 验证要求是否满足

7.3 PID控制

只算是提了一下吧

• 微分控制器的实现

  纯粹的微分控制器会放大高频噪声，不好，一般用这个在低频上像一个微分控制器的、高频上像一个跟随器的：\(\frac{1}{1+\frac{1}{Ts}}\)

• PID参数的整定

  介绍了齐格勒-尼科尔斯方法，该方法可以借助开环系统的阶跃或者频率响应，为参数整定选取一个较为合理的初值。