自控理论 第6章 II 相对稳定性、伯德图和闭环频率响应

6.4 相对稳定性分析

前边的讨论大多局限于稳定或不稳定，现在讨论如果稳定，能有多稳定。这在实际中是很需要的，毕竟实际中充满了干扰。

6.4.1 使用保角变换分析相对稳定性

等我之后复习（预习）一下复变函数再过来补这一节吧。。。

6.4.2 \(\mathcal H_\infty\)控制

健壮（robust）控制（实在不想用“鲁棒”这种莫名其妙的翻译💢）相关，不会先留着。。。

6.4.3 幅值裕度和相位裕度

定义

• 幅值裕度

  定义相位交越频率\(\omega_1\in(0,\infty)\)，其满足\(\angle G_o(j\omega_1)=-\pi\)，则幅值裕度为

  \[K_g=\frac{1}{|G_o(j\omega_1)|} \]

  使用分贝表示则是（用的多）

  \[K_g\mathrm{dB}=20\log K_g=-20\log |G_o(j\omega_1)| \]

  • 当讨论幅值裕度的正负时，讨论的就是用分贝表示的，容易知道，当\(|G_o(j\omega_1)|\ge1\)时，\(K_g\mathrm{dB}\le0\)，反之则\(K_g\mathrm{dB}>0\)。

  • 假如奈奎斯特曲线来回穿越实轴，也即是有多个\(\omega\)满足\(\angle G_o(j\omega)=-\pi\)，这时候幅值裕度该取哪一个点来计算？

    课上没有提但是有个题涉及到了，我自己感觉如果稳定当前系统稳定，该取\((-1,j0)\)左侧最近的点；如果不稳定，该取右侧最近的点。

• 相位裕度

  定义幅值交越频率\(\omega_2\in(0,\infty)\)，其满足\(|G(j\omega_2)|=1\)，则相位裕度为

  \[\gamma=\pi+\angle G(j\omega_2) \]

幅值裕度和相位裕度单独使用不能描述系统的相对稳定性，合在一块才可以。

最小相位系统裕度的图形意义

• 一个幅值裕度和相位裕度都很大的系统，比较稳定

  

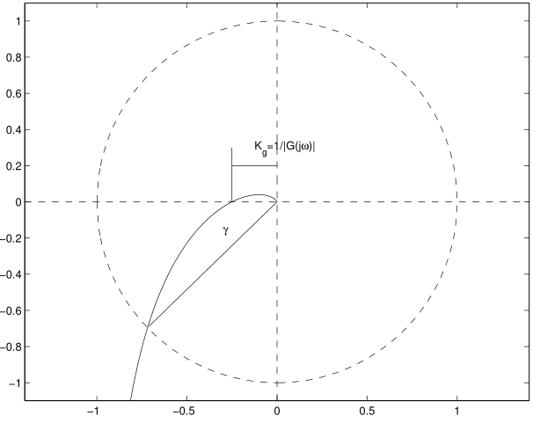
• 一个幅值裕度很大但是相位裕度很小的系统，对相角的扰动很可能使系统不稳定

  

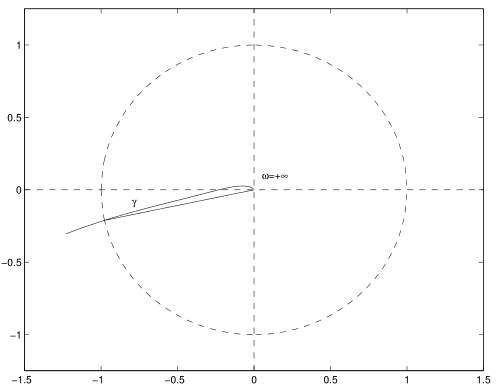
• 一个幅值裕度很小但是相位裕度很大的系统，对幅值的扰动很可能使系统不稳定

  

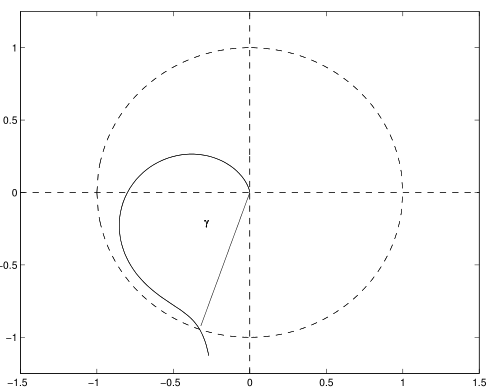
上述几幅图说明，对于最小相位系统，只有幅值裕度和相位裕度都大于0系统才能稳定。

• 注意，该结论只对最小相位系统成立。

6.5 伯德图

奈奎斯特图中频率没有得到定量体现，伯德图在这方面可以作为补充。

6.5.1 引入

• 使用对数的原因
  • 横坐标\(\omega\)：系统需要考虑的频率很宽有可能从及赫兹（机械结构）到几兆赫兹（电子系统）
  • 纵坐标\(|G(j\omega)|\)：系统经常需要作出修正，对数将乘法化为加法看起来更直观。
• 定义：对数化的频率响应曲线即是伯德图
  • 振幅响应两个轴都取对数
  • 幅角相应只有横轴取对数

6.5.2 常用环节的伯德图

常数环节

表达式如下

\[G(j\omega)=K_m\\ \Rightarrow \left\{ \begin{aligned} 20\log\left|G(j\omega)\right|&=20\log K_m\\ \angle G(j\omega)&=0 \end{aligned} \right. \]

微/积分环节

表达式如下

\[G(j\omega)=(j\omega)^{\pm1}\\ \Rightarrow \left\{ \begin{aligned} 20\log\left|G(j\omega)\right|&=\pm20\log\omega\\ \angle G(j\omega)&=\pm \frac{\pi}{2} \end{aligned} \right.\\ \]

一阶微分/惯性环节

• 表达式

  \[G(j\omega)=(1+j\omega T)^{\pm1}\\ \Rightarrow \left\{ \begin{aligned} 20\log\left|G(j\omega)\right|&=\pm20\log\sqrt{1+(\omega T)^2}\\ \angle G(j\omega)&=\pm\arctan(\omega T) \end{aligned} \right.\\ \]

• 渐近线

  可以通过\(\omega T\)与\(1\)的大小关系作伯德图的渐近线，以\(\frac{1}{1+j\omega T}\)为例（下边的讨论也是一样，毕竟一阶惯性环节见得多）：

  \[-20\log\sqrt{1+(\omega T)^2}\mathrm{dB}\approx \mathrm{Asym(\left|G(j\omega\right|)}= \left\{ \begin{aligned} &0\ & for\ \omega T\ll 1\\ &-20\log\omega T\ & for\ \omega T\gg1 \end{aligned} \right. \]

  \(\mathrm{Asym}\)指渐近线asymptote。

  

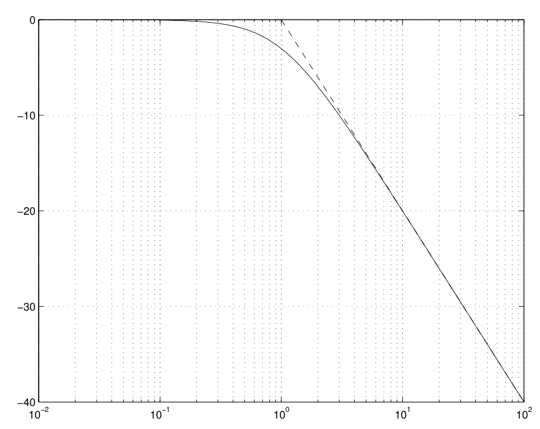
  横轴是\(\omega T\)。

  • 渐近线的误差

    渐近线与完整的幅值响应之间的误差由上图很明显在中间（\(\omega=1\)）时最大，在两头则很小，可以具体计算一下：

    \[\begin{aligned} \mathrm{Err}(\omega)&=20 \log |G(j \omega)|-\operatorname{Asym}(|G(j \omega)|) \\ &= \begin{cases}-20 \log \sqrt{1+(\omega T)^{2}} & 0<\omega T<1, \\ -20 \log \sqrt{1+(\omega T)^{-2}} & \frac{1}{T} \leq \omega T<\infty .\end{cases} \end{aligned} \]

    误差最大出现在\(\omega T=1\)处，此时\(\mathrm{Err}(\omega)\approx -3.01\)，所以\(-3dB\)是一个在手绘伯德图中经常会见到的数。

    后边还会遇到一个\(3\mathrm{dB}\)，不过出发点不一样。

• 相位

  虽然取了对数，但是相位仍然是关于\((1,\frac{\pi}{4})\)对称的，原因主要在于\(\arctan(\omega T)+\arctan{\frac{1}{\omega T}}=-\frac{\pi}{2}\)

  需要熟悉几个点：

  \[\angle\frac{1}{1+j\omega T} \left\{ \begin{aligned} &\approx 0\ &\omega T\ll 1\\ &= -\frac{\pi}{4}\ &\omega T=1\\ &\approx -\frac{\pi}{2}\ &\omega T\gg 1\\ \end{aligned} \right. \]

二阶微分/振荡环节

• 表达式

  \[G(j\omega)=[(\frac{s}{\omega_n})^2+2\zeta\frac{s}{\omega_n}+1]^{\pm1}\\ \Rightarrow \left\{ \begin{aligned} 20\log\left|G(j\omega)\right|&=\pm20\log\sqrt{\left[1-(\frac{\omega}{\omega_n})^2\right]^2+\left(2\zeta\frac{\omega}{\omega_n}\right)^2}\\ \angle G(j\omega)&=\pm\arctan{\frac{2\zeta\frac{\omega}{\omega_n}}{1-(\frac{\omega}{\omega_n})^2}} \end{aligned} \right. \]

• 渐近线

  \[\mathrm{Asym}(|G(j\omega)|)= \left\{ \begin{aligned} &0\ &\frac{\omega}{\omega_n}<1\\ &-40\log{\frac{\omega}{\omega_n}}\ &\frac{\omega}{\omega_n}\ge1 \end{aligned} \right. \]
  • 注意到\((1+s/\omega_n)^{\pm2}\)的伯德图的渐近线、相角的特殊点与二阶微分/振荡环节的完全相同，这说明一个标准二阶系统\(\frac{1}{(\frac{s}{\omega_n})^2+2\zeta\frac{s}{\omega_n}+1}\)可以用\(\frac{1}{(1+s/\omega_n)^2}\)近似。
  • 一阶环节渐近线误差只与\(\omega T\)有关，而二阶环节渐近线的误差不仅和\(\omega/\omega_n\)有关，还受\(\zeta\)控制，具体可以看下边的图。

• 相位

  这里相位响应仍然关于某点对称，虽然不是很直观，但推导思路很简单，就是取对称点带进去算，就不记笔记啦。

  需要熟悉几个点：

  \[\angle\frac{1}{(\frac{s}{\omega_n})^2+2\zeta\frac{s}{\omega_n}+1} \left\{ \begin{aligned} &\approx 0\ &\omega\ll\omega_n\\ &= -\frac{\pi}{2}\ &\omega=\omega_n\\ &\approx -\pi\ &\omega\gg\omega_n\\ \end{aligned} \right. \]

• 共振

  关于不同\(\zeta\)的伯德图如下：

  

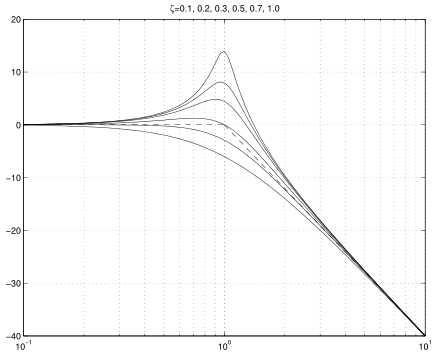
  此处的横坐标是\(\omega/\omega_n\)。

  当\(\zeta\)处于一定范围时，振幅响应会先增加后减小，其中能使幅值取到极大值的频率就称为共振频率，记为\(\omega_r\)（r指共振resonance），通过对振幅响应求导数等于0可以得到

  \[\omega_r=\sqrt{1-2\zeta^2}\omega\\ |G(j\omega_r)|=\frac{1}{2\zeta\sqrt{1-\zeta^2}} \]

  由此还可以知道只有当\(\zeta<\frac{\sqrt2}{2}\)时才会有共振现象。

6.5.3 0、1、2型系统的伯德图

不同型次系统的伯德图的不同之处仅存在于开始时的一段，设型次为\(l\)，则开始时的渐近线为

\[\mathrm{Asym}\left[G(j\omega)\right]=20\log\frac{K_o}{\omega^l} \]

• 如果延长开始时的渐近线与横轴交于\(\omega_c\)，则可以在伯德图上得到\(K_o=\omega_c^l\)
• 0型系统的伯德图：开始时是水平的
• 1型系统的伯德图：开始时是-20dB/10倍频
• 2型系统的伯德图：开始时是-40dB/10倍频

往后则都是来一个极点则-20dB/10倍频，来一个零点则+20dB/10倍频。

有了这些特征，如果又能确定所有的转折频率，则闭环传递函数可以通过伯德图直接确定下来。

---

绘制伯德图的一般步骤

1. 将传递函数写成典型环节之积
2. 找出各环节的转角频率
3. 画出各环节的渐近线
4. 如果需要在转角频率处修正渐近线得各环节曲线
5. 将各环节曲线相加

6.6.4 最小相位系统和非最小相位系统

前边提到过最小相位系统就是极点全部在闭左半平面中的系统，这是一种表述，但是没能解释它为啥叫这名儿。这里可以介绍另一种表述：最小相位系统相比具有相同幅值的其它系统，其相角的变化范围最小。

6.5.5 从伯德图确定幅值裕度和相位裕度

举个例子就会啦：

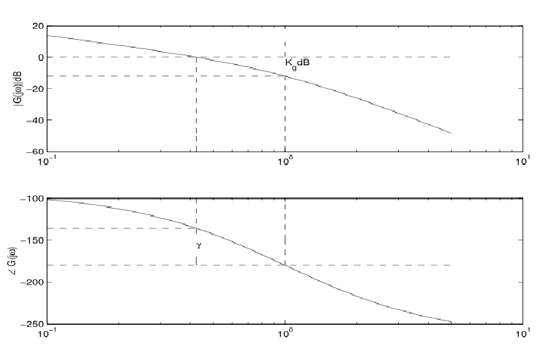
• 从相频特性中找相位交越频率，对应到幅频特性中确定幅值裕度。
  • 向下为正，上图中的幅值裕度即为正。
• 从幅值特性中找幅值交越频率，对应到相频特性中确定相位裕度。
  • 向上为正，上图中的相位裕度即为正。

6.5.6 伯德图和奈奎斯特曲线的关系

对应关系：

• 奈奎斯特曲线上单位圆对应于\(G_o(s)\)（注意不是\(G(s)\)）伯德图上的零分贝线。
• 奈奎斯特曲线上的负实轴对应于\(G_o(s)\)伯德图的\(-180^\circ\)相位线

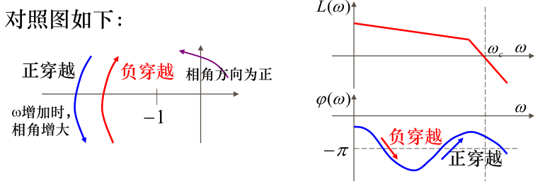
故在伯德图上可以获得奈奎斯特曲线的\(N\)，进而判断系统是否稳定。

• 注意相频曲线的穿越要发生在幅频曲线在横轴之上时，也即对应到奈奎斯特曲线\((-1,j0)\)点的左侧。

6.6 闭环频率响应

6.4、6.5两小节大部分时候（除了对比伯德图和奈奎斯特图的部分）讨论的都是不带反馈的系统，现讨论的才是带反馈系统的频率响应。

6.6.1 单位反馈系统的闭环频率响应

作出奈奎斯特图如下，则闭环传递函数的分子\(G_o(j\omega)\)和分母\(G_o(j\omega)+1\)都在其中，分别是\(\tilde{OA}\)和\(\tilde{PA}\)：

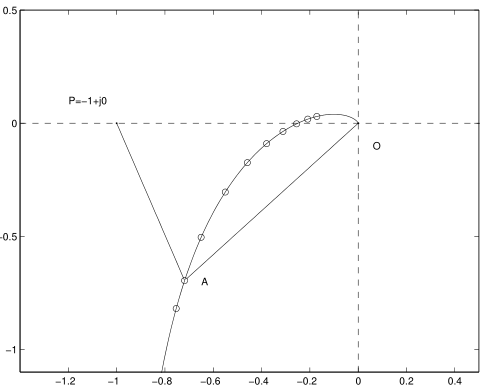
• 将\(\tilde{OA}\)和\(\tilde{PA}\)的幅值相比即可得到闭环幅值响应
• 将\(\tilde{OA}\)和\(\tilde{PA}\)的相位相减即可得到闭环相位响应

6.6.2 频率响应和暂态阶跃响应的关系

对大多数开环传函都有低通的特性，也即是

\[\begin{aligned} &\lim_{\omega \rightarrow 0}|G(j \omega)| \rightarrow \infty \\ &\lim_{\omega \rightarrow \infty}|G(j \omega)| \rightarrow 0 \end{aligned} \]

于是对于闭环传函就有

\[\lim _{\omega \rightarrow 0} \frac{|G(j \omega)|}{|1+G(j \omega)|}=1, \quad \lim _{\omega \rightarrow \infty} \frac{|G(j \omega)|}{|1+G(j \omega)|}=0 \]

所以一般会有一个频率能够使得闭环幅值增益为\(1/\sqrt 2\)。当增益小于\(\frac{1}{\sqrt 2}\)时，我们认为增益太小，对输出影响太小，就说到此处截止了，对应的频率即是截止频率\(\omega_b\)。化到分贝数是

\[20\log\frac{1}{\sqrt 2}\approx-3\mathrm{dB} \]

• 在从0到截止频率的这一段频带上，各次谐波增益都较大，可以认为属于这些频率的输入是通过系统得到输出了的，这一段频带的长度就称为带宽。
  • 带宽越宽，对高频输入的增益就越大，系统响应也就越快（对应上升时间越短），但同时噪音也会增加，这两者有时需要做取舍。
• 截止频率处幅频特性曲线地斜率称为衰减斜率。
  • 这个斜率越大，之前所说的“截至”的概念就越准确。但是往往需要做出取舍，因为对于二阶系统来说，越大的衰减斜率就意味着谐振时的增益也越大，对稳定性有损害。

6.6.3 等幅值轨迹和等相位轨迹

本节关心\(G_o(j\omega)\)平面上哪些点能使闭环传函的幅值或相位为某一定值。为了分析讨论，现把\(G_o(j\omega)\)拆成虚实两部分：\(G_o(j\omega)=x+jy\)。

本节没有深入了解，需要时再回来咯

等幅值轨迹（M圆）

\[\begin{aligned} \left|\frac{G_o(j \omega)}{1+G_o(j \omega)}\right|=M & \Longleftrightarrow\left|\frac{x+j y}{1+x+j y}\right|=M \\ & \Longleftrightarrow \frac{x^{2}+y^{2}}{(1+x)^{2}+y^{2}}=M^{2}\\ & \Longleftrightarrow \left(x+\frac{M^2}{M^2-1}\right)^2+y^2=\left(\frac{M^2}{1-M^2}\right)^2 \end{aligned} \]

是个圆心在实轴上的圆！

等幅位轨迹（N圆）

看看在\(\angle G_o(j\omega)=N=Const\)时轨迹如何：

由图知\(\alpha_1-\alpha_2=\alpha\)，即

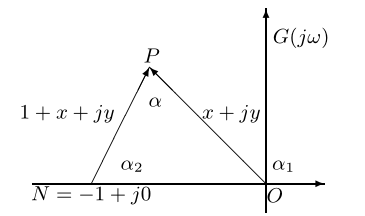
\[\begin{aligned} \arctan\frac{y}{x}-\arctan\frac{y}{1+x}&=\angle\frac{x+jy}{1+x+jy}\\ \tan{\left(\arctan\frac{y}{x}-\arctan\frac{y}{1+x}\right)}&=\tan{\left(\angle\frac{x+jy}{1+x+jy}\right)}\\ \frac{\frac{y}{x}-\frac{y}{1+x}}{1+\frac{y^2}{x(1+x)}}&=\frac{y}{x^2+x+y^2}\\ \Rightarrow\left(x+\frac{1}{2}\right)^2+\left(y-\frac{1}{2N}\right)^2&=\frac{1}{4}+\left(\frac{1}{2N}\right)^2 \end{aligned} \]

还是个圆（其实是个弧，下半平面没有）！