自控理论 第04章 根轨迹方法

4.1 引入

• 劳斯判据的缺陷

  虽然能判断是否稳定，但是不能判断稳定后的各项指标如何，具体来说就是劳斯判据不能反映超调量、上升时间等信息。所以还要继续找新的方法，本章介绍的根轨迹方法就是一种既能判稳，又能反应稳定后的其他指标的方法。

• 定义

  • 开环传递函数

    不失一般性地，令前向支路传递函数$G(s)=\frac{N_1(s)}{D_1(s)}$与反馈支路传递函数$H(s)=\frac{N_2(s)}{D_2(s)}$，则它们的乘积定义为开环传递函数（return ratio）$G_o(s)$。

    

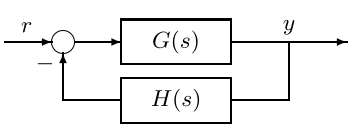    $$G_o(s)=G(s)H(s)=\frac{N_1(s)}{D_1(s)}\cdot\frac{N_2(s)}{D_2(s)}=\frac{K(s-z_1)(s-z_2)\cdots(s-z_m)}{(s-p_1)(s-p_2)\cdots(s-p_n)}=\frac{KN_o(s)}{D_o(s)}$$

    • 此处的开环传递函数和上一章的开环传递函数其实是同一个东西，只不过上一章中都是单位反馈$H(s)=1$，所以就有$G_o(s)=G(s)H(s)=G(s)$了。
    • 以上述的形式表示开环传递函数，则$K$称为根轨迹增益。

  • 特征方程

    $$D(s)=N_1(s)N_2(s)+D_1(s)D_2(s)=D_o(s)+KN_o(s)$$

4.3 构建根轨迹的规则

与其说是规则不如说是规律，不过ppt上用的rule，老师也说的规则，就按规则来吧。。

根轨迹的定义

随着$K$从0增大到$\infty$，特征方程$D_o(s)+KN_o(s)=0$的根，也即原闭环传递函数的极点在复平面上的运动轨迹称为根轨迹。为了方便后边的分析，一般还都写为下列定义式中$\frac{N_{\mathrm{o}}(s)}{D_{\mathrm{o}}(s)}=-\frac{1}{K}$的形式

$$\mathcal{R} \mathcal{L}\left(D_{\mathrm{o}}, N_{\mathrm{o}}\right)=\left\{s: \frac{N_{\mathrm{o}}(s)}{D_{\mathrm{o}}(s)}=-\frac{1}{K}, K \in[0, \infty)\right\}$$

注意：虽然下边一直在拿$G_o(s)$讨论，但根轨迹不是$G_o(s)$极点的轨迹，而是原来的闭环传递函数极点的轨迹。

• 相角条件：由定义有$G_o(s)=-1\quad s\in\mathcal{RL}(D_o,N_o)$，故根轨迹上的点满足

  $$\angle G_o(s)=(2k+1)\pi,s\in\mathcal{RL}(D_o,N_o)$$

• 幅值条件：由定义易知

  $$K=\left|\frac{D_o(s)}{N_o(s)}\right|$$

规则0：实系统的根轨迹总是关于实轴对称

因为复数根总是共轭的，所以它们的轨迹也会关于是轴对称。

规则1：根轨迹分支的个数等于开环传递函数$G_o(s)$的阶次

这里假设$D_o(s)$和$N_o(s)$已经没有公因式了。则根据$n$此方程有$n$个根的定理，易得此规则。

规则2：根轨迹起点和终点的规律

$K\to0$时，$G_o(s)=\frac{N_o(s)}{D_o(s)}\to\infty$，故根轨迹起始于开环传递函数的极点；

$K\to\infty$时，$G_o(s)=\frac{N_o(s)}{D_o(s)}\to0$，故根轨迹终止于开环传递函数的零点。

• 注意无穷远也可能是零点。

规则3：实轴上根轨迹的规律

实轴上一点右边的零/级点个数（重根算多个）若为奇数，则该点在根轨迹上，反之则不在。

• 证明：

  $s$在实轴上时，有

  $$\frac{N_o(s)}{D_o(s)}=\frac{K(s-z_1)(s-z_2)\cdots(s-z_m)}{(s-p_1)(s-p_2)\cdots(s-p_n)}<0$$

  对于共轭的极点或零点$s_1,s_2$，总有$|s-s_1||s-s_2|=|s-\sigma-j\omega||s-\sigma+j\omega|=(s-\sigma)^2+\omega^2>0$，所以它们不会使得开环传函为负。继续考虑实数的零点和极点$s_0$，如果$(s-s_0)<0$，有$s<s_0$，即该点$s_0$会在这段根轨迹的右边。再稍微扩展一下就得到了该条规则。

规则4：$s\to \infty$时根轨迹渐近线的规律

推导翻书，太长不抄啦。思路：将$\frac{D_o}{N_o}$展开为$s$的多项式，省略$s\to\infty$时的二阶小量，然后再泰勒展开一次，计算稍微多一点，建议背下来咯。

$$s-\frac{\sum\limits_{j=1}^np_j-\sum\limits_{i=1}^mz_i}{n-m}\approx K^{\frac{1}{n-m}}e^{j\frac{(2k+1)\pi}{n-m}}$$

故渐近线与x轴的截距和夹角为

$$\left\{ \begin{aligned} \sigma_a&=\frac{\sum\limits_{j=1}^np_j-\sum\limits_{i=1}^mz_i}{n-m}\\ \theta_a&=\frac{(2k+1)\pi}{n-m} \end{aligned} \right.$$

规则5：分离点、汇合点的规律

• 定义

  • 分离点：实轴上相邻两极点之间的根轨迹在该点脱离实轴。
  • 汇合点：实轴上相邻两零点之间的根轨迹在该点到达实轴。

• 特点：分离点、汇合点是开环增益$K=-\frac{D_o(s)}{N_o(s)}$沿实轴变化时的极值点。举个例子，根轨迹终止于实轴上两个相邻的零点，则在两条根轨迹从汇合点出发然后终止于两零点的过程中，$K$一直增大，故汇合点处的$K$就是这两个零点之间的极小值。

  • 分离点是极大值点。
  • 汇合点是极小值点。

• 计算：此时的极点$s$满足$\frac{\mathrm d}{\mathrm d s}\frac{D_o(s)}{N_o(s)}=0$，既满足

  $$D_o'(s)N_o(s)-N_o'(s)D_o(s)=0$$
  • 要注意该方程的解只是驻点（stationary point，即一阶导数为0的店），而驻点不一定是极值点。严格来说要检查高阶导数以排除非极值点的情况，但一般遇不到。。。

规则6：根轨迹出射角、入射角的计算

由相角条件有

$$\angle G_o(s)=\sum\limits_{i=1}^m(s-z_i)-\sum\limits_{i=j}^n(s-p_j)=(2k+1)\pi$$

让$s$趋近极点和零点可以得到以下结论（非重根的结论是易得到的，至于重根为什么是除一个$n$得到的，课上没有解释）

• 出射角：下标_d指departure，即离开极点；$n_l$是指这个极点是$n_l$重极点。

  $$\theta_{d,l}=\frac{1}{n_l}\left[(2k+1)\pi+\sum\limits^m_{i}\angle(p_l-z_i)-\sum\limits^n_{j\ne l}\angle(p_l-p_j)\right]$$

• 入射角：下标_a指approach，即趋近零点；$n_h$是指这个极点是$n_h$重零点。

  $$\theta_{a,h}=\frac{1}{n_h}\left[(2k+1)\pi-\sum\limits^m_{i\ne h}\angle(z_h-z_i)+\sum\limits^n_{j}\angle(z_h-p_j)\right]$$

规则7：虚轴穿越点、临界稳定根轨迹增益的计算

假设根轨迹在$(0,j\omega)$穿越虚轴，且此时的增益为$K_{cr}$（_cr指critical，此时系统临界稳定），则满足

$$K_{cr}N_o(j\omega)+D_o(j\omega)=0$$

将$N_o(j\omega)$、$D_o(j\omega)$用$a+jb$的形式表示，则可以得到一个关于$K_{cr}$和$\omega$的方程组，解该方程组即可得到它俩。

$$\left\{ \begin{aligned} N_o(j\omega)=h_N(-\omega^2)+j\omega g_N(-\omega^2)\\ D_o(j\omega)=h_D(-\omega^2)+j\omega g_D(-\omega^2) \end{aligned} \right.\\ $$

规则8：根轨迹在实轴上的交点的规律

规则5是规则8的特例，规则5描述的是两条根轨迹在实轴上相交的规律，规则8描述的则是$r$条根轨迹在复平面上任意一点相交的规律。

假设$r$条根轨迹相交于$s_0$，则此时有（用的不多，证明翻书吧）

$$\left.\frac{\mathrm d^k}{\mathrm d s^k}\frac{D_o(s)}{N_o(s)}\right|_{s=s_0}=0,\forall 1\le k\le r-1$$

故求解上述方程，然后将解带入$\frac{D_o(s)}{N_o(s)}$验证是否为负实数即可得到根轨迹的交点。

• 同时$s_0$还是特征方程的$r$重根，由根轨迹的定义可以的到这个表述。
• 分离点和汇合点只涉及到了根轨迹在实轴上的相交，但此处得到的交点可能在复平面上的任意一点。

规则9：$n-m\ge2$时，闭环极点的和等于开环极点的和

假设开环极点为$r_i\ i\in[1,n]$，则有

$$\prod_{j=1}^{n}\left(s-p_{j}\right)+K \prod_{i=1}^{m}\left(s-z_{i}\right)=\prod_{k=1}^{n}\left(s-r_{k}\right)$$

当$n-m>2$时通过上式求$s^{n-1}$的系数即可得到该规则。

• $K$增大时，闭环极点会变化，但开环极点不会变化。该规则说明了当$n-m>2$时，虽然闭环极点会随着$K$增大而变化，但它们的总和不会变，所以如果有一条根轨迹随着$K$增大而向左走，则为了极点之和不变就一定会有一条根轨迹向右走，这条根轨迹在$K$较大时则很有可能导致系统不在稳定。

规则10：这10条规则不能唯一确定根轨迹

只是一些规律嘛，这是当然的。现在毕竟有Python有MatLab，学这个很大一部分原因应该只是应付考试中的手绘根轨迹题目了。

手绘步骤

1. 求出开环传函
2. 求出开环传函的零、极点
3. 确定实轴上的根轨迹
4. 求出分离点、汇合点
5. 求出出射角和入射角
6. 求出穿越点、临界稳定根轨迹增益
7. 求出渐近线
8. 定性手绘

4.4 特殊的根轨迹

4.4.1 其他系统参数的根轨迹（广义根轨迹）

先写出特征方程，然后把它调整成以下形式

$$\frac{N_o'(s)}{D_o'(s)}=-\frac{1}{\theta_i}$$

其中$\theta_i$是关心的系统参数，则就又可以用上一节中的方法画根轨迹啦。

4.4.2 正反馈系统的根轨迹（零度根轨迹）

形成正反馈既可能由综合点的符号导致，也可能由反馈通路传递函数$H(s)$系数的符号导致，确定到底是不是正反馈系统，稳妥的方法是看特征方程写成什么样：

$$D_o(s)\pm KN_o(s)=0$$

其中

$$\left\{ \begin{aligned} N_o(s)&=(s-z_1)(s-z_2)\cdots(s-z_m)\\ D_o(s)&={(s-p_1)(s-p_2)\cdots(s-p_n)}\\ \end{aligned} \right.$$

如果取正号则是负反馈，规则按普通的根轨迹来；反之则是零度根轨迹，所有普通根轨迹中涉及$(2k+1)\pi$的地方都得改为$2k\pi$。

• 相角条件

  $$\angle G_o(s)=2k\pi,s\in\mathcal{RL}(D_o,N_o)$$

• 规则3

  实轴上一点右边的零/级点个数（重根算多个）若为偶数，则该点在根轨迹上，反之则不在。

• 规则4

  $$s-\frac{\sum\limits_{j=1}^np_j-\sum\limits_{i=1}^mz_i}{n-m}\approx K^{\frac{1}{n-m}}e^{j\frac{2k\pi}{n-m}}$$

• 规则6

  • 出射角：下标_d指departure，即离开极点；$n_l$是指这个极点是$n_l$重极点。

    $$\theta_{d,l}=\frac{1}{n_l}\left[2k\pi+\sum\limits^m_{i}\angle(p_l-z_i)-\sum\limits^n_{j\ne l}\angle(p_l-p_j)\right]$$

  • 入射角：下标_a指approach，即趋近零点；$n_h$是指这个极点是$n_h$重零点。

    $$\theta_{a,h}=\frac{1}{n_h}\left[2k\pi-\sum\limits^m_{i\ne h}\angle(z_h-z_i)+\sum\limits^n_{j}\angle(z_h-p_j)\right]$$