自控元件 第2章 变压器
2.1 概述
-
应用
- 变交流电的压,但是不能变频。
- 可以起到电气隔离的效果。
-
结构
- 铁心:常用厚0.35~0.5mm两边涂有绝缘漆的电工钢片叠压而成。
- 线圈绕组:可能有一组或多组。
- 一般至少由两个绕组,输入边的较一次绕组,负载边的叫二次绕组。
2.2 单相变压器的空载运行
正方向约定(以及复习电分)
书上的符号和记法(我感觉)非常恶心,反正我是不想用💢
- 电分中应该有更加全面的讨论,不过我忘得差不多了。。。如果电分学得好会请无视本节内容。
- 看到后面发现,用E来表示电感两端的电压是贯穿整本教材的习惯,所以也无可厚非吧。但这使得\(E_L=-L\frac{\mathrm dI}{\mathrm dt}\)多了一个负号,配合上乱七八糟的箭头方向,反正我还是习惯不了,况且全书设计电分计算最多的也就是本章,我就按电分的习惯来啦。
复习电分并重新约定符号:
-
电压源用字母E表示,电压降用U表示
- 电感两端的电压降为\(U_L=L\frac{\mathrm dI}{\mathrm d t}\)
-
理想变压器
-
对于输入端的电路来说,变压器可能是任意一种负载(纯电阻、阻感、阻容等),这取决于输出端的电路。
- 强调这一点是因为我之前有一个错误的认识:因为变压器的原理是通过电感来推导的,所以我之前一直就以为理想变压器相当于输入端电路和数出端电路各有一个电感。但仔细一想马上就会发现问题:单个电感两端的电压和通过电感的电流相位相差90度,所以如果输入端是一个电感,它将永远无法传递有功功率。
- 错误认识的原因是我忘了还有个东西叫互感,它使得有功功率可以在两个线圈之间传输。
-
对于输出端的电路来说,变压器提供有功功率,如同一个交流电压源。
-
设输入端的变压器线圈匝数\(N_1\),承受压降\(U_1\),过电流\(I_1\);输出端的变压器线圈匝数\(N_2\),提供电动势\(E_2\),过电流\(I_2\),则满足关系
\[\frac{\tilde U_1}{\tilde E_2}=K=\frac{N_1}{N_2}\\ U_1I_1=E_2I_2 \]- 注意该式同时还说明了二次绕组的电动势与一次绕组上的压降同相位。
-
空载变压器的分析
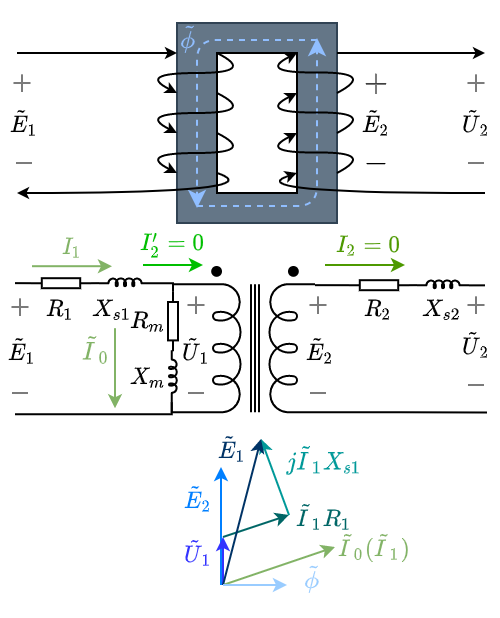
实际变压器可以等效为以下几个部分
- 理想变压器。
- \(R_m\):铁心损耗等效出来的电阻。
- \(X_m\):绕组电感。
- \(X_{si}\):漏感,下标1和2分别代表一次绕组和二次绕组的漏感。
- \(R_i\):绕组电阻,下标1和2分别代表一次绕组和二次绕组的绕组电阻。
因为此时空载,所以二次绕组断路,其中没有电流。可以作出相量图并列出方程
上图是示意图,具体的相位关系还需要根据具体负载才能确定,比如\(\tilde E_1\)的相位就不一定落后于\(\tilde E_2\)。
经过理想变压器的电流为0,那怎么会有磁通\(\tilde \phi\)的呢?
别忘了上图中的原理图说到底仍然只是一个等效模型,实际上线圈就绕在铁心上,实际变压器空载时铁心内肯定也还是有磁通的。
-
实际上因为空载电流小、绕组电阻小、漏感小,近似有
\[\tilde E_1\approx \tilde U_1 \] -
电流可以分为两部分看,其中一部分被损耗掉了,另一部分则建立了空载时的磁通。把后边这部分称为“磁化电流”(命名和大物重了,尽管表示的不是同一个东西),用\(I_{\phi0}\)表示它。
- 按照毕奥-萨法尔定律,磁化电流和磁通在时域上应该是同相位的。
2.3 单相变压器的负载运行
绕组折合
负载加上之后,直接分析需要在一次绕组、二次绕组两边的电路建立两个方程组,然后通过变压器把两个方程组联系起来求解。为了稍微简化一点点,引入绕组折合的方法,该方法可以拿掉理想变压器,让分析再次回到只有\(R\)、\(L\)、\(C\)的电路。
-
折合的目标:上图中最靠下的电路,且因为主要需分析的是各元件的功率,各带’的元件与原来的元件消耗的有功或无功功率应相同。
-
折合的方法:
首先把电流就用的\(I_2'\),变压器使得
\[I_2'=\frac{1}{K}I_2 \]故如果电阻、电感(和电容)想保持其功率,要满足
\[\left\{ \begin{aligned} \frac{1}{\sqrt2}I_2'^2R'&=\frac{1}{\sqrt{2}}I_2^2R\\ \frac{1}{\sqrt2}I_2'^2X'&=\frac{1}{\sqrt{2}}I_2^2X(无功功率)\\ \end{aligned} \right. \Rightarrow \left\{ \begin{aligned} R'&=K^2R\\ X'&=K^2X \end{aligned} \right. \]自控元件中谈容性负载的地方很少,原因大概是这门课大多时候处理的都是电机,而电机就我所知道的都算感性负载。
进一步,各个电压则满足
\[U_i'=jI_2'X_i'=j\frac{I_2}{K}\cdot K^2X_i=K\cdot jI_2X_i=KU_i \]
负载变压器的分析
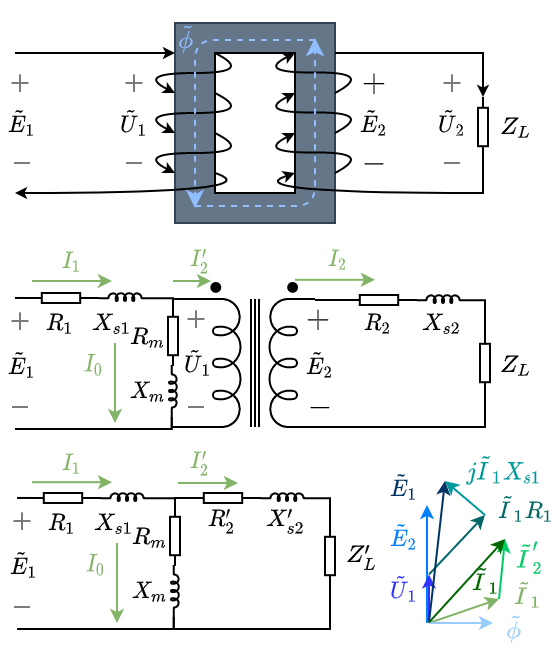
有了前边的铺垫,这个很容易直接写啦:
- 有时候还会做简化
- 绕组电阻小、漏感小,忽略它们的影响则\(R_m\)和\(X_m\)就相当于直接接到了电源\(E_1\)两端,所以可以近似认为负载和空载时流经\(R_m\)和\(X_m\)的电流\(I_0\)不变。
- 进一步,认为\(X_m\)很大,所以\(I_0\)很小,进一步\(R_m\)和\(X_m\)这个支路对其他部分的影响也很小,可以直接丢掉。
- 绕组电阻小、漏感小,忽略它们的影响则\(R_m\)和\(X_m\)就相当于直接接到了电源\(E_1\)两端,所以可以近似认为负载和空载时流经\(R_m\)和\(X_m\)的电流\(I_0\)不变。
2.3 变压器的额定值和特性
额定值
- 额定电压
- 一次额定电压\(U_{1N}\)
- 二次额定电压\(U_{2N}\):一次绕组接额定电压后,二次绕组空载时的电压
- 额定电流
- 一次额定电流\(I_{1N}\)
- 二次额定电流\(I_{2N}\)
- 额定容量:额定视在功率\(S_N=U_{1N}I_{1N}\)
- 额定频率:工业上一般为50Hz
- 电压调整率:\(\Delta U=\frac{U_{2N}-U_2}{U_{2N}}\),其中\(U_2\)为实际工作时的输出电压。
特性
ppt给了这么一张图就完事了。。。大概是要我们记结论。
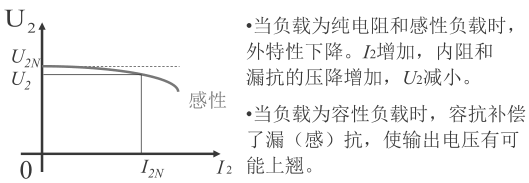
这张图叫“变压器的外特性”,其实不就是\(U_2=f(I_2)\)嘛。
现在来简单研究一下原因。首先简化一下电路,认为\(X_m\)很大,所以丢掉\(X_m\)和\(R_m\);然后\(X_2'\)和\(R_2'\)相比\(X_L'\)又很小,所以把\(X_2'\)和\(R_2'\)也丢掉,那么输出电压满足
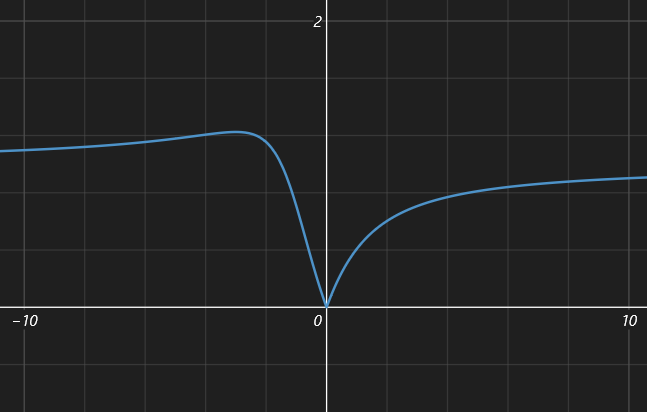
\[\begin{aligned} \tilde U_2&=\frac{jX_L'}{R_{1}+j(X_{s1}+X_L')}\tilde E_1\\ &=\left({1+\frac{R_{1}+jX_{s1}}{jX_L'}}\right)^{-1}\tilde E_1\\ \end{aligned} \Rightarrow |\tilde U_2|=\frac{|X_L'|}{\sqrt{X_L'^2+2X_s'X_L'+(X_s'^2+R_1^2)}}|\tilde E_1| \]如果负载是纯电感负载,则\(X_L>0\),反之是纯电容负载则\(X_L<0\),随便取个参数画一下上边的关系试试\(y=\frac{|x|}{\sqrt{x^2+2x+3}}\):
这说明如果负载是纯电容,随着容抗减小,电流增大,电压会先上升后下降;如果是纯电感,则随着感抗减小,电流增大,电压会一直下降。看来ppt这回应该没说错😂。如果再仔细一点,还可以讨论容性负载时来个谐振什么的(都快忘了我是在学啥了😵)
能量流动
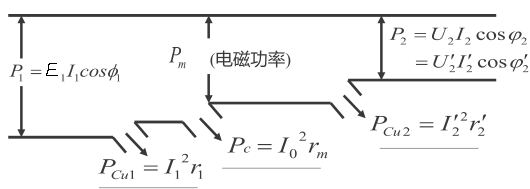
所以效率有
2.4 特殊变压器
-
自耦变压器
- 一定是一个降压变压器
- 优点:额定容量相同时,所用材料少,重量体积小,损耗低。
- 缺点:容量较小,且一、二次绕组之间有电的联系,起不到隔离的作用。
-
电压互感器
- 二次绕组接电压表,用于测量高压电。
- 从变压器的角度讲是一个降压变压器。
- 使用注意
- 绕组都应装熔断器,防止电流过大
- 二次绕组、铁心、外壳都应接地
-
电流互感器
-
二次绕组接电流表,用于测量大电流。
-
从变压器的角度讲是一个升压变压器。
-
使用注意
二次绕组不应接熔断器,二次绕组也必须避免开路。若开路
- 一次绕组中的大电流将变为空载电流(原来的大电流主要施加到负载上,因为负载经升压变压器绕组折合之后阻抗很小),导致铁心损耗大幅增加。
- 二次绕组是高压侧,开路可能会导致击穿。
-
2.5 变压器的使用
单相变压器实物有四个抽头
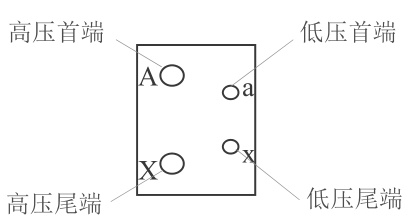
且实际做出来的变压器\(K\)不一定都是正的(此时称A与a为同名端),有的也会做成负的(此时称A与a为异名端)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号