电力电子 第1章 绪论

参考：《电力电子技术》冬雷

电感伏秒平衡和电容安秒平衡

对于理想的电感和电容，首先我们有$L\frac{{\rm d}i_L}{{\rm d}t}=u_L$和$C\frac{{\rm d}u_C}{{\rm d}t}=i_C$，现在考虑若电路达到了稳态，那么一个周期内$\Delta i_L$和$\Delta u_C$都应该是0：

$$\Delta i_L=\frac{1}{L}\int_0^Tu_L{\rm d}t=0V\cdot s\\ \Delta u_C=\frac{1}{C}\int_0^Ti_C{\rm d}t=0A\cdot s\\ $$

于是可以发现，达到稳态时，电感平均电压应该为0，电容平均电流应该为0。伏秒平衡和安秒平衡指的就是这个。

三相电路基本知识

• 星形连接

  

  $$\begin{aligned} \dot U_A、\dot U_B、\dot U_C&——相电压\\ \dot U_{AB}、\dot U_{BC}、\dot U_{CA}&——线电压\\ \dot I_{A}、\dot I_{A}、\dot I_{A}、\dot I_{AB}、\dot I_{BC}、\dot I_{CA}&——相电流/线电流 \end{aligned}$$
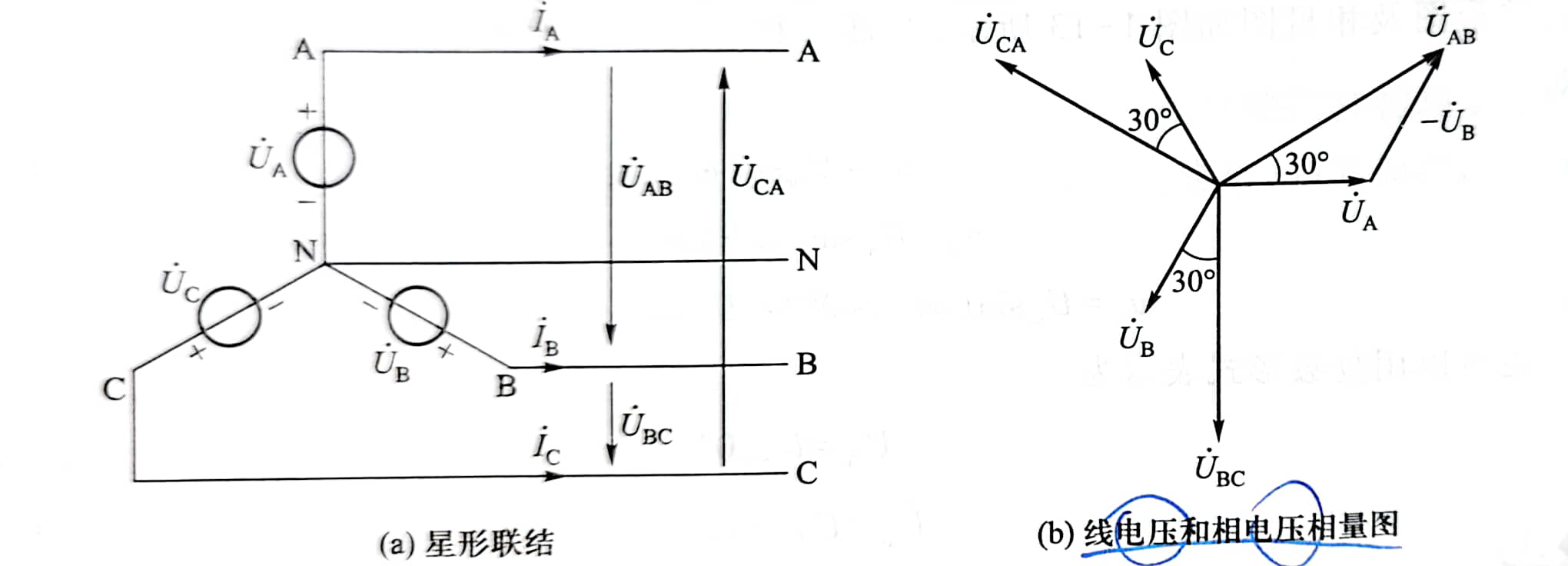
  • 当负载对称时，线电压相位超前对应相电压$30^\circ$，幅值为$\sqrt 3$倍，原因见上右图。
  • 相电流等于线电流。
  • 按是否引出零线（N），分为三相三线制和三相四线制。

• 三角形连接

  

  $$\begin{aligned} \dot U_A、\dot U_B、\dot U_C、\dot U_{AB}、\dot U_{BC}、\dot U_{CA}&——相电压/线电压\\ \dot I_{AB}、\dot I_{BC}、\dot I_{CA}&——相电流\\ \dot I_{A}、\dot I_{A}、\dot I_{A}&——线电流 \end{aligned}$$

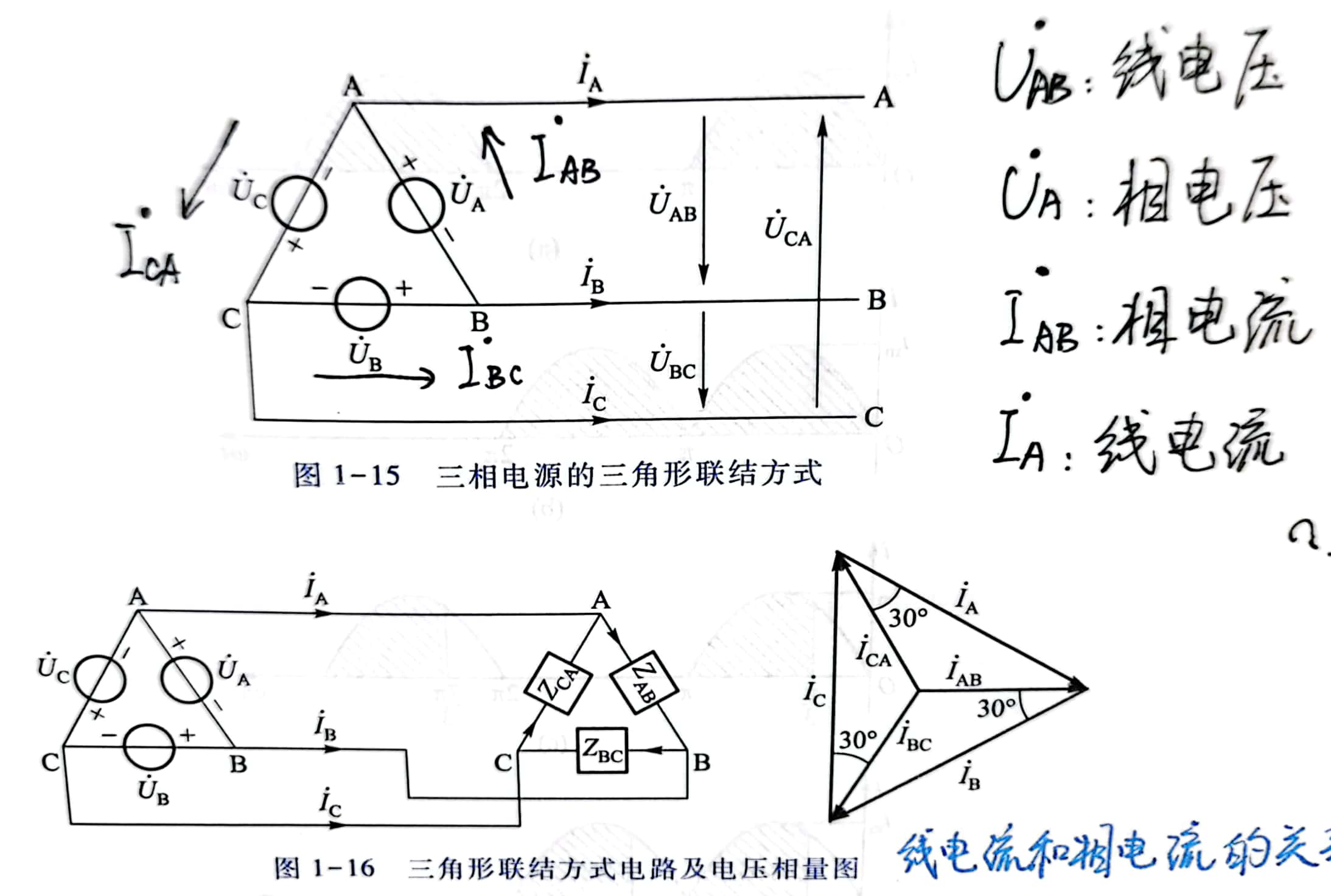
  各个变量的名字让我纠结了蛮久，但从含义上来总结：

  • 相电压：三相中的一相电源的电压
  • 线电压：三相输出的两根线之间的压差
  • 相电流：流过三相中的一相电源的电流
  • 线电流：三相输出的一根线上流过的电流

  • 线电压等于相电压。
  • 当负载对称时，线电流落后对应相电流$30^\circ$，幅值为$\sqrt{3}$倍。

• 功率

  用下标$p$表示“相”上的量，用下标$l$表示线上的量。对比两种接法，发现它们都满足

  $$P=3U_pI_p=\sqrt 3U_lI_l$$

描述非正弦波

• 非正弦波形的有效值：设其平均值为$A_0$，其$i$次谐波的幅值为$A_i$，由有效值的定义有

  $$A_{rms}=\sqrt{A_0^2+\frac{1}{2}\sum\limits_{i=1}^nA_i^2}$$

• 总畸变率：谐波的平方和与基波之比

  $$THD=\frac{\sqrt{\sum\limits_{i=2}^\infty A_i^2}}{A_1}$$

• 非正弦电路的功率因数

  • 研究对象：电压为正弦，电流为非正弦的情形。

  • 定义：做傅里叶分解，基波电流为$I_1$，与电压的相位差为$\varphi_1$，则有功功率定义为$P=UI_1\cos\varphi_1$，功率因数定义为基波因数$\nu$和位移因数$\cos\varphi_1$的乘积

    $$\lambda=\frac{UI_1\cos\varphi_1}{UI}=\frac{I_1}{I}\cos\varphi_1=\nu\cos\varphi_1$$

    其中$\nu=\frac{I_1}{I}$称为基波因数。