2.1 系统的三种代数表示方法
2.1.1 微分方程表示
没有大物和电分之外的新东西🤷♂️
2.1.2 传递函数表示
- 直接对输入输出做拉普拉斯变换然后相除即可得到传递函数。
- 系统的单位冲激响应的拉普拉斯变换即是系统的传递函数。
2.1.3 状态空间表示
通过设置合适的变量,可以将高阶微分方程(组)改写为一阶微分方程组,再以向量的形式表示就得到了该系统的SSR:
{˙x(t)=Ax(t)+bu(t)y(t)=cTx(t)+du(t)
还可以写向量化更彻底的形式:
[˙xy]=[AbcTd][xu]
特点
- 一阶常系数线性微分方程组
- A是一个方阵
- 相比单一的高阶微分方程,状态空间表示包含了更多关于系统的信息,并在一定程度上展现了系统的内部结构。
非线性系统的线性化
向量导数的定义:
∂f∂t≜⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣∂f1∂t∂f2∂t⋮∂fn∂t⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦∂g∂xT≜[∂g∂x1∂g∂x2…∂g∂xn]∂f∂xT≜⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣∂f1∂xT∂f2∂xT⋮∂fn∂xT⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦=⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣∂f1∂x1∂f1∂x2…∂f1∂xn∂f2∂x1∂f2∂x2…∂f2∂xn⋮⋮⋱⋮∂fn∂x1∂fn∂x2…∂fn∂xn⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦
-
非线性系统的状态空间表示一般可以写为:左边仍是状态变量的一阶导数,右边是关于状态变量和输入的非线性函数。
{˙x=f(x,u)y=g(x,u)
-
平衡点
当输入u(t)=u0时,˙x=∂x∂t=0,此时的x处于平衡态。
-
线性化
-
思想:在平衡点附近,用一阶近似代替非线性函数
-
计算
令˙xδ=˙x−˙x0,uδ=u−u0,则
[˙xδyδ]=[AbcTd][xδuδ]
其中
[AbcTd]=⎡⎢
⎢
⎢⎣∂f∂xT∣∣x=x0u=u0∂f∂u∣∣x=x0u=u0∂g∂xT∣∣x=x0u=u0∂g∂u∣∣x=x0u=u0⎤⎥
⎥
⎥⎦
2.2 三种代数表示法的相互转换
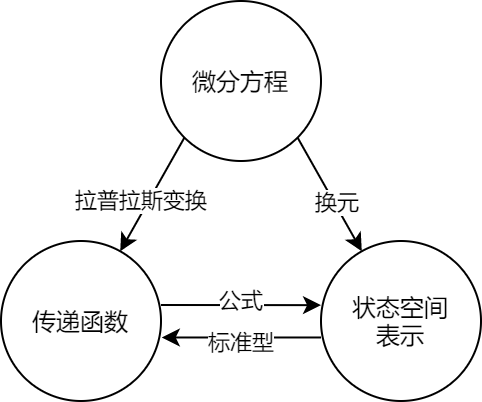
从传递函数到微分方程和从状态空间到微分方程没有详细展开,前者只是做拉普拉斯逆变换,后者只是做方程组消元。
2.2.1 从微分方程到传递函数
回忆信号与系统。特别要注意一个前提:假设所有的初态都是0。
2.2.2 从微分方程到状态空间表示
前边已经说过啦。
2.2.3 从状态空间表示到传递函数(单入单出系统)
对SSR进行拉普拉斯变换得到
{s~x(x)=A~x(s)+b~u(s)~y(s)=cT~x(s)+d~u(s)
消去~x(s)得到
~y(s)=[cT(sI−A)−1b+d]~u(s)
由系统的单位冲激响应的拉普拉斯变换即是系统的传递函数,得
G(s)=cT(sI−A)−1b+d=cTadj(sI−A)−1det(sI−A)b+d
2.3.4 从传递函数到状态空间表示
n阶微分方程对应的TF待定系数最多有2n+1(见下边的形式),而对应的状态空间的待定系数有n2+2n+1个(A有n2个待定系数,b和c各有n个,d有1个),所以由传递函数求状态空间表示的结果肯定是不唯一。不过仍然定义了一些状态空间表示的标准型。
能控和能观标准型
假设有传递函数如下
G(s)=bnsn+bn−1sn−1+bn−2sn−2+⋯+b1s+b0sn+an−1sn−1+⋯+a1s+a0=^bn−1sn−1+^bn−2sn−2+⋯+^b1s+^b0sn+an−1sn−1+⋯+a1s+a0+bn=^N(s)D(s)+bn
其中^bi=bi−bnai。令^~y(s)=~y(s)−bn~u(s),则对应的状态转换矩阵如下:
˙x1=−a0y+b0u˙xi=−ai−1y+bi−1u+xi−1, i≥2
|
状态变量 |
A |
b |
c |
d |
| 能控标准型 |
x1=^~y(s)^N(s)=~u(s)^D(s)xi=˙xi−1, i≥2 |
⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣010⋯0001⋯0⋮⋮⋮⋱⋮000⋯1−a0−a1−a2⋯−an−1⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦ |
⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣00⋮01⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦ |
⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣^b0^b1⋮^bn−2^bn−1⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦ |
bn |
| 能观标准型 |
˙x1=−a0y+b0u˙xi=−ai−1y+bi−1u+xi−1, i≥2 |
⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣00⋯0−a010⋯0−a101⋯0−a2⋮⋮⋱⋮⋮00⋯1−an−1⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦ |
⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣^b0^b1⋮^bn−2^bn−1⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦ |
⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣00⋮01⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦ |
bn |
- A的形式都是友矩阵(线代忘光了不知道这意味着啥)。
- 此处没有讲解能控和能观,要等到第8章才会展开这部分内容。
对角和约当标准型
对角标准型
如果传递函数有n个不同的极点,则可通过部分因式分解将其改写为:
G(s)=bn+c1s−p1+c2s−p2+⋯+cns−pn
其中ci可由留数定理确定:ci=lims→pi(s−pi)G(s)。令状态变量为~xi(s)=~u(s)s−pi,则状态空间表示为
A=⎡⎢
⎢
⎢
⎢
⎢⎣p10⋯00p2⋯0⋮⋮⋱⋮00⋯pn⎤⎥
⎥
⎥
⎥
⎥⎦,b=⎡⎢
⎢
⎢
⎢⎣11⋮1⎤⎥
⎥
⎥
⎥⎦,c=⎡⎢
⎢
⎢
⎢⎣c1c2⋮cn⎤⎥
⎥
⎥
⎥⎦,d=bn
约当标准型
如果有重极点,传递函数仍可通过部分因式分解改写为:
G(s)=c1,1(s−p1)n1+c1,2(s−p1)n1−1+⋯+c1,n1s−p1+c2,1(s−p2)n2+c2,2(s−p2)n2−1+⋯+c2,n2s−p2+⋯+cm,1(s−pm)nm+cm,2(s−pm)nm−1+⋯+cm,nms−pm+bn
其中ci,j可由留数定理确定:ci,j=1(j−1)!lims→pidj−1dsj−1(s−pi)jG(s)。则状态空间表示为
A=⎡⎢
⎢
⎢
⎢
⎢⎣J10⋯00J2⋯0⋮⋮⋱⋮00⋯Jm⎤⎥
⎥
⎥
⎥
⎥⎦,b=⎡⎢
⎢
⎢
⎢⎣b1b2⋮bm⎤⎥
⎥
⎥
⎥⎦,c=⎡⎢
⎢
⎢
⎢⎣c1c2⋮cm⎤⎥
⎥
⎥
⎥⎦,d=bn
其中
Ji=⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣pi10⋯000pi1⋯00⋮⋮⋮⋱⋮⋮000⋯10000⋯pi1000⋯0pi⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦,bi=⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣00⋮01⎤⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦,ci=⎡⎢
⎢
⎢
⎢
⎢⎣ci,1ci,2⋮ci,ni⎤⎥
⎥
⎥
⎥
⎥⎦
对应状态变量
~xi,ni(s)=~u(s)s−pi→˙xi,ni=pixi,ni+u~xi,ni−1(s)=~u(s)(s−pi)2=~xi,ni(s)s−pi→˙xi,ni−1=pixi,ni−1+xi,ni~xi,ni−2(s)=~u(s)(s−pi)3=~xi,ni−1(s)s−pi→˙xi,ni−2=pixi,ni−2+xi,ni−1⋮→⋮~xi,1(s)=~u(s)(s−pi)ni=~xi,2(s)s−pi→˙xi,1=pixi,1+xi,2
2.3 系统的两种图形化表示方法
2.3.1 框图
-
框图化简
-
并联:G=G1+G2
-
串联:G=G2G1(G2连在G1之后)
-
反馈:Gc=G1+HG(负反馈为+,正反馈则要改成-)
-
移动求和点:~y=G~r+~d=G(~r+G−1~d)
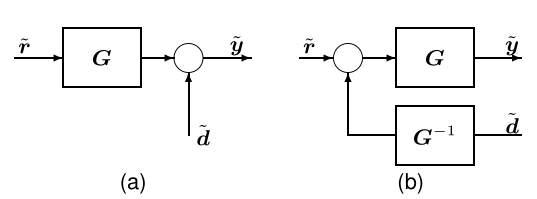
-
移动分支点:添加G或者G−1
2.3.2 信号流图








【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步