【Convex Optimization】Convex Optimization Basics

『Convex Optimization Basics - YouTube』

---

 【Convex Sets】Some properties:

1. The empty set ∅ and  ℝd are both convex.
2. Preserved by scaling and translation.
3. Intersections of convex sets are convex.

【Convex Functions】

Some properties:

1. Any local minimum is a global minimum.
2. Where it exists, the Hessian is positive semi-definite.
3. Level sets are convex.
4. a·f(x) + b·g(x) is convex for convex f,g and a,b > 0.
5. max(f(x), g(x)) is convex for convex f(x) and g(x).

【Convex Optimization Terminology】

1. optimization variable
2. objective / cost function
3. inequality constraints
4. equality constraints
5. feasible
6. optimal value
7. optimal point
8. active
9. inactive

【Why Convex Optimization?】

1. Contains various types of problems, e.g., many ML and OR tasks.
2. Repeatability: different runs give the same results.
3. Some convex problems can be solved in polynomial time.

• However, lots of important problems aren't convex: neural networks, k-means, most Bayesian inference.

【Duality】

The max-min inequality: the max of the minima ≤ the min of the maxima

E.g.: minimize f0(x) subject to fj(x) ≤ 0 ∀j ∈ 1,2,...,J

• Lagrange multipliers: λ = [λ₁, ..., λ_J]^T≥ 0 ⇒ L(x, λ) = f₀(x) + Σ_jλ_jf_j(x) ⇒ Objective: min_xP(x) = min_xmax_λ≥0L(x, λ)
• Weak duality: D(λ) = min_xL(x, λ) ("dual" objective)
• Duality gap: tightness of lower bound min_xP(x) - max_λD(x)
• Strong duality: duality gap = 0

【Linear Programming】

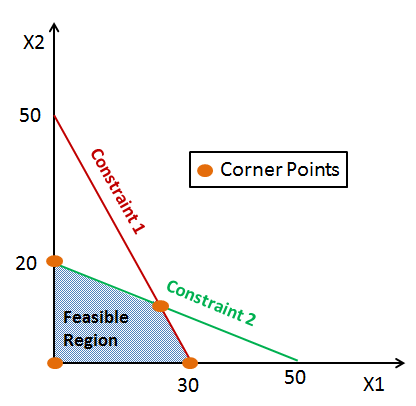
 LP examples:

1. Minimize food costs subject to nutrition constraints.
2. Maximize factory profit subject to materials available.
3. Max network flow subject to link capacity and equilibrium.
4. Farmer maximizes yield subject to land and fertilizer usage.

LP solution approaches:

• Simplex Algorithm: "greedy" strategy, earliest and most commonly used; requires exponential complexity.
• The Ellipsoid Method: only solves feasibility problem, appealing if testing violations is easy
• Interior-Point Methods: many hybrid methods, active research area

Dual of LP: primal-dual

【Quadratic Programming】

quadratic objective, linear constraints

E.g.:

• Support vector machines
• Constrained least squares
• Model predictive control

Dual of QP