空心电抗器的matlab建模与性能仿真分析

1.课题概述

        空心电抗器是一种无铁芯的电感元件，主要由一圈或多圈导线绕制在非磁性材料制成的空心圆筒或其他形状的骨架上构成。其工作原理基于法拉第电磁感应定律，当交流电通过电抗器时，会在电抗器的绕组中产生自感电动势，阻碍电流的变化，因此起到限制电流、滤波、吸收谐波和提高功率因数的作用。由于电抗器采用的是多包封多层次并联的结构设计的，而且每一层的又有若干个金属导线并联环绕构成，因此，在计算电抗器损耗的时候需要首先计算单个导线的涡流损耗。

 

2.系统仿真结果

 

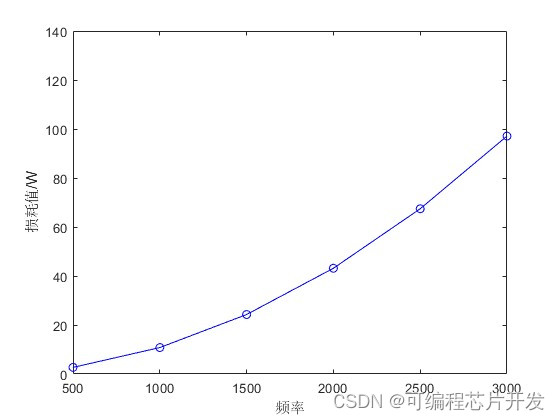
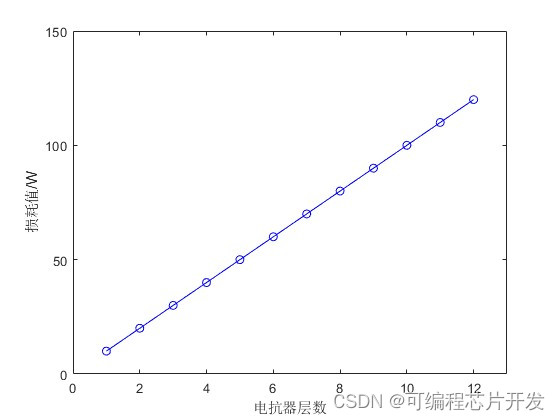
3.核心程序与模型

版本：MATLAB2022a

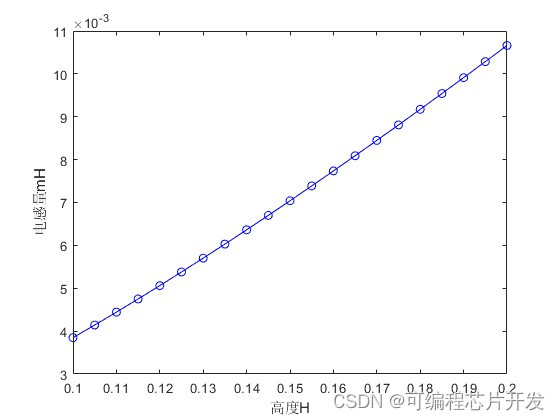
%不同高度的分析
Hs = [100:5:200]/1000;
for i = 1:length(Hs)
    i
    %高度H
    H = Hs(i);%mm
    %半径R
    R = 156.56/1000;
    %单位长度匝数n
    n = 26;
    %磁导率
    u = 4*pi*10^(-7);
    Zi= H;
    Z2= 0;
    %自感
    V1 = funcf(R,R,Zi);
    V2 = funcf(R,R,0);
    L1(i) = double(4*pi*u*(R)^3*n^2*(V1-V2)); 
end
figure;
plot(Hs,1000*L1,'b-o');
xlabel('高度H');
ylabel('电感量mH');


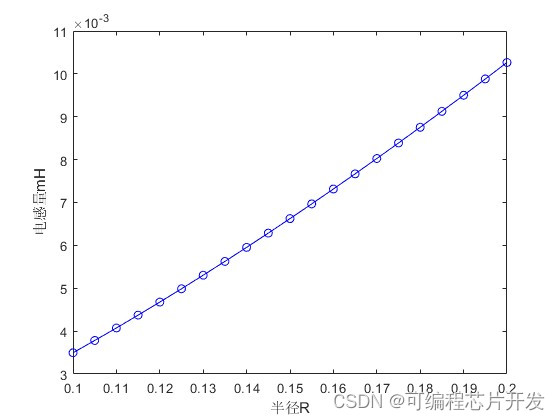
%不同半径的分析
Rs = [100:5:200]/1000;
for i = 1:length(Rs)
    i
    %高度H
    H = 150.5/1000;%mm
    %半径R
    R = Rs(i);
    %单位长度匝数n
    n = 26;
    %磁导率
    u = 4*pi*10^(-7);
    Zi= H;
    Z2= 0;
    %自感
    V1 = funcf(R,R,Zi);
    V2 = funcf(R,R,0);
    L2(i) = double(4*pi*u*(R)^3*n^2*(V1-V2)); 
end
figure;
plot(Rs,1000*L2,'b-o');
xlabel('半径R');
ylabel('电感量mH');



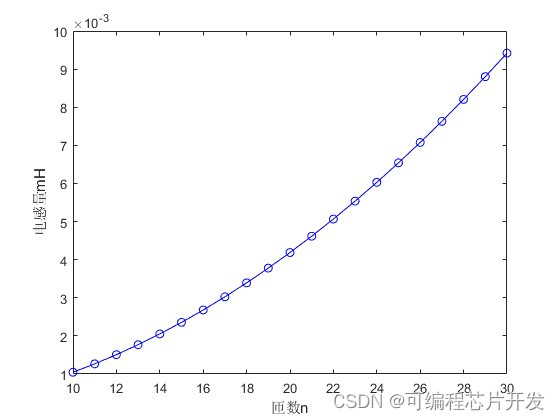
%不同匝数的分析
ns = [10:1:30];
for i = 1:length(ns)
    i
    %高度H
    H = 150.5/1000;%mm
    %半径R
    R = 156.56/1000;
    %单位长度匝数n
    n = ns(i);
    %磁导率
    u = 4*pi*10^(-7);
    Zi= H;
    Z2= 0;
    %自感
    V1 = funcf(R,R,Zi);
    V2 = funcf(R,R,0);
    L3(i) = double(4*pi*u*(R)^3*n^2*(V1-V2)); 
end

figure;
plot(ns,1000*L3,'b-o');
xlabel('匝数n');
ylabel('电感量mH');

　　

4.系统原理简介

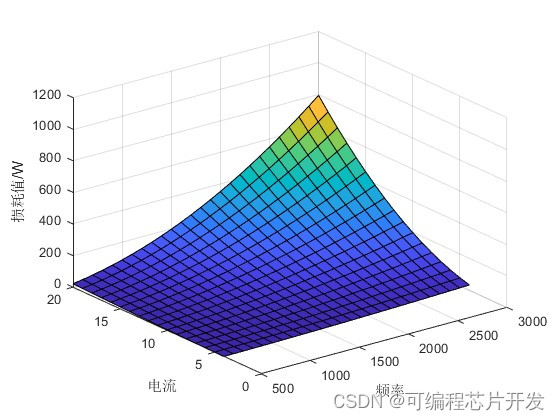
       电抗器的损耗是由三种不同类型的损耗构成的，包括涡流损耗，电阻损耗以及环流损耗三种类型，下面分别对三种损耗的计算过程进行介绍。

 

        涡流损耗主要是由于电抗器中处于交变磁场影响范围内的线圈产生的涡流而导致的损耗。又由于电抗器是由多个导线绕成，因此我们先分析单个圆形导线的涡流损耗。如图所示，其为单个导线的横截面。

 

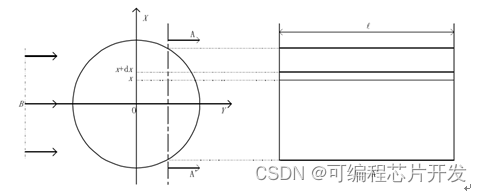
涡流损耗可以通过如下计算公式表示：

 

 

 

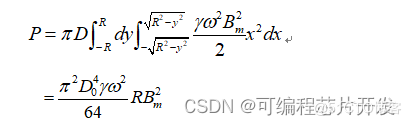
    电抗器的阻抗损耗是其最基本的一种损耗表现形式，其计算公式如所示：

 

 

 

       在电抗器正常工作过程中，由于交变磁场的影响，会导致电抗器中不同层次之间的线圈的漏电势不一样，那么就会导致各个线圈之间会产生相应的环流，并导致环流损耗。其计算公式可以表示为：

 

 

 

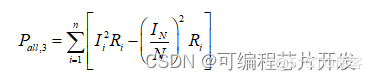
         通常情况下，电阻损耗是电抗器中的总损耗，一般情况下，随着电抗器半径的增加，其电阻损耗也会增加；而涡流损耗则不仅和半径有关，其还和电抗器的磁场、绕线匝数有关，其随着半径的增加而减少；环流损耗则与各层的电流相关。