基于模糊PID控制器的的无刷直流电机速度控制simulink建模与仿真

1.课题概述

       基于模糊PID控制器的的无刷直流电机速度控制simulink建模与仿真。基于模糊PID控制器的无刷直流电机（Brushless Direct Current Motor, BLDCM）速度控制系统是一种融合了传统PID控制与模糊逻辑控制优势的智能控制策略，旨在提高BLDCM速度控制的动态响应、抗干扰能力和稳态精度。

 

2.系统仿真结果

 

 

 

 

 

 

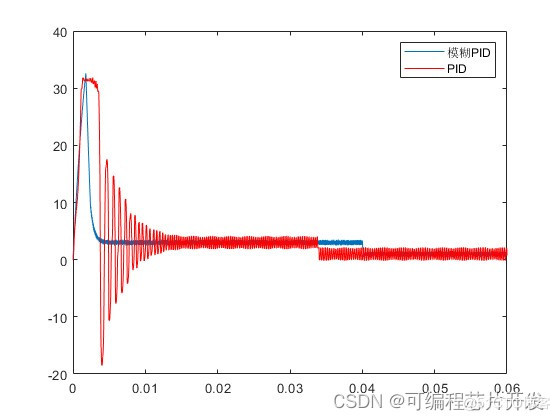
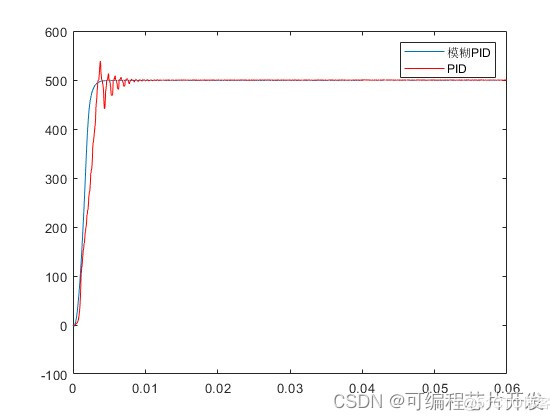
3.核心程序与模型

版本：MATLAB2022a

 

 

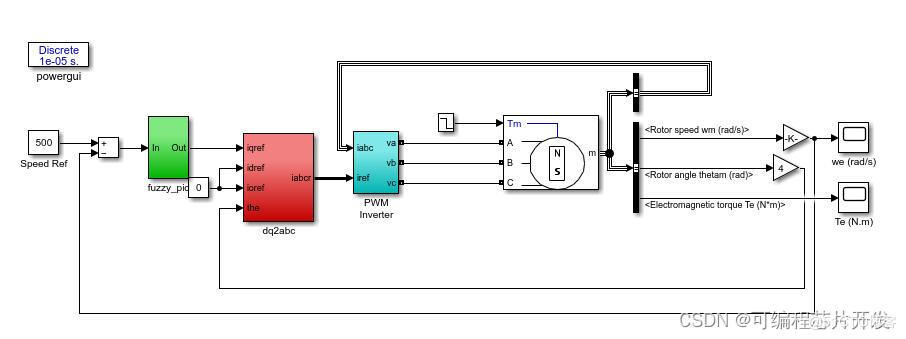
4.系统原理简介

4.1无刷直流电机模型与速度控制

无刷直流电机由定子绕组、永磁转子和电子换相器组成。其数学模型可简化为：

 

 

 

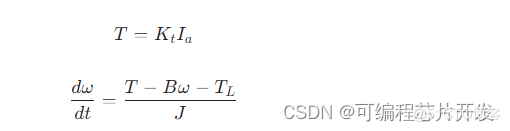
      其中，T 为电机电磁转矩，Kt​ 为扭矩系数，Ia​ 为定子相电流，ω 为电机角速度，B 为电机摩擦系数，TL​ 为负载转矩，J 为转动惯量。速度控制的目标是通过调节定子相电流 Ia​ 来实现电机转速 ω 的精确跟踪。

 

4.2 模糊PID控制器设计

        模糊PID控制器结合了PID控制的稳定性、易整定性和模糊逻辑控制的非线性适应性、语言描述优势，其结构通常包含模糊化、模糊推理、解模糊三个环节。

 

模糊化：将PID控制器的误差 e=r−ω （设定转速 r 与实际转速 ω 之差）和误差变化率 e˙=dtde​ 作为输入，通过隶属函数将其转化为模糊语言变量（如“负大”、“负中”、“负小”、“零”、“正小”、“正中”、“正大”）。

 

模糊推理：依据预先设计的模糊控制规则库，对模糊化后的误差和误差变化率进行模糊推理，得出PID参数（比例系数 Kp​、积分系数 Ki​、微分系数 Kd​）的模糊输出。

 

例如，典型模糊控制规则如下：

 

IF (Error is NB AND Derivative is NB) THEN (P is PB, I is NB, D is ZE)

...

IF (Error is ZE AND Derivative is PB) THEN (P is PM, I is ZE, D is PB)

其中，NB、NM、ZE、PS、PM、PB分别代表“负大”、“负中”、“零”、“正小”、“正中”、“正大”。

 

解模糊：将模糊输出通过中心平均法、重心法、最大隶属度法等解模糊算法转化为具体的PID参数值，用于后续的PID控制计算。

 

       基于模糊PID控制器的无刷直流电机速度控制系统巧妙地结合了PID控制与模糊逻辑控制的优点，通过模糊化、模糊推理、解模糊等步骤动态调整PID参数，实现对电机转速的精确、稳定控制。这种系统具有良好的动态响应、抗干扰能力和稳态精度，适用于各种工况下的BLDCM速度控制应用。