基于粒子群算法的分布式电源配电网重构优化matlab仿真
1.课题概述
基于粒子群算法的分布式电源配电网重构优化。通过Matlab仿真,对比优化前后
1.节点的电压值
2.线路的损耗,这里计算网损
3.负荷均衡度
4.电压偏离
5.线路的传输功率
6.重构后和重构前开关变化状态
2.系统仿真结果
1.节点的电压值
15.0000 + 0.0000i
14.9761 + 0.0002i
14.8564 + 0.0014i
14.8396 + 0.0000i
14.8257 - 0.0006i
14.7965 - 0.0093i
14.7898 - 0.0164i
14.3003 - 0.3734i
14.2857 - 0.3291i
14.2937 - 0.3099i
14.2968 - 0.3073i
14.3781 - 0.4659i
14.3691 - 0.4669i
14.2306 - 0.2775i
14.2385 - 0.2765i
14.2389 - 0.2553i
14.2331 - 0.2024i
14.2325 - 0.1839i
14.9747 - 0.0003i
14.4088 - 0.4626i
14.3907 - 0.4526i
14.4048 - 0.4598i
14.7643 - 0.0073i
14.5812 - 0.0374i
14.4344 - 0.0587i
14.7945 - 0.0095i
14.7931 - 0.0096i
14.3626 - 0.0771i
14.3669 - 0.0753i
14.3191 - 0.0713i
14.2603 - 0.1246i
14.2465 - 0.1425i
14.2405 - 0.1634i
2.线路的损耗,这里计算网损
PLoss0 =
139.9155
PLoss1 =
56.7952
损耗降低百分比:
ans =
59.4075
3.负荷均衡度
ans =
0.0196
4.电压偏离
ans =
27.8995
5.线路的传输功率
Powers =
22.5049
22.5231
22.5006
22.5004
22.5006
22.5000
22.9657
22.5014
22.5003
22.5001
22.5765
22.5000
22.5373
22.5001
22.5004
22.5008
22.5003
22.5000
22.6966
22.5004
22.5001
22.5129
22.5236
22.5152
22.5000
22.5000
22.6011
22.5000
22.5036
22.5033
22.5007
22.5004
22.5036
22.5012
22.5002
22.5005
22.5048
6.重构后和重构前开关变化状态
Switch0 =
7 1 3 2 16
Switch1 =
2 4 4 4 15
swicths =
2 4 4 4 15
3 5 5 5 16
3.核心程序与模型
版本:MATLAB2017B
figure;
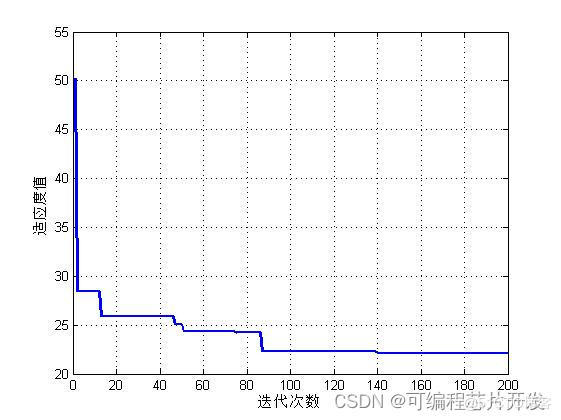
plot(objs,'linewidth',2);
xlabel('迭代次数');
ylabel('适应度值');
grid on
%1、节点的电压值
Node_volgates{indxmin2}
%2、线路的损耗,这里计算网损
%重构前
PLoss0 = Loss0(indxmin_,:)
%重构后
PLoss1 = min(Loss1)
disp('损耗降低百分比:');
100*abs(PLoss0-PLoss1)/PLoss0
%负荷均衡度,这里均衡采用了方差来计算,值越小,均衡度越高
fobj2(indxmin)
%电压偏离
fobj1(indxmin)
%3、线路的传输功率
case33;
Node_voltage = Node_volgates{indxmin2};
for iii = 1:length(Matrix1)
Powers(iii,1) = abs((abs(Node_voltage(Matrix1(iii,2))-Node_voltage(Matrix1(iii,3))))^2/(Matrix1(iii,4))+Rz);
end
Powers
%4、重构后和重构前开关变化状态
%重构前
Switch0 = Best_pso_(indxmin_,:)
%重构后
Switch1 = Best_pso(indxmin2,:)
%5、如果出现故障,及一条线路断开之后开关变化状态
%这里进行断开支路测试
for i = 1:Swicth
swicths(:,i) = [Matrix1(Switch1(i),2:3)]';
end
swicths
02_054m
4.系统原理简介
分布式电源配电网重构(Distribution Network Reconfiguration,DNR)是一个重要的电力系统优化问题,旨在通过改变配电网中的开关状态,以最小化网络损耗、提高供电可靠性和优化分布式电源的接入效益。粒子群优化算法(Particle Swarm Optimization, PSO)作为一种启发式全局优化方法,被广泛应用于解决此类复杂优化问题。
4.1基本PSO算法原理
在PSO中,每个粒子表示配电网重构的一种可能解(即一种开关状态组合),其位置矢量X_i代表第i个粒子所对应的解空间中的解。每个粒子具有速度矢量V_i,用于更新其位置:
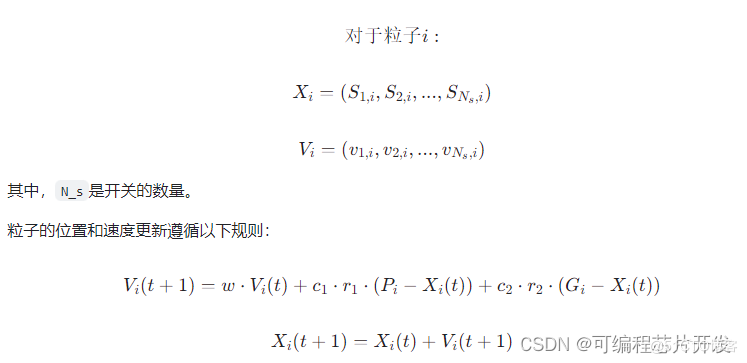
w是惯性权重,用于平衡全局搜索和局部搜索。
c_1 和 c_2 是加速常数,控制个体最优解(P_i)和全局最优解(G_i)对当前粒子的影响。
r_1 和 r_2 是随机变量,在[0, 1]之间,用于引入随机性。
P_i 是粒子i的历史最优位置(对应最低目标函数值的开关状态组合)。
G 是整个种群中的全局最优位置(所有粒子经历过的最优开关状态组合)。
4.2配电网重构的目标函数
在基于粒子群算法的分布式电源配电网重构优化问题中,目标函数通常结合了多个评价指标以达到综合最优。这里主要考虑以下三个关键因素:
节点电压偏离(Voltage Deviation) 节点电压偏离反映了配电网络重构后各节点实际电压与额定电压之间的差异。其数学表示通常采用均方误差的形式:
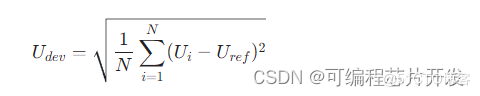
其中,Ui 是第 i 个节点的实际电压,Uref 是参考电压或额定电压,N 是总节点数。
线路负荷均衡度(Load Balance Index) 线路负荷均衡度衡量的是整个配电网内各线路负载分布的均匀程度。一种可能的度量方法是计算所有线路负荷与其平均值的标准差:
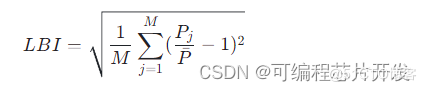
其中,Pj 表示第 j 条线路的功率负荷,ˉPˉ 是所有线路负荷的平均值,M 是线路总数。
线路损耗(Line Losses) 线路损耗包括电阻损耗和电抗损耗,在考虑分布式电源接入的情况下,需要根据重构后的网络拓扑结构和运行状态计算总的线路损耗:
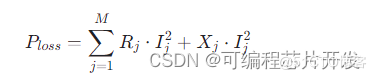
这里,Rj 和Xj 分别为第 j 条线路的电阻和感抗,Ij 是通过该线路的电流。
将上述三个指标整合成一个复合目标函数,可以采用加权和的方式表达:
Ttttttttttttttttt666666666
粒子群算法则用于求解此复合目标函数的最小化问题,通过不断迭代更新每个粒子(即潜在的网络重构方案)的位置和速度,最终找到一组最优的开关状态组合。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号