基于鱼群算法的散热片形状优化matlab仿真
1.课题概述
使用浴盆曲线进行空隙外形的模拟，然后通过优化，计算得到最优的浴盆曲线的各个参数，从而计算出最优的R值。浴盆曲线函数如下所示：
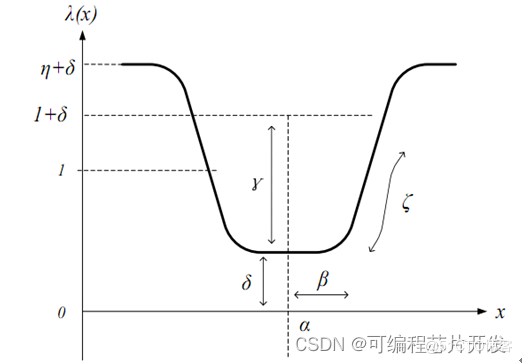
从上面的仿真结果可知，直接对目标函数进行优化，仿真速度非常慢，这里我们使用浴缸曲线结合鱼群算法进行优化。从而得到最佳的孔隙度值和H对应的R值。对于浴缸函数，首先可以将部分参数设置为0，从而简化参数，这里，我们假设为0.
函数可以简化为：
更详细原理可参考文献：
2.系统仿真结果
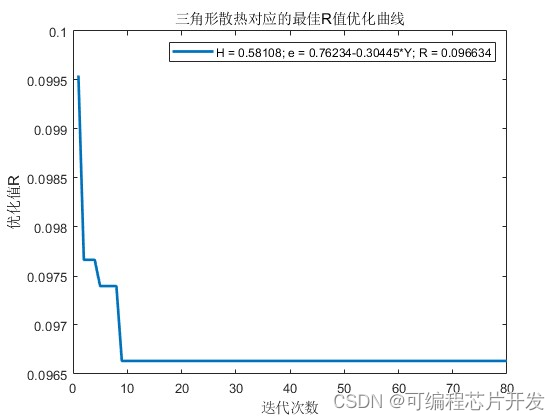
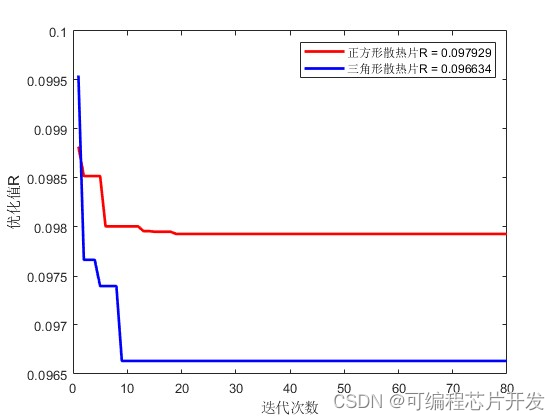
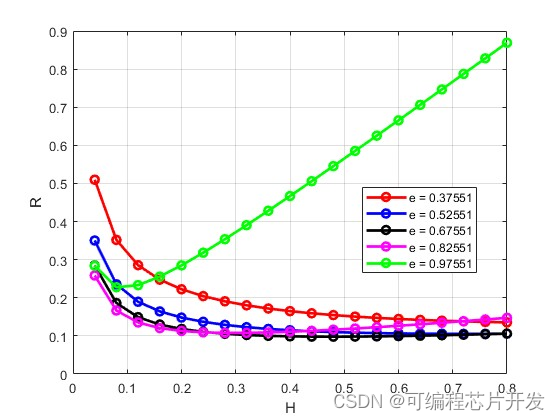
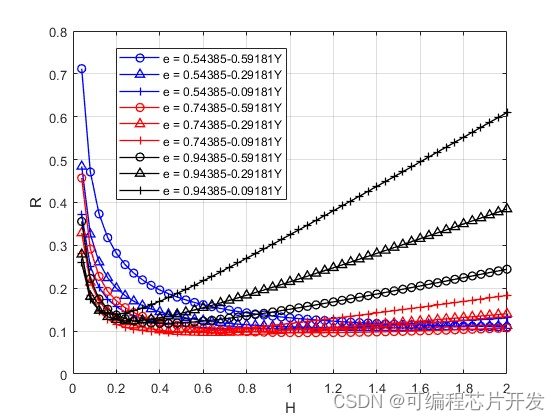
3.核心程序与模型
版本：MATLAB2022a
X = func_init(Num_Fish,Value_Limit,Value_Limit2);
Value_Limit_Store = Value_Limit2(1:Ker,:);
gen = 1;
BestY = -1*ones(1,Iteration); %最优的函数值
BestX = -1*ones(Ker,Iteration); %最优的自变量
besty = -9999; %最优函数值
[Y] = func_consistence(X);
while(gen<=Iteration)
gen
for J=1:Num_Fish
J
%聚群行为
[Xi1,Yi1]=func_Fish_swarm (X,J,Dist_Visual,step,crowd,Num_search,Value_Limit_Store,Y);
%追尾行为
[Xi2,Yi2]=func_Fish_Follow(X,J,Dist_Visual,step,crowd,Num_search,Value_Limit_Store,Y);
if Yi1>Yi2
X(:,J)=Xi1;
Y(1,J)=Yi1;
else
X(:,J)=Xi2;
Y(1,J)=Yi2;
end
end
[Ymax,index]=max(Y);
if Ymax > besty
besty = Ymax;
bestx = X(:,index);
BestY(gen) = Ymax;
[BestX(:,gen)] = X(:,index);
else
BestY(gen) = BestY(gen-1);
[BestX(:,gen)] = BestX(:,gen-1);
end
gen = gen + 1;
end
figure
plot(1:Iteration,1./BestY,'-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
xlabel('迭代次数');
ylabel('优化值');
disp(['最优解X：',num2str(bestx' ,'%1.5f ')]);
disp(['最优解Y：',num2str(1/besty,'%1.5f ')]);
save test.mat Iteration bestx besty BestY
alpha = 0;
beta = bestx(2);
gama = bestx(4);
siga = bestx(3);
delt = 0;
ling = bestx(1);
t = -2.5:0.02:2.5;
for i = 1:length(t)
if abs(i-alpha) >= beta
b(i) = -(abs(t(i) - alpha)-beta)^siga/gama;
else
b(i) = 0;
end
lemda(i) = delt + ling*(1-exp(b(i)));
end
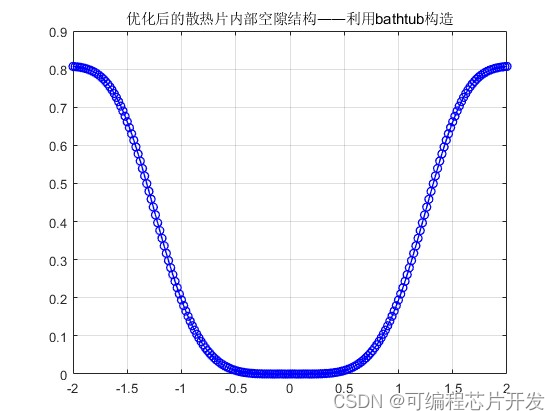
figure;
plot(t,lemda,'b-o','LineWidth',1);
title('优化后的散热片内部空隙结构——利用bathtub构造');
grid on
02_014m
toc
4.系统原理简介
鱼群算法（Fish Swarm Algorithm，FSA）是一种模拟自然界中鱼群行为的优化算法，具有全局搜索能力强、收敛速度快等优点。基于鱼群算法的散热片形状优化，是通过引入鱼群算法来寻找散热片最佳形状的一种方法。
4.1鱼群算法原理
鱼群算法通过模拟鱼群中个体的行为来实现寻优。在自然界中，鱼群往往呈现出一种自组织、自适应的行为特征，如聚群、避障、觅食等。鱼群算法将这些行为抽象为数学模型，通过迭代计算来寻找最优解。在鱼群算法中，每个个体（鱼）的行为受以下三个规则影响：
（1）聚群规则：个体趋向于向邻近个体聚集，以保持群体凝聚力。数学上，这可以通过计算个体与邻近个体的平均距离来实现。
（2）避障规则：个体在游动过程中会避开障碍物，以保证生存空间。数学上，这可以通过计算个体与障碍物之间的距离来实现。
（3) 觅食规则：个体趋向于向食物丰富的区域游动，以获取更多食物。数学上，这可以通过计算个体的适应度值来实现。
4.2鱼群算法的流程
（1）初始化：设定鱼群规模、迭代次数等参数，随机生成初始鱼群。
（2）计算适应度值：根据散热片形状优化的目标函数，计算每个个体的适应度值。
（3）更新位置：根据聚群规则、避障规则和觅食规则，更新每个个体的位置。
（4）判断终止条件：判断是否达到最大迭代次数或满足其他终止条件。若满足，则输出最优解；否则，返回步骤（2）。
4.3 散热片形状优化数学模型
浴盆曲线函数如下所示：
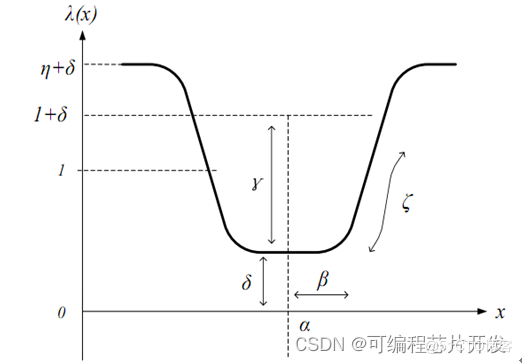
上述结果在优化过程中，可以表示为：
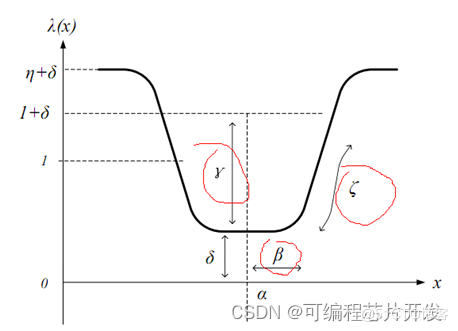
其余参数只改变浴缸曲线的位置，所以，这里我们只要对上面红色的三个参数和外部的H进行最优搜索即可。其对应的结果为：
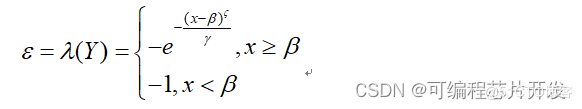
确定优化变量：选择散热片的形状参数作为优化变量。
建立目标函数：根据散热片性能评价指标，建立目标函数。
确定约束条件：根据散热片设计要求，确定约束条件。
初始化鱼群：设定鱼群规模和迭代次数，随机生成初始鱼群。
计算适应度值：根据目标函数和约束条件，计算每个个体的适应度值。
更新位置：根据聚群规则、避障规则和觅食规则，更新每个个体的位置。在更新过程中，需要考虑散热片的形状约束和制造工艺约束。可通过引入罚函数法或可行方向法来处理约束条件。
判断终止条件：判断是否达到最大迭代次数或满足其他终止条件。若满足，则输出最优解；否则，返回步骤（5）。
