基于MATLAB的SEIR传染病模型建模与仿真
1.课题概述
SEIR传染病模型是一种用于描述传染病传播过程的数学模型。这个模型将人群分为四类：易感者（Susceptible）、暴露者（Exposed）、感染者（Infectious）和康复者（Recovered），通过这四类人群之间的转化关系，来描述传染病的传播过程。通过matlab将这个过程进行建模与仿真。
2.系统仿真结果
3.核心程序与模型
版本：MATLAB2022a
% 初始化
%总人口
Npeople = 9e6;
% 感染人数
I_0 = 98;
% 暴露人数
E_0 = 20 * I_0;
% 康复人数 / 免疫人数
R_0 = 0;
% 易感人数
S_0 = Npeople - E_0 - I_0 - R_0;
% 初始状态向量
y0 = [S_0, E_0, I_0, R_0];
%模拟时间设定
%一年
days = 365;
h = 1;
%步长（1天）
tspan = 1:h:days;
% 使用ODE求解器进行模拟
% S:易感者, E:暴露者, I:感染者, R:康复者
[t,y] = ode45(@(t,y) func_beta2(t,y,Npeople,beta,delta,gamma), tspan, y0);
figure;
plot(t,y(:,1),'LineWidth',3);
hold on
plot(t,y(:,2),'LineWidth',3);
hold on
plot(t,y(:,3),'LineWidth',3);
hold on
plot(t,y(:,4),'LineWidth',3);
hold on
grid on
axis([0 days 0 10e6]);
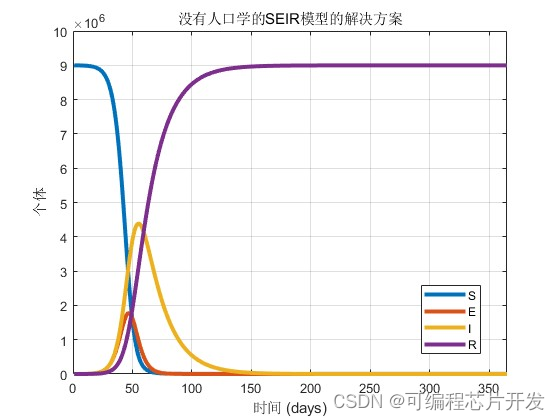
title('没有人口学的SEIR模型的解决方案');
xlabel('时间 (days)');
ylabel('个体');
legend('S','E','I','R');
figure;
plot(t,y(:,3),'g','LineWidth',3);
grid on
axis([0 days 0 5e6]);
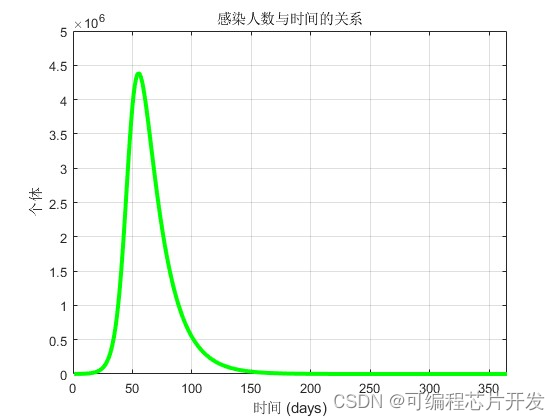
title('感染人数与时间的关系');
xlabel('时间 (days)');
ylabel('个体');
figure;
plot(t_w,y_w(:,1),'LineWidth',3);
hold on
plot(t_w,y_w(:,2),'LineWidth',3);
hold on
plot(t_w,y_w(:,3),'LineWidth',3);
hold on
plot(t_w,y_w(:,4),'LineWidth',3);
hold on
grid on
axis([0 days 0 10e6]);
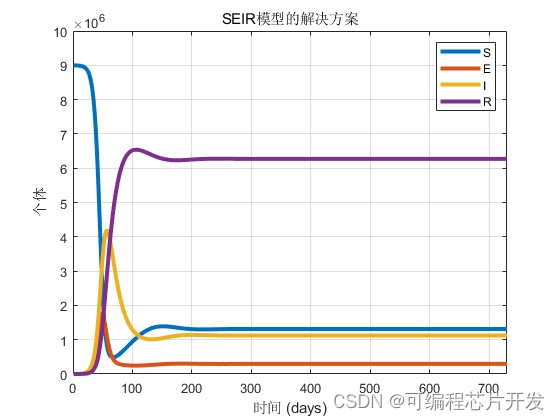
title('SEIR模型的解决方案');
xlabel('时间 (days)');
ylabel('个体');
legend('S','E','I','R');
figure;
plot(t_w,y_w(:,3),'LineWidth',3);
grid on
axis([0 days 0 4e6]);
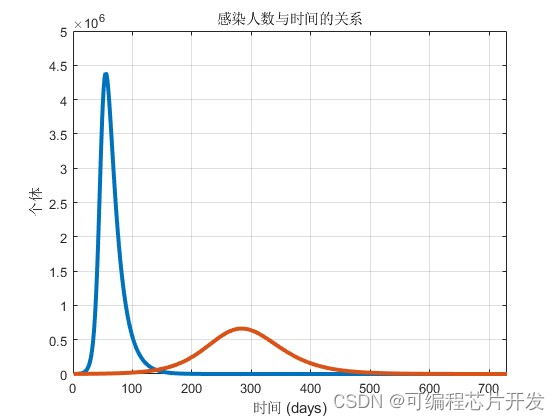
title('传染性个体数量与人口统计时间的关系');
xlabel('时间 (days)');
ylabel('个体');
0008
4.系统原理简介
SEIR传染病模型是一种用于描述传染病传播过程的数学模型。这个模型将人群分为四类：易感者（Susceptible）、暴露者（Exposed）、感染者（Infectious）和康复者（Recovered），通过这四类人群之间的转化关系，来描述传染病的传播过程。
一、模型假设
在考察地区的总人数N不变，即不考虑人口的流动。
人群分为易感者、暴露者、感染者和康复者四类。
易感者被感染者传染后成为暴露者，暴露者经过一定时间的潜伏期后成为感染者，感染者康复后成为康复者。
康复者对原病毒具有免疫力，不再被感染。
二、符号说明
N：总人口数
S(t)：t时刻易感者人数
E(t)：t时刻暴露者人数
I(t)：t时刻感染者人数
R(t)：t时刻康复者人数
β：感染率，表示一个感染者平均每天能传染给多少个易感者
σ：潜伏期的倒数，即每天有多少比例的暴露者转化为感染者
γ：康复率，表示每天有多少比例的感染者康复
Λ：人口输入率，假设每天有Λ个新个体进入考察地区，这些新个体都是易感者。
三、模型建立
根据模型假设和符号说明，我们可以建立以下微分方程来描述SEIR模型的传播过程：
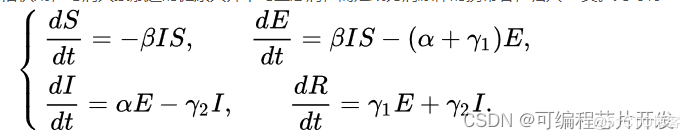
仍有守恒关系 S(t) + E(t) + I(t) + R(t) = 常数，病死者可归入 R 类。潜伏期康复率 γ1 和患者康复率 γ2 一般不同。潜伏期发展为患者的速率为 α。与 SIR 模型相比，SEIR 模型进一步考虑了与患者接触过的人中仅一部分具有传染性的因素，使疾病的传播周期更长。疾病最终的未影响人数 S∞ 和影响人数 R∞ 可通过数值模拟得到。
其中，第一个方程表示易感者人数的变化率等于新增的易感者人数减去被感染者传染的易感者人数；第二个方程表示暴露者人数的变化率等于被感染者传染的易感者人数减去转化为感染者的暴露者人数；第三个方程表示感染者人数的变化率等于转化为感染者的暴露者人数减去康复的感染者人数；第四个方程表示康复者人数的变化率等于康复的感染者人数。
四、参数估计与模型求解
为了求解SEIR模型，我们需要对模型参数进行估计。这些参数包括感染率β、潜伏期倒数σ和康复率γ。通常，我们可以通过疫情数据来估计这些参数。具体地，我们可以使用最小二乘法或其他优化算法来拟合疫情数据，从而得到参数的估计值。得到参数的估计值后，我们就可以使用数值方法（如欧拉法、龙格-库塔法等）来求解SEIR模型的微分方程，从而得到各类人群随时间的变化情况。
五、模型应用与预测
SEIR模型可以用于预测传染病的传播趋势和评估防控措施的效果。通过调整模型参数，我们可以模拟不同场景下传染病的传播情况，从而为制定防控策略提供依据。例如，我们可以模拟不同感染率、潜伏期和康复率下传染病的传播情况，以评估不同防控措施的效果。此外，我们还可以使用SEIR模型来预测未来一段时间内的疫情发展趋势，以便及时采取应对措施。
