支路电气介数的matlab仿真,并对比HVDC,FACTS-TCSC,FACTS-UPFC

1.课题概述

        支路电气介数的matlab仿真,并对比HVDC,FACTS-TCSC,FACTS-UPFC。HVDC、FACTS（包含TCSC和UPFC）三种简化模型在电气介数计算中的体现形式为：对测试系统，可以在系统任意数量和位置的线路上对以上三种简化模型进行选择。得出考虑三种模型后的系统中支路和节点的电气介数计算值和分布情况。

 

2.系统仿真结果

 

 

 

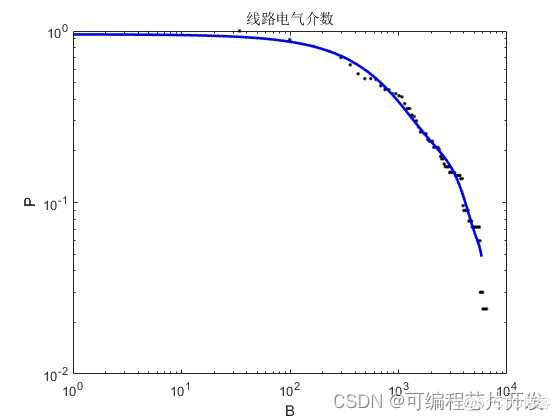
        节点/支路的电气介数的累积分布在双对数坐标下应该会出现幂律的表现形式。若不出现幂律分布，则很难说明电网中存在少数具有很高电气介数的节点和支路。

 

 

 

 

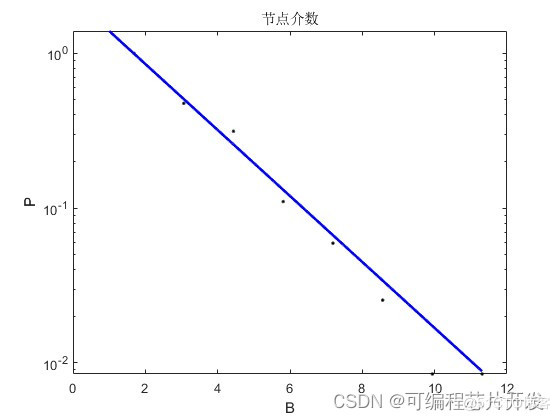
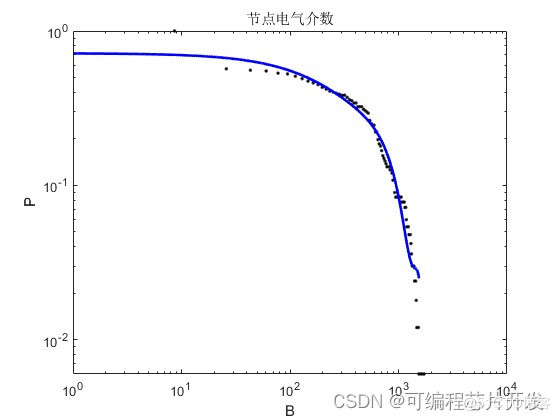
3.核心程序与模型

版本：MATLAB2022a

 

                            %计算wij
                            SG        = GEN(i,2)/mpc.baseMVA; 
                            SL        = BUS(L(j),3)/mpc.baseMVA;
                            w(k,j)    = min(SG,SL);

                            for l = 1:length(FK)
                                ll = FK(l);
                                %计算Pmn
                                Gs1_Ind1  = find(BRANCH(:,1) == G(i));
                                Gs1_Ind2  = find(BRANCH(:,2) == G(i));
                                Gs1_Ind   = unique([Gs1_Ind1;Gs1_Ind2]);
                                Pmn(k,ll) = F(k)*(F(k)/sum(F(Gs1_Ind)));   
                                %计算P
                                P(k,ll)   = F(k); 
                            end

                            tmps(i,j) = w(k,j)*Pmn(k,ll)/P(k,ll);   
                            W(k,j)    = w(k,j);


                   elseif k == L(j)   
                            %计算wij
                            SG        = GEN(i,2)/mpc.baseMVA; 
                            SL        = BUS(L(j),3)/mpc.baseMVA;
                            w(k,i)    = min(SG,SL);

                            for l = 1:length(FK)
                                ll = FK(l);
                                %计算Pmn
                                Gs1_Ind1  = find(BRANCH(:,1) == G(i));
                                Gs1_Ind2  = find(BRANCH(:,2) == G(i));
                                Gs1_Ind   = unique([Gs1_Ind1;Gs1_Ind2]);
                                Pmn(k,ll) = F(k)*(F(k)/sum(F(Gs1_Ind)));   
                                %计算P
                                P(k,ll)   = F(k); 
                            end

                            tmps(i,j) = w(k,i)*Pmn(k,ll)/P(k,ll);   
                            W(k,i)    = w(k,i);

                   else
                            %计算wij
                            SG        = GEN(i,2)/mpc.baseMVA; 
                            SL        = BUS(L(j),3)/mpc.baseMVA;
                            w(k,i)    = min(SG,SL);

                            for l = 1:length(FK)
                                ll = FK(l);
                                %计算Pmn
                                Gs1_Ind1  = find(BRANCH(:,1) == G(i));
                                Gs1_Ind2  = find(BRANCH(:,2) == G(i));
                                Gs1_Ind   = unique([Gs1_Ind1;Gs1_Ind2]);
                                Pmn(k,ll) = F(k)*(F(k)/sum(F(Gs1_Ind)));   
                                %计算P
                                P(k,ll)   = F(k); 
                            end

                            tmps(i,j) = w(k,i)*Pmn(k,ll)/P(k,ll);   
                            W(i,j)    = 0;  
................................................................
02_022m

　　

 

4.系统原理简介

         支路电气介数、高压直流输电（HVDC）、柔性交流输电系统（FACTS）中的可控串联补偿（TCSC）和统一潮流控制器（UPFC）是电力系统中的不同概念和技术。支路电气介数（Branch Electrical Betweenness）是电力系统网络分析中的一个指标，用于量化支路在功率传输中的重要性或介数中心性。它基于图论中的介数中心性概念，并考虑到电力系统的电气特性。支路电气介数高的支路在系统中承载着更多的功率流，因此对网络的稳定性和安全性有更大影响。

 

       支路m-n的电气介数计算式如下：

 

 

 

       节点k的电气介数计算式如下：

 

 

 

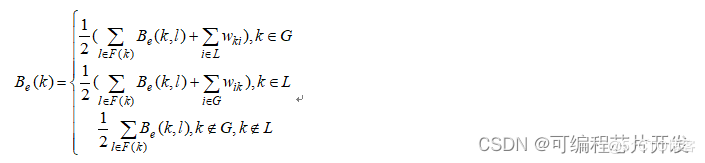
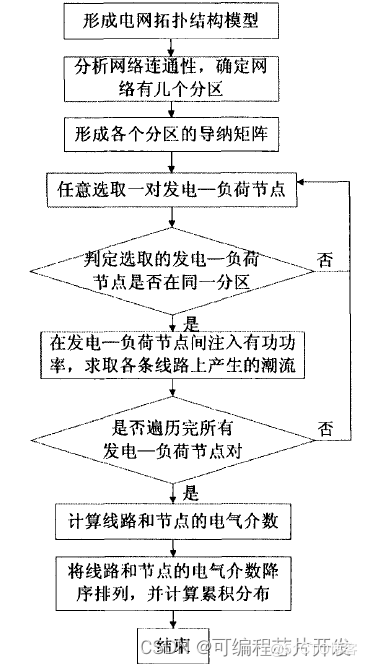
电气介数的计算流程：