软件工程个人项目作业

软件工程个人项目作业

项目 内容
这个作业属于哪个课程 2020春季计算机学院软件工程(罗杰 任健)
这个作业的要求在哪里 个人项目作业
我在这个课程的目标是 学习工程化开发软件
这个作业在哪个具体方面帮助我实现目标 软件的工程化
教学班级 006
项目地址 https://github.com/YANGHARAM/intersect

一.PSP表

PSP2.1 Personal Software Process Stages 预估耗时（分钟） 实际耗时（分钟）
Planning 计划 20 20
· Estimate 估计这个任务需要多少时间 10 10
Development 开发
· Analysis · 需求分析 (包括学习新技术) 30 40
· Design Spec 生成设计文档 30 40
· Design Review 设计复审 (和同事审核设计文档) 10 10
· Coding Standard 代码规范 (为目前的开发制定合适的规范) 10 20、
· Design 具体设计 20 30
· Coding 具体编码 40 70
· Code Review 代码复审 20 20
· Test 测试（自我测试，修改代码，提交修改） 30 50
Reporting 报告
·Test Report 测试报告 30 30
·Size Measurement 计算工作量 10 10
·Postmortem & Process Improvement Plan 事后总结, 并提出过程改进计划 20 20
·Size Measurement 合计 280 370

二.思路描述

输入的字符串用strtok_s函数分成5个字符串，然后这5个字符串转换为整数（int型）。
一个直线有两个点：(x1,y1),(x2,y2)这样的话他的倾斜a=(y1-y2)/(x1-x2).所以如果有交点的话两个直线相互不能平等。这就是两个直线的倾斜a1,a2不一样。a1!=a2.
用for函数比较输入的直线。然后不平等的话result++。但是如果交点重复的话不能加1.所以判断是不是交点重复。。最后输出result真。

三.设计实现过程

数据结构（直线）：
用直线的一般是:Ax+By+C=0.

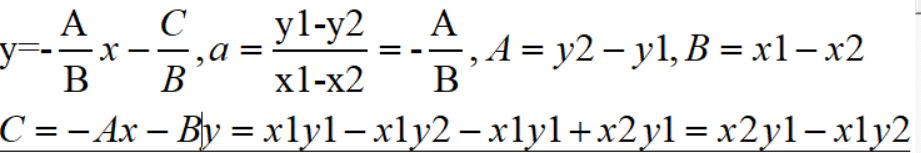
class Point {
public:
	string L;
	double x1;
	double y1;
	double x2;
	double y2;
	double A;//Ax+By+C=0
	double B;
	double C;
public:
	Point(){
		x1 = 0;
		y1 = 0;
		x2 = 0;
		y2 = 0;
		A = 0;
		B = 0;
		C = 0;
	}
	Point(string l,double X1, double Y1, double X2, double Y2) {
		L = l;
		x1 = X1;
		x2 = X2;
		y1 = Y1;
		y2 = Y2;
	}
};

交点判断：
用倾斜a公式判断两个直线是不是平等。如果不是的话就是有交点。

bool check(Point p1, Point p2) {
	double a1;
	double a2;
	a1 = (p1.y1 - p1.y2) / (p1.x1 - p1.x2);
	a2 = (p2.y1 - p2.y2) / (p2.x1 - p2.x2);
	if (a1 == a2)return false;
	else return true;
}

判断交点重复：
用for函数一个一个比较交点是不是重复，如果重复的话输出false就是不加1。

bool check_dot(dot D[],int d) {
	if (d == 1)return true;
	for (int i = 0; i < d-1; i++) {
		for (int j = 1 + i; j < d; j++) {
			if ((D[i].x == D[j].x) && (D[i].y == D[j].y))
				return false;
			else
				return true;

		}
	}

}

求交点:
用交点求公式。

void result_dot(dot &k,Point p1, Point p2) {
	double a = (p1.A * p2.B) - (p1.B * p2.A);
	if (((p1.B * p2.C) - (p1.C * p2.B)) == 0.0) {
		k.x = ((p1.B * p2.C) - (p1.C * p2.B));
	}
	else
	k.x = ((p1.B * p2.C) - (p1.C * p2.B)) / a;

	if (((p1.C * p2.A) - (p1.A * p2.C)) == 0.0) {

		k.y = ((p1.C * p2.A) - (p1.A * p2.C));
	}
	else
	k.y = ((p1.C * p2.A) - (p1.A * p2.C)) / a;
}

计算result：

double solve(Point p[],int n) {
	for (int i = 0; i < n; i++)
	{
		ABC(p[i]);
	}
	double result = 0;
	int d = 0;
	if (n == 1)return 0.0;
	for (int i = 0; i < n - 1; i++)
	{
		// 1 2 3 4 5
		for (int j = 1 + i; j < n; j++) {
			if (check(p[i], p[j]) && (p[i].L == "L") && (p[j].L == "L")) {
				result_dot(D[d++], p[i], p[j]);
				if(check_dot(D,d))
					result++;
			}

		}
	}
	return result;
}

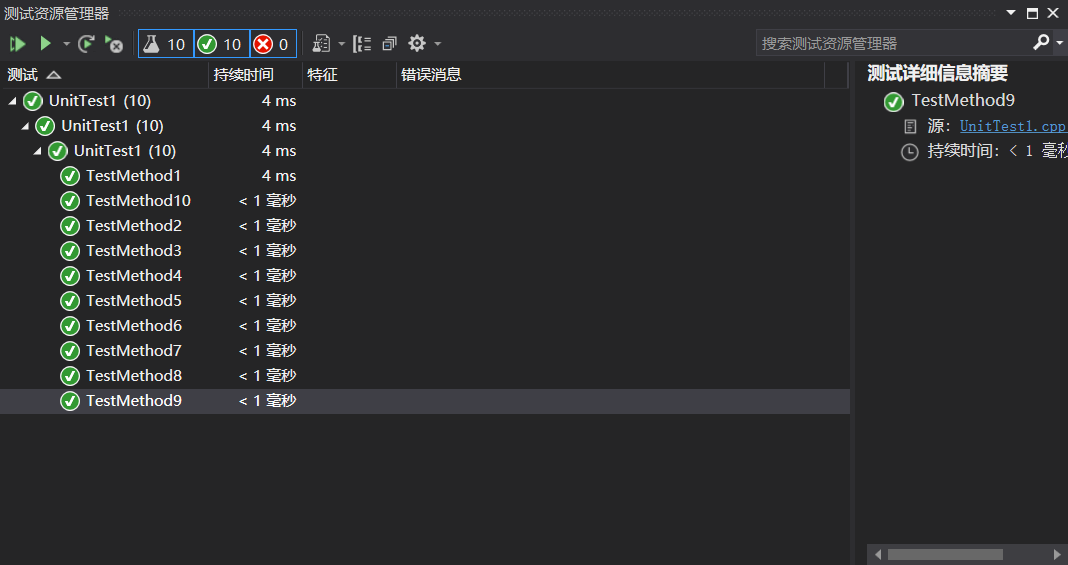
四.改进程序性能的过程

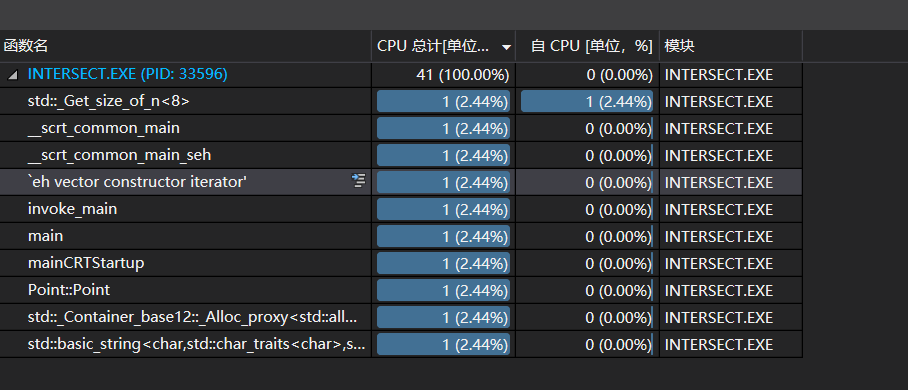
五.Code Quality Analysis

posted on 2020-03-10 18:20  梁河览  阅读(162)  评论(1)  编辑  收藏  举报

导航