【学习笔记】状压 dp
搬一张图:
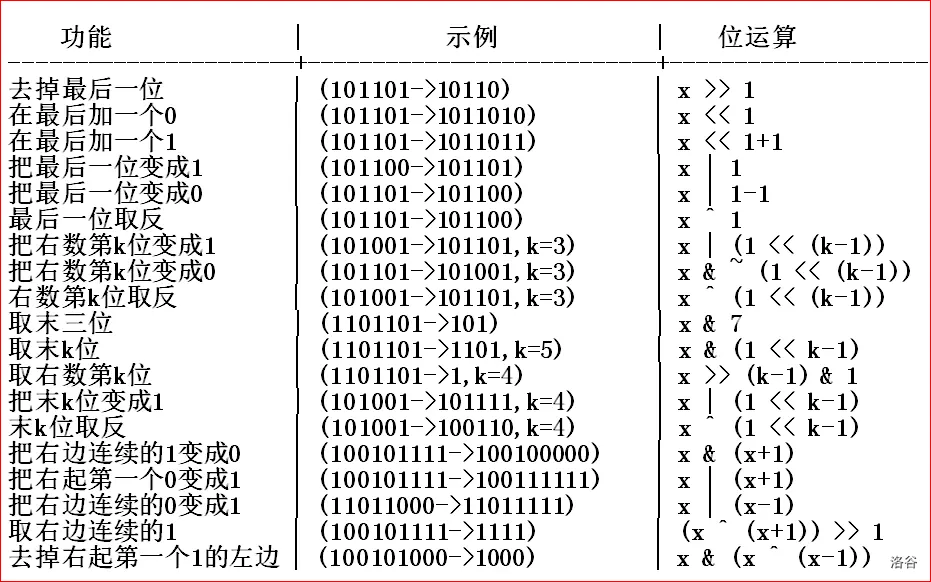
注:代码和实际内容可能会有较大偏差
状压 dp 模板题。先预处理出每一行可能的状态(就是本行互不侵犯),记 \(f_{i,j,s}\) 表示考虑到第 \(i\) 行,用了 \(j\) 个国王,此时的状态为 \(s\) 的方案数,记 \(cnt_s\) 为 \(s\) 二进制中 1 的个数,转移是枚举上一行的状态 \(t\),如果 \(s\) 和 \(t\) 两行可行就把 \(f_{i,j,s}\) 加上 \(f_{i-1,j-cnt_s,t}(cnt_s\le j)\)。
判断可行就看上下两行相邻列及同一列格子是否都有王,运用位运算:
- \(s\) 有王和 \(t\) 在同一列:
(s & t) != 0 - \(s\) 有王在 \(t\) 的左边一列:
(s & (t >> 1)) != 0 - \(s\) 有王在 \(t\) 的右边一列:
(s & (t << 1)) != 0
然后初始化是对于每个状态 \(s\),\(f_{1,cnt_s,s}=1\),时间复杂度 \(O(n^2cnt^2)\)。其中 \(cnt\) 为一行合法方案的数量。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 10;
const int K = 105;
const int M = 2005;
int n, kk, ts, sta[M], s[M], f[N][M][K];
void dfs(int k, int state, int sum) {
if (k >= n) {
sta[++ts] = state;
s[ts] = sum;
return;
}
dfs(k + 1, state, sum);
dfs(k + 2, state | (1 << k), sum + 1);
}
bool chk(int x, int y) {
if (sta[x] & sta[y]) return 0;
if ((sta[x] << 1) & sta[y]) return 0;
if (sta[x] & (sta[y] << 1)) return 0;
return 1;
}
signed main() {
cin >> n >> kk;
dfs(0, 0, 0);
for (int i = 1; i <= ts; i++) f[1][i][s[i]] = 1;
for (int i = 2; i <= n; i++)
for (int j = 1; j <= ts; j++)
for (int k = 1; k <= ts; k++) {
if (!chk(j, k)) continue;
for (int t = s[j]; t <= kk; t++)
f[i][j][t] += f[i - 1][k][t - s[j]];
}
int ans = 0;
for (int i = 1; i <= ts; i++)
ans += f[n][i][kk];
cout << ans;
return 0;
}
稍微复杂一点的板子。\(f_{i,j,k}\) 表示考虑到第 \(i\) 行,本行状态为 \(j\),上一行状态为 \(k\) 的最多炮兵。\(j,k\) 对于当行合法当且仅当每个炮兵离另外所有炮兵距离大于两个格子:!(i & (i << 1)) && !(i & (i >> 1)) && !(i & (i << 2)) && !(i & (i >> 2)),\(j,k\) 之间互相合法需要满足不在没有炮兵在同一列:!(i & j)。
转移很简单,就是枚举 \(i,j,k,s\),其中 \(s\) 为上两行的状态,与判断 \(j,k\) 合法类似地判断 \(j,s\) 和 \(k,s\) 两行是否合法,记得也得判断 \(s\) 关于本行是否合法,初始化:对于每个合法的状态 \(i\),\(f_{1,i,0}=cnt_i\)。
时间复杂度 \(O(ncnt^3)\),\(cnt\) 意义如上。
#include <bits/stdc++.h>
using namespace std;
const int N = 105;
const int M = 10;
int a[N], f[2][(1 << M) + 1][(1 << M) + 1], c[(1 << M) + 1];
bool vis[(1 << M) + 1];
inline int cal(int x) {
int res = 0;
while (x) res += x & 1, x >>= 1;
return res;
}
int main() {
int n, m; cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
char x; cin >> x;
a[i] = (a[i] << 1) | (x == 'P' ? 1 : 0);
}
for (int i = 0; i < (1 << m); i++)
if (!(i & (i << 1)) && !(i & (i >> 1)) && !(i & (i << 2)) && !(i & (i >> 2)))
vis[i] = true, f[1][i][0] = c[i] = cal(i);
for (int i = 2; i <= n; i++)
for (int st1 = 0; st1 < (1 << m); st1++) {
if (!vis[st1] || ((st1 | a[i]) != a[i])) continue;
for (int st2 = 0; st2 < (1 << m); st2++) {
if (!vis[st2] || (st1 & st2) || ((st2 | a[i - 1]) != a[i - 1])) continue;
for (int st3 = 0; st3 < (1 << m); st3++) {
if (vis[st3] && !(st1 & st3) && !(st2 & st3) && ((st3 | a[i - 2]) == a[i - 2]))
f[i & 1][st1][st2] = max(f[i & 1][st1][st2], f[(i - 1) & 1][st2][st3] + c[st1]);
}
}
}
int ans = 0;
for (int i = 0; i < (1 << m); i++)
for (int j = 0; j < (1 << m); j++)
ans = max(ans, f[n & 1][i][j]);
cout << ans;
return 0;
}
还是挺简单的。
\(f_{i,j}\) 表示当前到 \(i\),经过的点状态为 \(j\) 的最小距离,记 \((x1,y1)\) 和 \((x2,y2)\) 的距离为 \(dis(x1, y1, x2, y2)\),初始化\(f_{i,2^i}=dis(0,0,x_i,y_i)\)。
转移的思路也很明显:先枚举 \(i,j\) 然后枚举上一个点 \(k\),需要满足 \(k\) 在 \(j\) 中且 \(i\ne k\),然后类似最短路的取个 \(\min\) 即可,即:\(f_{i,j}=\min\{f_{i,j},f_{k,j-2^i}\}\)。
答案是所有取 \(\min\),本题记得用 double 类型,复杂度 \(O(n^22^n)\)。
#include <bits/stdc++.h>
using namespace std;
const int N = 16;
double x[N], y[N], f[N][1 << N];
double cal(double x1, double y1, double x2, double y2) {
return sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2));
}
int main() {
int n; cin >> n;
for (int i = 0; i < n; i++)
cin >> x[i] >> y[i];
memset(f, 127, sizeof(f));
for (int i = 0; i < n; i++)
f[i][1 << i] = cal(0, 0, x[i], y[i]);
for (int st = 1; st < (1 << n); st++) {
for (int i = 0; i < n; i++) {
if (!(st & (1 << i))) continue;
for (int j = 0; j < n; j++)
if ((st & (1 << j)) && (i != j))
f[i][st] = min(f[i][st], f[j][st - (1 << i)] + cal(x[i], y[i], x[j], y[j]));
}
}
double ans = 1e9;
for (int i = 0; i < n; i++)
ans = min(ans, f[i][(1 << n) - 1]);
printf("%.2lf", ans);
return 0;
}
这题和上题几乎一样,但不看数据范围可能还想不到状压 dp,就不再赘述了,但记得是单向边。
#include <bits/stdc++.h>
using namespace std;
const int N = 18;
int f[1 << N][N], dis[N + 1][N + 1];
int main() {
int n, m; cin >> n >> m;
for (int i = 1; i <= m; i++) {
int u, v, w; cin >> u >> v >> w;
u++, v++;
dis[u][v] = max(dis[u][v], w);
}
memset(f, -0x3f, sizeof(f));
f[1][1] = 0;
for (int i = 1; i < (1 << n); i++)
for (int j = 1; j <= n; j++) {
if (!(i & (1 << j - 1))) continue;
for (int k = 1; k <= n; k++)
if (!(i & (1 << k - 1)) && dis[j][k])
f[i | (1 << k - 1)][k] = max(f[i | (1 << k - 1)][k], f[i][j] + dis[j][k]);
}
int ans = 0;
for (int i = 0; i < (1 << n); i++)
ans = max(ans, f[i][n]);
cout << ans;
return 0;
}
P3092 [USACO13NOV] No Change G
发现硬币的范围很小,于是记 \(f_i\) 表示花费状态 \(i\) 下硬币最多能买到第几个物品,转移就是枚举每个在 \(i\) 中的物品 \(j\),从去掉 \(j\) 的状态 \(k\)(i ^ (1 << j))的状态转移。但是这里的转移有点不一样,对于 \(j\),需要二分在 \(f_k\) 以后其最多能买几个物品,具体来说,还需要维护商品价格的前缀和来进行二分。
统计答案也有点不一样,枚举每个状态 \(i\),如果 \(f_i=n\),也就是可以买完所有物品,那么就用除 \(i\) 外其余硬币的价值来更新 \(ans\)。
时间复杂度 \(O(n2^n)\)。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 17;
const int M = 1e5 + 5;
const int INF = 1e16;
int n, m, a[M], b[M], f1[1 << N], f2[1 << N], sum[M];
int find(int l, int x) {
int t = l, r = m, mid, ans = 0;
while (l <= r) {
mid = l + r >> 1;
if (sum[mid] - sum[t - 1] <= x) ans = mid, l = mid + 1;
else r = mid - 1;
}
return ans;
}
signed main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= m; i++)
cin >> b[i], sum[i] = sum[i - 1] + b[i];
for (int i = 0; i < (1 << n); i++) {
for (int j = 1; j <= n; j++) {
if (!(i & (1 << j - 1))) continue;
f1[i] += a[j];
f2[i] = max(f2[i], find(f2[i ^ (1 << j - 1)] + 1, a[j]));
}
}
int ans = INF, cnt = 0;
for (int i = 1; i <= n; i++) cnt += a[i];
for (int i = 0; i < (1 << n); i++)
if (f2[i] == m) ans = min(ans, f1[i]);
cout << (ans == INF ? -1 : (cnt - ans)) << "\n";
return 0;
}
同样是需要换个思路,挺巧妙的。\(f_{i,j}\) 表示前 \(i\) 位匹配情况为 \(j\) 的方案数。需要预处理出 \(vis_{i,j}\) 表示第 \(i\) 位字符 \(j\) 的匹配情况。转移时需要主动转移:用 \(f_{i,j}\) 来更新 \(T\) 加上字符 \(k\) 后的情况 f[i + 1][j & vis[i + 1][k]],也就是之前就匹配的与第 \(i+1\) 为能匹配的交集。
最后统计答案的时候是枚举 \(j\),如果其恰好有 \(k\) 个串能匹配就累加答案,时间复杂度 \(O(km2^n)\),其中 \(m\) 为字符串的长度,\(k=26\)
。
#include <bits/stdc++.h>
using namespace std;
const int N = 15;
const int M = 55;
const int Mod = 1000003;
string s[M];
int f[M][(1 << N) + 1], vis[M][M];
inline int cal(int x) {
int res = 0;
while (x) res += (x & 1), x >>= 1;
return res;
}
int main() {
int T; cin >> T;
while (T--) {
memset(f, 0, sizeof(f));
memset(vis, 0, sizeof(vis));
int n, k, len; cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> s[i];
len = s[1].size(), f[0][(1 << n) - 1] = 1;
for (int i = 1; i <= len; i++)
for (int j = 1; j <= 26; j++)
for (int k = 1; k <= n; k++)
if (s[k][i - 1] == '?' || s[k][i - 1] == (j + 'a' - 1))
vis[i][j] |= (1 << k - 1);
for (int i = 0; i < len; i++)
for (int j = 0; j < (1 << n); j++)
for (int k = 1; k <= 26; k++)
f[i + 1][j & vis[i + 1][k]] = (f[i + 1][j & vis[i + 1][k]] + f[i][j]) % Mod;
int ans = 0;
for (int i = 0; i < (1 << n); i++)
if (cal(i) == k) ans = (ans + f[len][i]) % Mod;
cout << ans << "\n";
}
return 0;
}
状压+概率 dp。思路和题解有些不一样,但感觉更好想。\(f_i\) 表示吃掉的鱼为 \(i\) 的概率数,转移就可以比较自然地主动转移:记 \(cnt\) 表示 \(i\) 中 \(1\) 的个数,那么每次枚举不在 \(i\) 中的两条鱼 \(j,k\),按 \(j\) 吃掉 \(k\) 转移(无视顺序,因为枚举时会枚举两遍),\(f_{i|2^k}\leftarrow^+\frac{f_i\times p_{j,k}\times2}{(n-cnt)\times(n-cnt-1)}\)。
还有一种状态表示的方法是记 \(f_i\) 表示剩余的鱼是 \(i\) 的概率,那么对应的就是被动转移。
\(ans_i=f_{k}\),其中除 \(i\) 外的所有鱼都在 \(k\) 中,时间复杂度 \(O(n^22^n)\)。
#include <bits/stdc++.h>
using namespace std;
const int N = 18;
double f[1 << N], p[N][N], fac[N];
int main() {
int n; cin >> n;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cin >> p[i][j];
fac[0] = 1;
for (int i = 1; i <= n; i++) fac[i] = fac[i - 1] * i;
f[0] = 1;
for (int i = 0; i < (1 << n); i++) {
int cnt = 0;
for (int j = 0; j < n; j++)
if (i & (1 << j)) cnt++;
for (int j = 0; j < n; j++) {
if (i & (1 << j)) continue;
for (int k = 0; k < n; k++)
if (!(i & (1 << k)) && (j != k))
f[i | (1 << j)] += f[i] * p[k][j] / (n - cnt) / (n - cnt - 1) * 2;
}
}
for (int i = 0; i < n; i++)
printf("%.6f ", f[((1 << n) - 1) ^ (1 << i)]);
return 0;
}
由数据范围得出只能对 \(m\) 进行状压。\(f_i\) 表示 \(i\) 中的团体已经站好的出列的最少偶像(不只是存在于 \(i\) 中的团体要出列)。它们之间的顺序是什么?其实这并不重要,或者说可以通过一些手段让顺序变得不重要。
我们枚举每个团体 \(j\) 来转移,每次假设把 \(j\) 放在最后面,为了方面算位置,需预处理 \(s_{i,j}\) 表示前 \(i\) 个人种团队 \(j\) 的人数,团队 \(j\) 的总人数就是 \(s_{n,j}\),同时 \(cnt_i\) 等于 \(i\) 中所有团队的人数和。这样,就是把 \(j\) 的人放在 \([cnt_i-s_{n,j}+1,cnt_i]\) 中,于是要移动的人数就是 \(s_{n,j}-(s_{cnt_i}-s_{cnt_i-s_{n,j}})\)。那么转移就是去掉 \(j\) 的状态(i ^ (1 << j))加上移动人数的最小值。
这样其实就可以忽略顺序了,因为每个团体在后面都会被更新,且必有一个团体在最后,而对于其它的团体,顺序已经不重要了,因为我们关心的是他们的总人数。
由于是取 \(\min\),记得把初值赋为最大值,\(f_0=0\)。时间复杂度:\(O(m2^m)\)。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
const int M = 20;
int s[N][M], f[1 << M];
int main() {
int n, m; cin >> n >> m;
for (int i = 1; i <= n; i++) {
int x; cin >> x; x--;
for (int j = 0; j < m; j++)
s[i][j] = s[i - 1][j];
s[i][x]++;
}
memset(f, 0x3f, sizeof(f));
f[0] = 0;
for (int i = 1; i < (1 << m); i++) {
int cnt = 0;
for (int j = 0; j < m; j++)
if (i & (1 << j)) cnt += s[n][j];
for (int j = 0; j < m; j++)
if (i & (1 << j))
f[i] = min(f[i], f[i ^ (1 << j)] + s[n][j] - (s[cnt][j] - s[cnt - s[n][j]][j]));
}
cout << f[(1 << m) - 1] << "\n";
return 0;
}
一道卡常状压。乍一眼思路很明显:记 \(f_i\) 为用了 \(i\) 的卡片的方案数(若 \(i\) 为厄运数字则为 \(0\)),转移也很显然,枚举每个 \(i\) 中有的 \(j\) ,累加 \(i\) 去掉 \(j\) 的状态的方案数。初始 \(f_0=1\)。
但是正常 \(O(n2^n)\) 的复杂度卡得有点紧,这时,就需要一点卡常了。在枚举 \(j\) 这个环节,正常是要 \(n\) 个卡片枚举过去,实际上,其实只要枚举 \(i\) 中有的就行了。这里涉及到一个技巧:那就是每次取出 lowbit(i),就能取出所有为 1 的位。
事实上其实复杂度没有变,但 \(O(n)\) 的部分却跑不满,如果还是超一点的话可以尝试开一下 O2。
#include <bits/stdc++.h>
using namespace std;
const int N = 24;
const int Mod = 1e9 + 7;
int a[N], f[1 << N], b[N], dis[1 << N];
inline void work(int x) {
for (int i = x; i; i -= i & -i) {
f[x] += f[x ^ (i & (-i))];
if (f[x] > Mod) f[x] -= Mod;
}
}
int main() {
int n; cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i], dis[1 << i - 1] = a[i];
int m; cin >> m;
for (int i = 1; i <= m; i++) cin >> b[i];
f[0] = 1;
for (int i = 0; i < (1 << n); i++) {
dis[i] = dis[i ^ (i & -i)] + dis[i & (-i)];
if (dis[i] != b[1] && dis[i] != b[2]) work(i);
}
cout << f[(1 << n) - 1];
return 0;
}
一道重点不在状压、但用到了一个实用技巧的题。设 \(f_{i,j}\) 表示在前 \(i\) 层已经安排好了 \(j\) 的最小花费,转移是枚举 \(k\) 表示第 \(i\) 行安排什么(不能有冲突),并从 \(i-1\) 层转移,这个思路不是难点,难点在于处理。
理清一下,需要维护一下几个量:
- \(s_{i,j}\) 表示第 \(i\) 个地铁安排在第 \(j\) 层的花费
- \(vis_{i,j}\) 表示 \(i,j\) 地铁是否能安排在同一层,这里需要用双指针做到 \(O(n^2m)\),但事实证明 \(O(n^2m^2)\) 剪枝一下也能过
- \(g_{i,j}\) 表示第 \(i\) 层安排 \(j\) 状态的花费,需要判断是否有冲突,没有的话直接枚举累加 \(s\),复杂度 \(O(n^32^n)\)
接下来可以列出一个式子:\(f_{i,j}=\min\{f_{i-1,j\oplus k}+g_{i,k}\}\),普通转移是 \(O(n2^{2n})\),无法通过,于是考虑优化:
发现在处理 \(k\) 是 \(j\) 的子集上花了许多时间,涉及到了一个技巧,可以通过一下代码较快实现某一集合子集的枚举:
for (int k = j; k; k = (k - 1) & j)
//do something
答案就是 \(f_{n,2^n-1}\),可以证明复杂度是 \(O(m+3^nn)\) 的。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 15;
const int M = 1e5 + 5;
inline int read() {
int w = 1, q = 0; char ch = ' ';
while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if (ch == '-') w = -1, ch = getchar();
while (ch >= '0' && ch <= '9') q = q * 10 + ch - '0', ch = getchar();
return w * q;
}
int a[N][M], cnt[N], b[N][M], s[N][M], sum[N][1 << N], f[N][1 << N];
bool vis[N][N];
signed main() {
int n = read(), m = read();
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
a[i][j] = read();
for (int i = 1; i <= n; i++) {
cnt[i] = read();
for (int j = 1; j <= cnt[i]; j++)
b[i][j] = read();
sort(b[i] + 1, b[i] + 1 + cnt[i]);
for (int j = 1; j <= n; j++)
for (int k = 1; k <= cnt[i]; k++)
s[i][j] += a[j][b[i][k]];
}
for (int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++)
for (int k = 1, p = 0; k <= cnt[i]; k++) {
while (b[j][p + 1] <= b[i][k] && p < cnt[j]) p++;
if (b[j][p] == b[i][k]) {
vis[i][j] = vis[j][i] = 1;
break;
}
}
memset(sum, 0x3f, sizeof(sum));
for (int i = 1; i <= n; i++)
for (int j = 0; j < (1ll << n); j++) {
sum[i][j] = 0;
for (int k = 1; k <= n && sum[i][j] != sum[0][0]; k++) {
if (!(j & (1ll << k - 1))) continue;
for (int t = 1; t <= n; t++)
if ((j & (1ll << t - 1)) && vis[k][t]) {
sum[i][j] = sum[0][0];
break;
}
if (sum[i][j] != sum[0][0]) sum[i][j] += s[k][i];
}
}
for (int j = 0; j < (1ll << n); j++)
f[1][j] = sum[1][j];
for (int i = 2; i <= n; i++)
for (int j = 0; j < (1ll << n); j++) {
f[i][j] = f[i - 1][j];
for (int t = j; t; t = (t - 1) & j)
f[i][j] = min(f[i][j], f[i - 1][j ^ t] + sum[i][t]);
}
cout << f[n][(1 << n) - 1] << '\n';
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号