jiffies相关时间比较函数time_after、time_before详解
1. jiffies简介
首先，操作系统有个系统专用定时器(system timer)，俗称滴答定时器，或者系统心跳。
全局变量jiffies取值为自操作系统启动以来的时钟滴答的数目，数据类型为 unsigned long volatile (32位无符号长整型)，最大取值是2^32-1。
2. jiffies与秒的转换
将 jiffies转换为秒，可采用公式：(jiffies/HZ) 计算。
将 秒转换为jiffies，可采用公式：(seconds*HZ) 计算。
示例(本博客后面将介绍涉及到的time_before)：
unsgned long delay = jiffies + 2*HZ;
while(time_before(jiffies, delay)); // 忙等待两秒，占用CPU的一个核心，期间不执行调度
3. jiffies的溢出介绍
当时钟中断发生时，jiffies值就加1。
假定HZ=100，那么1个jiffies等于1/100 秒，jiffies可记录的最大秒数为(2^32 -1)/100=42949672.95秒，约合497天或1.38年，
当取值到达最大值时仍继续加1，就变为了0！
即HZ=100时，连续累加的溢出时间是一年又四个多月，如果程序对jiffies的溢出没有加以充分考虑，那么在连续运行一年又四个多月后，这些程序还能够稳定运行吗？
4. 示例1，一个 jiffies溢出造成程序逻辑出错 的示例
unsigned long timeout = jiffies + HZ/2; /* timeout in 0.5s */
/* do some work ... */
do_somework();
/* then see whether we took too long */
if (timeout > jiffies) {
/* we did not time out, call no_timeout_handler() ... */
no_timeout_handler();
} else {
/* we timed out, call timeout_handler() ... */
timeout_handler();
}
本例的意图：
从当前时间起，如果在0.5秒内执行完do_somework()，则调用no_timeout_handler()。如果在0.5秒后执行完do_somework()，则调用timeout_handler()。
然后当溢出时呢？ 该意图会被打破吗？
假设程序开始执行前，timeout值已经接近最大值(即2^32-1 ) ，jiffies的值是(timeout-HZ/2)，
之后do_some_work执行了挺久(超过0.5秒)，jiffies的值也发生了溢出(jiffies做自增操作的中途超过了32位无符号数的最大值)，
溢出后的值，可能是很小的一个数字，所以造成jiffies的值 < timeout,
之后的代码执行流就走到了no_time_handler()这里，这显然和程序设计者的初衷(意图)是违背的。
5. Linux内核如何来防止jiffies溢出
Linux内核中提供了一些宏，可有效地解决由于jiffies溢出而造成程序逻辑出错的情况。
PS：下图源自Linux Kernel version 3.10.14
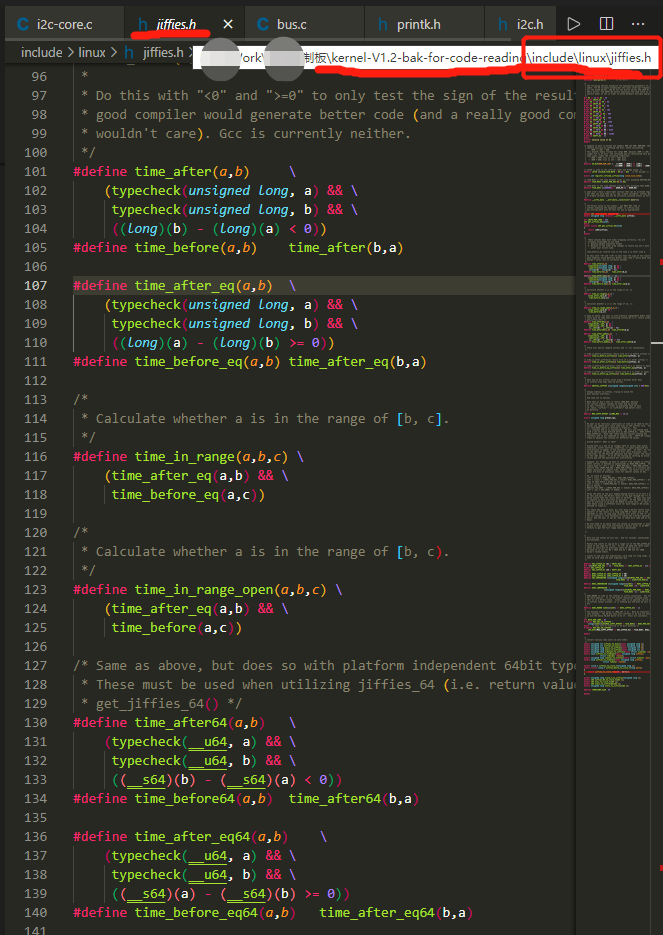
同时根据 #define time_before(a,b) time_after(b,a) ，我们可以知道
* time_before(a,b) returns true if the time b is after time a.
6. time_after 在驱动代码中的应用展示
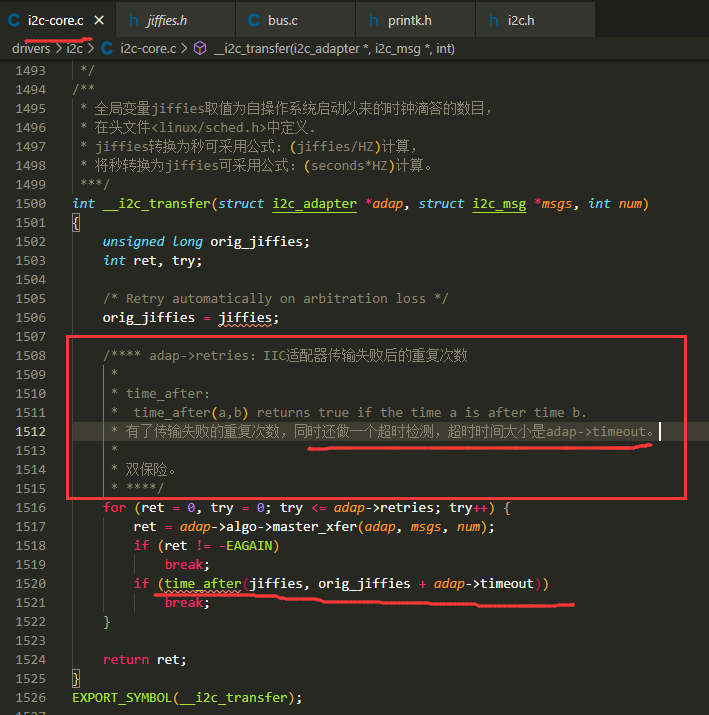
7. time_after等用于时间比较的宏的原理简介
下面的文字摘录自博文：https://blog.csdn.net/jk110333/article/details/8177285
读者先大致浏览一遍即可，不必纠结于绞尽脑汁的细节理解, 后面我将表达个人理解，读者也可以直接向下浏览，看我的个人理解。
/**********************************开始摘录********************************************/
我们仍然以8位无符号整型(unsigned char)为例来加以说明。仿照上面的time_after宏，我们可以给出简化的8位无符号整型对应的after宏：
#define uc_after(a, b) ((char)(b) - (char)(a) < 0)
设a和b的数据类型为unsigned char，b为临近8位无符号整型最大值附近的一个固定值254，下面给出随着a（设其初始值为254）变化而得到的计算值：
a b (char)(b) - (char)(a)
254 254 0
255 - 1
0 - 2
1 - 3
...
124 -126
125 -127
126 -128
127 127
128 126
...
252 2
253 1
从上面的计算可以看出，设定b不变，随着a（设其初始值为254）不断增长1，a的取值变化为：
254, 255, (一次产生溢出)
0, 1, ..., 124, 125, 126, 127, 126, ..., 253, 254, 255, (二次产生溢出)
0, 1, ...
...
而(char)(b) - (char)(a)的变化为：
0, -1,
-2, -3, ..., -126, -127, -128, 127, 126, ..., 1, 0, -1,
-2, -3, ...
...
从上面的详细过程可以看出，当a取值为254，255, 接着在（一次产生溢出）之后变为0，然后增长到127之前，uc_after(a,b)的结果都显示a是在b之后，这也与我们的预期相符。但在a取值为 127之后， uc_after(a,b)的结果却显示a是在b之前。
从上面的运算过程可以得出以下结论：
使用uc_after(a,b)宏来计算两个8位无符号整型a和b之间的大小（或先/后，before/after），那么a和b的取值应当满足以下限定条件：
. 两个值之间相差从逻辑值来讲应小于有符号整型的最大值。
. 对于8位无符号整型，两个值之间相差从逻辑值来讲应小于128。
从上面可以类推出以下结论：
对于time_after等比较jiffies先/后的宏，两个值的取值应当满足以下限定条件：
两个值之间相差从逻辑值来讲应小于有符号整型的最大值。
对于32位无符号整型，两个值之间相差从逻辑值来讲应小于2147483647。
对于HZ=100，那么两个时间值之间相差不应当超过2147483647/100秒 = 0.69年 = 248.5天。
对于HZ=60，那么两个时间值之间相差不应当超过2147483647/60秒 = 1.135年。
在实际代码应用中，需要比较的先/后的两个时间值之间一般都相差很小，范围大致在1秒~1天左右，所以以上time_after等比较时间先 /后的宏完全可以放心地用于实际的代码中。
/***********************************摘录结束******************************************/
看完这段文字，感觉有点绕的，那么原理到底是啥呢？ 是一堆数学计算吗？是啊 ，就是这数学规律！
凡事都是有利有弊的，针对一件事物的优化，有利处，必然带来不利之处，从哲学角度来进行理解，事物的两面性。
本文第4部分，示例1介绍了jiffies的一个例子，它的弊处是会溢出，如果我们不抓住溢出这个弊处来看待这件事物，那么timeout的值可以做的很大，这是优势。
然而溢出是真实存在的，无法满足客观需求的，所以需要改进，
从该数学规律入手进行改进后，不溢出了，这是优势，
但是改进后对timeout的值也缩小了使用范围，这是为了达到该优势所带来的必要开销或损耗。这就是事物的两面性。
8. 示例2，对示例1进行改进：使用time_before宏后的正确代码
unsigned long timeout = jiffies + HZ/2; /* timeout in 0.5s */
/* do some work ... */
do_somework();
/* then see whether we took too long */
if (time_before(jiffies, timeout)) {
/* we did not time out, call no_timeout_handler() ... */
no_timeout_handler();
} else {
/* we timed out, call timeout_handler() ... */
timeout_handler();
}
.
