斜率优化总结

例题引入

题目：Luogu P2365 任务安排
题解：题解 P2365 【任务安排】

模板总结

对于此类方程：\(F[i]={min_{L(i) \leq j \leq R(i)}} \begin{Bmatrix} F[j]+val(i,j) \end{Bmatrix}\)
暂时忽略min和范围得：\(F[i]=F[j]+val(i,j)\)
整理得：\(F[j]=-val(i,j)+F[i]\)
令\(-val(i,j)=f(i)*g(j)+h(i)\)
则\(F[j]=f(i)*g(j)+F[i]+h(i)\)
注意到对于每个确定的 \(i\) ，其 \(f(i)\) 和 \(h(i)\) 值确定，即可看成常量，因此可以把 \(F[j]\) 看作 \(y\) ，把 \(f(i)\) 看作 \(a\) ，把 \(g(j)\) 看作 \(x\) ，把 \(F[i]+h(i)\) 看作 \(b\) ，则每一个决策可转化成求一个过点 \((x,y)\) 的斜率已确定为 \(a\) 的直线 \(y=ax+b\) 的最小的截距 \(b\) ，也就求出了最小的 \(F[i]\) 。
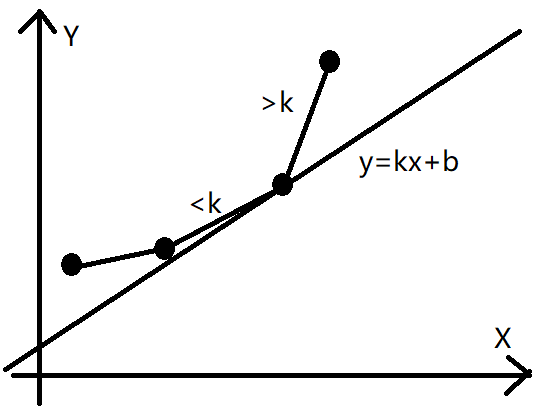
考虑其几何意义，如图，可以维护一个决策点的“下凸壳”，易知当直线的斜率处于下凸壳的两条相邻线段之间时决策最优。

---

一些坑

• \(g(j)\) 不单调
• 有些情况下（比如 \(j\) 的范围有限制）无法用单调队列维护
• 分母为0
• 浮点数存在精度问题

---

参考资料

• 李煜东《算法竞赛进阶指南》
• Luogu @威慑