数据结构详解
1 using System; 2 using System.Collections.Generic; 3 using System.Linq; 4 using System.Text; 5 using System.Threading.Tasks; 6 7 namespace ConsoleApp1 8 { 9 /// <summary> 10 /// O(1)常数阶 < O(logn)对数阶 < O(n)线性阶 < O(n~2)平方阶 < O(n~3)(立方阶) < O(2~n) (指数阶) 11 /// 由数学函数可知时间复杂度描述的是算法的执行次数随元素个数的增长幅度 12 /// </summary> 13 class Program 14 { 15 //时间复杂度: 16 //先分别计算程序中每条语句的执行次数,然后用总的执行次数间接表示程序的运行时间, 17 //一个算法所编程序运行时间的多少,用的并不是准确值(事实上也无法得出),而是根据合理方法得到的预估值, 18 //即时间复杂度描述的是算法的执行次数随元素个数的增长幅度。 19 //对于一个算法(或者一段程序)来说,其最简频度往往就是最深层次的循环结构中某一条语句的执行次数, 20 //例如2n+1当n无穷大时化简为n,实际上就是a++语句的执行次数O(n);同样2n~2+2n+1当n无穷大时简化为n~2,实际上就是最内层循环中num++语句的执行次数O(n~2)。 21 //用无穷大的思想去理解时间复杂度的表示方法。 22 23 //空间复杂度: 24 //和时间复杂度类似,一个算法的空间复杂度,也常用大O记法表示。 25 //要知道每一个算法所编写的程序,运行过程中都需要占用大小不等的存储空间,例如: 26 //程序代码本身所占用的存储空间; 27 //程序中如果需要输入输出数据,也会占用一定的存储空间; 28 //程序在运行过程中,可能还需要临时申请更多的存储空间。 29 //程序自身所占用的存储空间取决于其包含的代码量,如果要压缩这部分存储空间,就要求我们在实现功能的同时,尽可能编写足够短的代码。 30 //程序运行过程中输入输出的数据,往往由要解决的问题而定,即便所用算法不同,程序输入输出所占用的存储空间也是相近的。 31 //事实上,对算法的空间复杂度影响最大的,往往是程序运行过程中所申请的临时存储空间。不同的算法所编写出的程序,其运行时申请的临时存储空间通常会有较大不同。 32 //如果随着输入值n的增大,程序申请的临时空间成线性增长,则程序的空间复杂度用O(n)表示。 33 //如果随着输入值n的增大,程序申请的临时空间成n2关系增长,则程序的空间复杂度用O(n2)表示。 34 35 //数据结构: 36 //数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。 37 //数据结构分为逻辑结构(树型一对多关系(二叉树、平衡二叉树AVL、红黑树、B树、B+树等)、图型多对多关系)和存储结构(线型一对一(顺序(数组)、链接(单链表、双链表、循环链表)、索引(栈、队列)、散列即键值(字典)))。 38 //特别提示千万不要以为数组这种结构是内存直接存在的,内存直接存在的只有变量和指针,所以数组也是SDK帮我们实现的一种用来存储数据的逻辑结构,可以尝试自己实现一下单链表。 39 //存储结构是根据元素在内存中的相对位置(内存变量)和地址指针封装成的一种结构, 40 //逻辑结构是利用存储结构和内存变量值封装成的具有逻辑关系的数据结构。 41 //可以自己研究一下SDK框架带的各种集合(如List<T>、ArrayList<T>、LinkedList<T>)是使用什么数据结构实现的分装。 42 43 static void Main(string[] args) 44 { 45 int[] arr = new int[10] { 5,2,1,4,8,3,12,55,31,16}; 46 int[] tt = heapSort(arr); 47 } 48 49 #region 冒泡排序 O(n)-O(n~2) 稳定(如果两个元素相等次序不会改变) 50 static int[] bubbleSort(int[] arr) 51 { 52 var len = arr.Length; 53 for (var i = 0; i < len - 1; i++) 54 { 55 for (var j = 0; j < len - 1 - i; j++) 56 { 57 if (arr[j] > arr[j + 1]) 58 { // 相邻元素两两对比 59 var temp = arr[j + 1]; // 元素交换 60 arr[j + 1] = arr[j]; 61 arr[j] = temp; 62 } 63 } 64 } 65 return arr; 66 } 67 #endregion 68 69 #region 堆排序 O(nlogN)-O(nlogN) 底数根据切分值而定,这里为2分法,不稳定(如果两个元素相等次序可能会改变) 70 //堆排序是指利用堆这种数据逻辑结构思想所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是全部小于(或者全部大于)它的父节点。 71 static void buildMaxHeap(int[] arr,int len) 72 { // 建立大顶堆 73 for (int i = (int)Math.Floor((decimal)len / 2); i >= 0; i--) 74 { 75 heapify(arr, i, len); 76 } 77 } 78 79 static void heapify(int[] arr, int i,int len) 80 { // 堆调整 81 var left = 2 * i + 1; 82 var right = 2 * i + 2; 83 var largest = i; 84 if (left < len && arr[left] > arr[largest]) 85 { 86 largest = left; 87 } 88 if (right < len && arr[right] > arr[largest]) 89 { 90 largest = right; 91 } 92 if (largest != i) 93 { 94 swap(arr, i, largest); 95 heapify(arr, largest, len); 96 } 97 } 98 99 static void swap(int[] arr, int i, int j) 100 { 101 var temp = arr[i]; 102 arr[i] = arr[j]; 103 arr[j] = temp; 104 } 105 106 static int[] heapSort(int[] arr) 107 { 108 int len = arr.Length; 109 110 //先将数组转为大顶堆结构 111 buildMaxHeap(arr, len); 112 113 //接下来对堆结构arr进行排序 114 for (var i = arr.Length - 1; i > 0; i--) 115 { 116 swap(arr, 0, i); //每次生成大顶堆后,把堆顶的最大元素值放到数组的最后,然后一次执行后面的元素,每执行一次大顶堆即可找出一个最大值 117 heapify(arr, 0, i); 118 } 119 120 return arr; 121 } 122 #endregion 123 } 124 }
冒泡排序示意图:
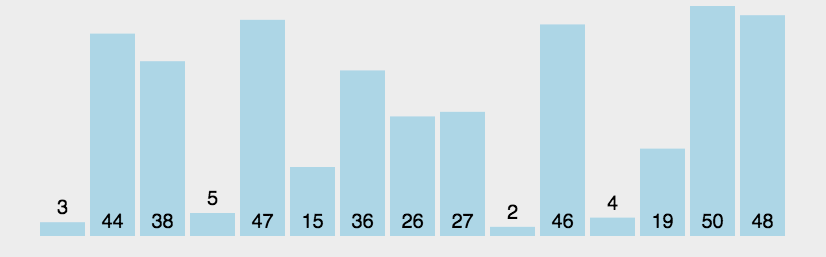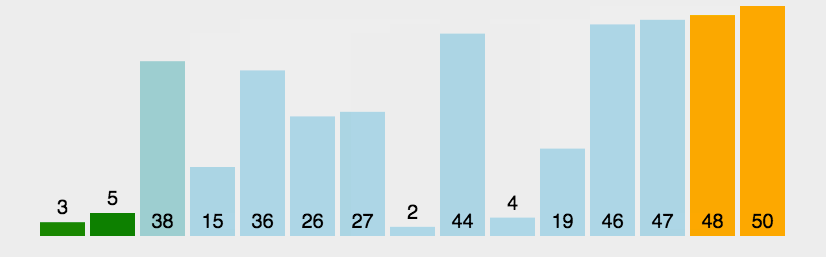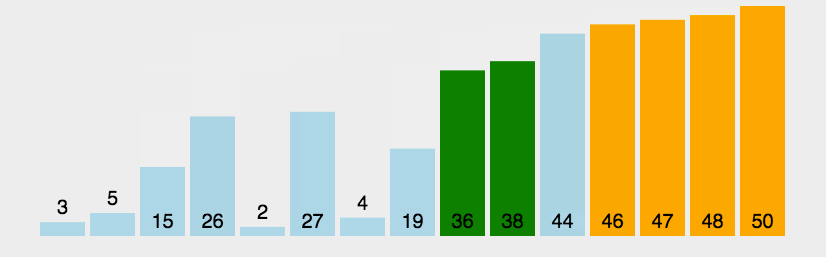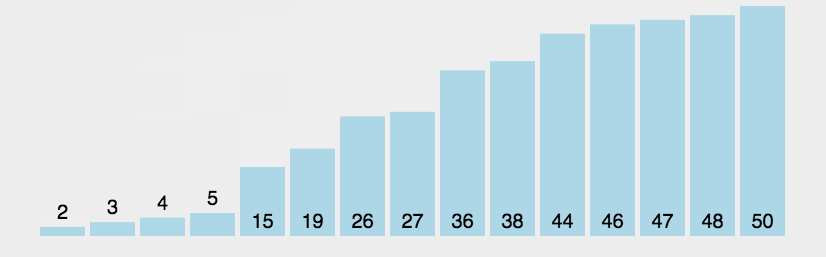
堆排序示意图:

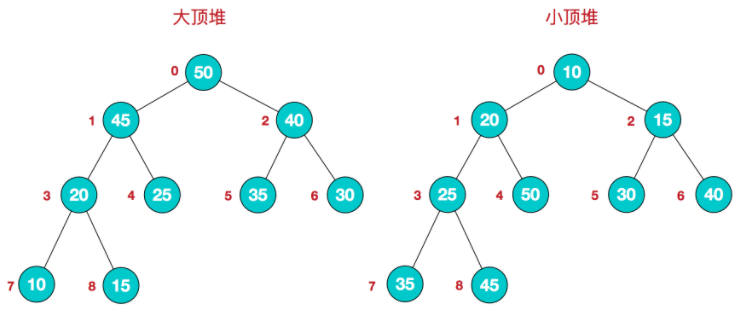
堆结构示意图: