最后之作-Last Order(bushi
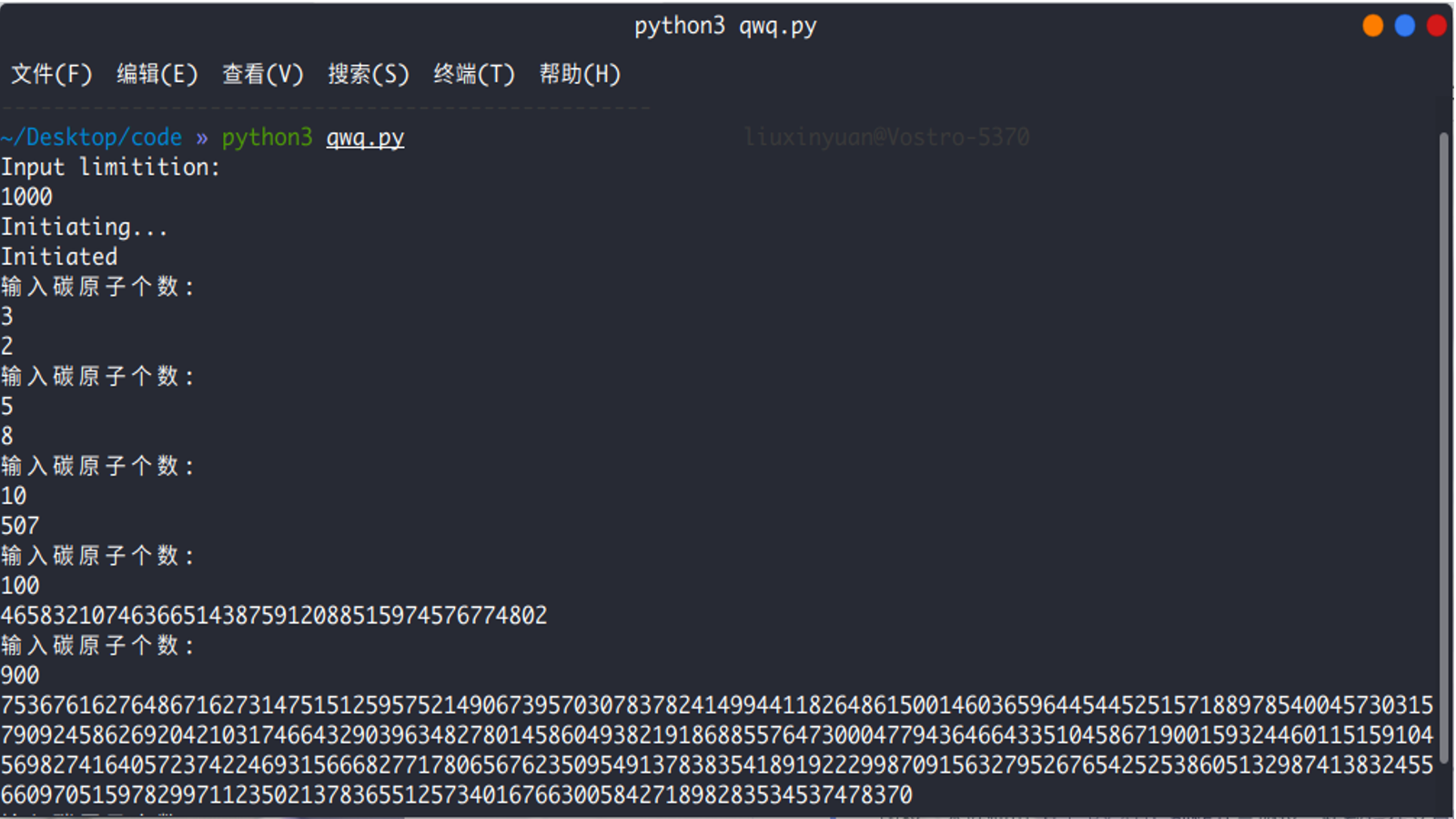
最近化学学有机选修,讲羧酸的时候我想到一个问题:不考虑空间异构、能否稳定存在等问题,某高级饱和脂肪酸有多少种同分异构体?做为一名退役的OIer,我将它抽象为了另一个问题:含\(n\)个\(C\)的饱和链烃基有多少同分异构体?在我废寝忘食(不写作业)研究了\(n(n\geq 20)\)天,经历了无数失败后,我终于写出了下面的代码。目前计算前\(1000\)个结果的时间小于\(1s\)(应该没有人丧心病狂到想知道一千烷基的同分异构体数量吧……),具体原理抽空放上来qwq
f = []
g = []
f.append(1)
g.append(1)
print("Input limitition:")
len = int(input())
print("Initiating...")
for i in range(1, len):
if ((i - 1) % 3 == 0):
f.append(2 * f[(i - 1) // 3])
else:
f.append(0)
for j in range(0, i, 2):
f[i] = f[i] + 3 * f[j // 2] * f[i - 1 - j]
for j in range(0, i):
f[i] = f[i] + g[j] * f[i - 1 - j]
f[i] = f[i] // 6
g.append(0)
for j in range(0, i + 1):
g[i] = g[i] + f[j] * f[i - j]
print("Initiated")
while 1:#什么?你想退出?你都会用Python了你不会退出?
print("输入碳原子个数:")
n = int(input())
print(f[n])


 浙公网安备 33010602011771号
浙公网安备 33010602011771号