结对项目
| 软件工程 | 点我 |
|---|---|
| 作业要求 | 点我 |
| 作业目标 | 熟悉如何结对开发项目 |
Github与合作者
合作者(学号):
- 王欢:3218005443
- 孔止:3118005414
Github链接:
https://github.com/Holy-Acile/Pair-program
Github目录结构:
document #设计文档
|-- 需求分析文档.md
|-- 模块设计文档.md
module #模块
|-- unit_test #模块单元测试
|-- *.py #模块代码
performance #性能分析
|-- before #改进前
|-- *.txt #line_profiler性能分析
|-- *.png #实际运行时间
|-- after #改进后
|-- test.py #性能分析测试代码
Myapp.py #主程序
Exercises.txt #生成的题目
Answers.txt #题目的答案
PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时 (分钟) |
实际耗时 (分钟) |
|---|---|---|---|
| Planning | 计划 | 60 | 120 |
| · Estimate | · 估计这个任务需要多少时间 | 60 | 120 |
| Development | 开发 | 810 | 1160 |
| · Analysis | · 需求分析 (包括学习新技术) | 120 | 180 |
| · Design Spec | · 生成设计文档 | 120 | 180 |
| · Design Review | · 设计复审 | 60 | 60 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | 60 |
| · Design | · 具体设计 | 120 | 240 |
| · Coding | · 具体编码 | 200 | 260 |
| · Code Review | · 代码复审 | 100 | 60 |
| · Test | · 测试 (自我测试,修改代码,提交修改) | 60 | 120 |
| Reporting | 报告 | 120 | 210 |
| · Test Repor | · 测试报告 | 60 | 120 |
| · Size Measurement | · 计算工作量 | 30 | 30 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 60 |
| · 合计 | 990 | 1490 |
设计实现过程
共有8个模块,每个模块的功能如下:
Myapp:用于输入输出的对接,按照格式处理生成的题目和答案;
gen_problem_list:生成题目集。
先调用gen_problem生成题目,然后把生成的题目格式化为字符串(注意有些分数要用带分数表示),且使题目之间不重复
gen_problem:生成一个包含数字和符号的题目
gen_num:生成一个随机分数
check_problem:检查题目是否重复
cal_problem_list:计算题目集的答案。
先把题目的字符串转化为数字+符号的题目,然后交给cal_problem处理,计算出结果
cal_problem:计算一个题目的答案
check_txt(附加题):对比已知题目和答案
模块调用图
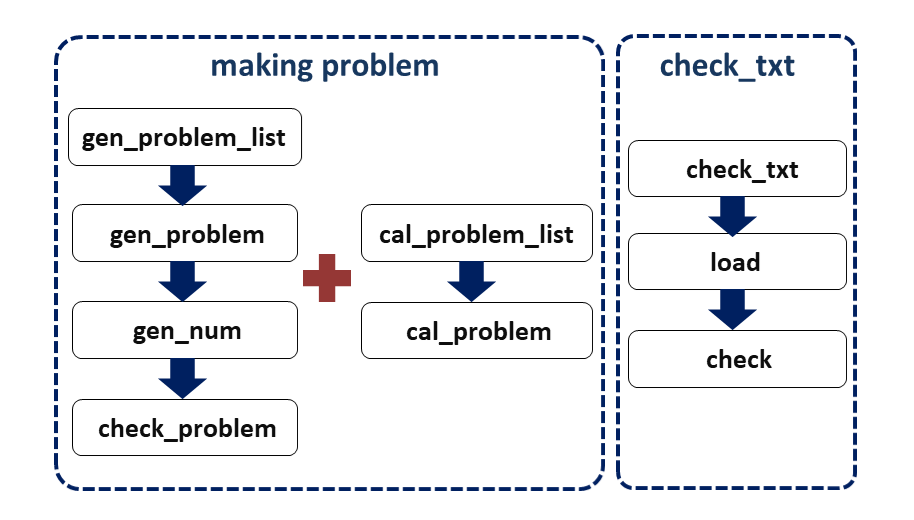
代码说明
关键性代码,生成问题:gen_problem.py,计算问题:cal_problem
代码一
from module.gen_num import gen_num
import random
#生成题目
def gen_problem(mod):
problem = []
const_op = ("+", "-", "×", "÷")
ok = False
while ok == False :
ok = True
#生成运算符
cnt_op = random.randint(1, 3)
op_list = []
while cnt_op:
bit = random.randint(0, 3)
op_list.append(const_op[bit])
cnt_op -= 1
num = gen_num(mod)
problem = [num]
last_op = " "
for op in op_list:
part_num = gen_num(mod)
#交换标记,决定problem(值为num)和part_num的位置
swap_flag = random.randint(0, 1)
t = 0 #num和part_num的运算结果
#加
if op == "+":
t = num + part_num
#减
elif op == "-":
#对problem和part_num的位置进行分类
if swap_flag == 0 or num >= mod:
swap_flag = 0
t = num - part_num
while t < 0:
part_num = gen_num(min(mod, int(num)))
t = num - part_num
else:
t = part_num - num
while t < 0:
part_num = gen_num(int(mod - num)) + num
t = part_num - num
if mod > 5 and part_num.denominator > mod :
ok = False
break
#乘
elif op == "×":
t = num * part_num
#除
else:
#对problem和part_num的位置进行分类
if swap_flag == 0:
while part_num == 0:
part_num = gen_num(mod)
t = num / part_num
else:
if num == 0:
swap_flag = 0
while part_num == 0:
part_num = gen_num(mod)
t = num / part_num
else:
t = part_num / num
#加括号
bracket_flag = False
if op == "×" or op == "÷":
if last_op == "+" or last_op == "-":
bracket_flag = True
if bracket_flag:
problem = ["("] + problem + [")"]
#交换位置
if swap_flag == 1:
if bracket_flag == False and last_op != " ":
problem = ["("] + problem + [")"]
problem = [part_num] + [op] + problem
else:
problem = problem + [op] + [part_num]
num = t
last_op = op
if mod <= 5 and num == 0 : ok = False
return problem
思路
因为一个问题,其实就是一个算术表达式。所以,我们只要构造出符合条件的算术表达式就可以了。这里采用了增量构造表达式的方法,方法如下:
- 假设当前的表达式为
problem - 这时,随机生成一个数
part_num,和一个操作符op - 接着,我们可以由此生成新的表达式,这个表达式为:
(problem) + op + part_num,或者:part_num + op + (problem) - 新的表达式又可以作为
problem,执行第2步
代码整体思路:
- 预处理出要生成什么运算符
- 初始化表达式
problem,设置变量num。num的含义为:表达式problem的值 - 进入增量构造表达式的循环
- 生成
part_num - 设置标记变量
swap_flag,作用:决定problem和part_num的相对位置 - 根据
num,part_num和swap_flag计算出目标表达式的值 - 设置标记变量
bracket_flag,作用:决定problem是否有必要加括号 - 根据标记变量,
part_num和运算符op,生成目标表达式,然后再赋值给problem
代码二
import re
from fractions import Fraction
# 计算单个题目
def cal_problem(input_pro):
t1 = "'" # 先处理假分数
if (t1 in input_pro):
input_pro = re.sub(r"(\d+'\d+/\d+)", r'(\1)', input_pro)
input_pro = input_pro.replace("'", '+')
input_pro = re.sub(r'(\d+/\d+)', r'(\1)', input_pro) # 将再将分数优先处理
t2 = "÷"
if (t2 in input_pro):
input_pro = input_pro.replace("÷", '/')
t3 = "×"
if (t3 in input_pro):
input_pro = input_pro.replace("×", '*')
transformed_pro = re.sub(r'(\d+)', r'Fraction("\1")', input_pro) # 小数转分数
res_int = int(eval(input_pro))
res_fra = eval(transformed_pro) - res_int
if (res_fra != 0 and res_int != 0):
res = str(res_int) + "'" + str(res_fra) # 返回分数
else:
res = str(eval(transformed_pro)) # 返回整数字符化
return res # 返回一个字符串形式的参数可能为整数,可能为真分数
思路
由于引入的问题表达式以为字符串传入,故需要对计算符号等进行处理,此处采用了正则表达式中符号替换结合eval函数对字符串表达式计算的方法,整体思路如下:
- 优先级处理:由于分数中的表达式与计算时除号相同,为避免冲突,需要将分数部分进行加括号,故而利用正则表达式替换为表达式中的分数加括号
- 符号替换:乘号除号替换为计算符号*和/,真分数包含‘的要替换为加号
- 计算结果处理,将计算后的假分数转为标准的输出格式
测试说明
大部分模块基本都可以用随机生成数据的方法,利用代码检测是否符合约束条件。这里说一下需要自己构造样例来验证正确性的模块:判定两个问题是否重复:check_problem.py
check_problem模块思路
当时设计这个模块时,是这样想的:运算符数量小于3的问题,通过有限次交换+和×左右,重复的概率有点大。但是运算符等于3的时候,如果不是一模一样的问题,基本上通过交换重复的概率很小。所以,这个模块的检查思路是:
- 首先直接判断这个问题没交换前,之前是否出现过。出现则返回,未出现则下一步
- 如果是这个问题有3个运算符,直接返回
- 如果这个问题有1个运算符,那么交换运算符左右的数,看这个交换后的问题是否出现过。
- 如果这个问题有2个运算符,统一把问题转化成这样的格式(表达式意义要相同):
(num1 + op1 + num2) + op2 num3。如果op1是加号或者乘号,要保证num1小于等于num2;如果不能转化为上述格式,说明一定不重复,返回即可。转化为这样的格式后,看这个格式的问题之前是否出现过。
测试模块代码
import sys
sys.path.append("../../../")
from module.check_problem import check_problem
if __name__ == "__main__":
test = [
[ [5, "+", 4], [4, "+", 5], ["same"] ],
[ [5, "+", 4], [5, "+", 5], ["diff"] ],
[ [1, "×", 2], [2, "×", 1], ["same"] ],
[ [5, "-", 5], [5, "-", 5], ["same"] ],
[ [5, "÷", 1], [1, "÷", 5], ["diff"] ],
[ [1, "+", 2, "-", 3], [2, "+", 1, "-", 3], ["same"] ],
[ [1, "+", 2, "+", 3], [1, "+", 3, "+", 2], ["diff"] ],
[ [1, "+", 2, "+", 3], [3, "+", "(", 1, "+", 2, ")"], ["same"] ],
[ [1, "+", 2, "+", 3], [3, "+", "(", 2, "+", 1, ")"], ["same"] ],
[ [1, "+", "(", 2, "×", 3, ")"], [2, "×", 3, "+", 1], ["same"] ],
[]
]
flag = True
for problem_list in test :
if len(problem_list) == 0 : break
vis = {}
ok = True
for problem in problem_list :
if len(problem) == 1 : break
ok = check_problem(problem, vis)
if ok == False : break
if ok :
if problem_list.pop() != ["diff"] :
print("Error!!!")
print(problem_list)
flag = False
else :
if problem_list.pop() != ["same"] :
print("Error!!!")
print(problem_list)
flag = False
if flag :
print("Finish test!!!")
样例设计思路
样例:
- \(5 + 4, 4 + 5\ (same)\)
- \(5 + 4, 5 + 5\ (different)\)
- \(1 × 2, 2 × 1\ (same)\)
- \(5 - 5, 5 - 5\ (same)\)
- \(5 ÷ 1, 1 ÷ 5\ (different)\)
- \(1 + 2 - 3, 2 + 1 - 3\ (same)\)
- \(1 + 2 + 3, 1 + 3 + 2\ (different)\)
- \(1 + 2 + 3, 3 + (1 + 2)\ (same)\)
- \(1 + 2 + 3, 3 + (2 + 1)\ (same)\)
- \(1 + (2 × 3), 2 × 3 + 1\ (same)\)
思路:
- 前5个样例是针对一个运算符,后5个样例针对两个运算符
- 1-3个样例,来判断普通的交换是否正确
- 第4个样例,来判断是否能够判定重复问题
- 第5个样例,来判断不能交换的情况
- 第6个样例,来判断普通的交换是否正确
- 第7个样例,来判断优先级问题(运算符优先级相同情况下,从左到右结合)
- 第8个样例,在第7个样例基础上,还要判断整体交换
- 第9个样例,在第8个样例基础上,还要判断括号内部交换
- 第10个样例,验证乘法是否能正确判断
效能分析
making_problem
首先用line_profiler对主程序Myapp.py中的making_problem进行分析,结果如下:
Total time: 10.3257 s
File: Myapp.py
Function: making_problem at line 23
Line # Hits Time Per Hit % Time Line Contents
==============================================================
23 @profile
24 def making_problem(n, r):
25 1 35.0 35.0 0.0 try:
26 1 66.0 66.0 0.0 int(n)
27 1 17.0 17.0 0.0 int(r)
28 except ValueError:
29 print("Error:num处输入的不是整数!")
30 else:
31 1 11014.0 11014.0 0.0 Exer = open('Exercises' + '.txt', "w", encoding='utf-8')
32 1 5698.0 5698.0 0.0 Answ = open('Answers' + '.txt', "w", encoding='utf-8')
33 1 62.0 62.0 0.0 n = int(n)
34 1 18.0 18.0 0.0 r = int(r)
35 1 58228549.0 58228549.0 56.4 problem = gen_problem_list(n, r)
36 1 49.0 49.0 0.0 if n <= 100 :
37 print(problem)
38 1 43752998.0 43752998.0 42.4 answer = cal_problem_list(problem)
39
40 10001 99036.0 9.9 0.1 for i in range(len(problem)):
41 10000 140247.0 14.0 0.1 p = str(problem[i])
42 10000 210919.0 21.1 0.2 p = str(i + 1) + '. ' + p + ' = ' + '\n'
43 10000 235853.0 23.6 0.2 Exer.write(p)
44 1 3185.0 3185.0 0.0 Exer.close()
45
46 10001 89246.0 8.9 0.1 for j in range(len(answer)):
47 10000 124284.0 12.4 0.1 s = str(answer[j])
48 10000 169014.0 16.9 0.2 s = str(j + 1) + '. ' + s + '\n'
49 10000 184081.0 18.4 0.2 Answ.write(s)
50 1 3063.0 3063.0 0.0 Answ.close()
51 1 28.0 28.0 0.0 if n <= 100 :
52 print(answer)
从时间占比可以知道:生成题目集gen_problem_list和计算题目集cal_problem_list这两个模块花费时间最多。
gen_problem_list
接着对gen_problem_list进行分析:
Total time: 6.46569 s
File: test.py
Function: gen_problem_list at line 196
Line # Hits Time Per Hit % Time Line Contents
==============================================================
196 @profile
197 #生成题目集
198 def gen_problem_list(cnt, mod):
199 1 33.0 33.0 0.0 problem_list = []
200 1 17.0 17.0 0.0 vis = {} #记录已经存在的problem
201 1 11.0 11.0 0.0 const_op = ("+", "-", "×", "÷")
202
203 10001 103516.0 10.4 0.2 while cnt:
204 10000 133573.0 13.4 0.2 problem = []
205 while True:
206 11224 27579328.0 2457.2 42.7 problem = gen_problem(int(mod))
207 11224 14091956.0 1255.5 21.8 if check_problem(problem, vis): break
208
209 10000 971476.0 97.1 1.5 vis[str(problem)] = True
210
211 10000 114855.0 11.5 0.2 s = ""
212 75512 817420.0 10.8 1.3 for it in problem:
213 65512 11170373.0 170.5 17.3 if it in (const_op + ("(", ")")): #符号
214 34362 481553.0 14.0 0.7 if it == "(" or it == ")": s += it
215 21150 353209.0 16.7 0.5 else: s += " " + it + " "
216 else: #数字
217 31150 913037.0 29.3 1.4 pre = int(it)
218 31150 5456656.0 175.2 8.4 frac = it - pre
219 31150 1024095.0 32.9 1.6 if frac == 0:
220 15354 289012.0 18.8 0.4 s += str(pre)
221 15796 192367.0 12.2 0.3 elif pre == 0:
222 8925 363270.0 40.7 0.6 s += str(frac)
223 else:
224 6871 321299.0 46.8 0.5 s += str(pre) + "'" + str(frac)
225
226 10000 145811.0 14.6 0.2 problem_list.append(s)
227 10000 134001.0 13.4 0.2 cnt -= 1
228
229 1 9.0 9.0 0.0 return problem_list
刚开始一看似乎并没有什么问题:生成题目gen_problem和检查题目check_problem这两个用的时间最多。但是,细看发现:有一个地方:Line #213,判断竟然用了\(17.3\%\)的时间。
思考片刻后,发现耗时的原因是:每次判断都要从元组中查找这个it,就很耗时间。而我这里只是为了判断it是否为符号。因为代码生成的problem只有数(分数类)和符号,所以考虑用type()函数来解决这个判断问题。修改之后的性能分析:
Total time: 4.79658 s
File: test.py
Function: gen_problem_list at line 200
Line # Hits Time Per Hit % Time Line Contents
==============================================================
200 @profile
201 #生成题目集
202 def gen_problem_list(cnt, mod):
203 1 30.0 30.0 0.0 problem_list = []
204 1 16.0 16.0 0.0 vis = {} #记录已经存在的problem
205 1 12.0 12.0 0.0 const_op = ("+", "-", "×", "÷")
206
207 10001 101018.0 10.1 0.2 while cnt:
208 10000 128066.0 12.8 0.3 problem = []
209 while True:
210 11404 27219434.0 2386.8 56.7 problem = gen_problem(int(mod))
211 11404 7822336.0 685.9 16.3 if check_problem(problem, vis): break
212
213 10000 1030576.0 103.1 2.1 vis[str(problem)] = True
214
215 10000 114895.0 11.5 0.2 s = ""
216 75344 802463.0 10.7 1.7 for it in problem:
217 65344 1002839.0 15.3 2.1 if type(it) != type(const_frac): #符号
218 34244 481529.0 14.1 1.0 if it == "(" or it == ")": s += it
219 21100 345427.0 16.4 0.7 else: s += " " + it + " "
220 else: #数字
221 31100 894772.0 28.8 1.9 pre = int(it)
222 31100 5591981.0 179.8 11.7 frac = it - pre
223 31100 1061854.0 34.1 2.2 if frac == 0:
224 15997 293074.0 18.3 0.6 s += str(pre)
225 15103 177954.0 11.8 0.4 elif pre == 0:
226 9111 352033.0 38.6 0.7 s += str(frac)
227 else:
228 5992 274380.0 45.8 0.6 s += str(pre) + "'" + str(frac)
229
230 10000 143769.0 14.4 0.3 problem_list.append(s)
231 10000 127341.0 12.7 0.3 cnt -= 1
232
233 1 8.0 8.0 0.0 return problem_list
改进后,占比下降到\(2.1\%\),优化幅度还是比较大的。接着看其他模块的分析结果:
gen_num
gen_problem的部分性能分析结果:
Total time: 3.25032 s
File: test.py
Function: gen_problem at line 25
Line # Hits Time Per Hit % Time Line Contents
==============================================================
43 11436 4655755.0 407.1 14.3 num = gen_num(mod)
44 11436 160130.0 14.0 0.5 problem = [num]
45 11436 126071.0 11.0 0.4 last_op = " "
46 33943 393360.0 11.6 1.2 for op in op_list:
47 22731 9196435.0 404.6 28.3 part_num = gen_num(mod)
由此看出生成随机数gen_num是最耗时的,进一步分析gen_num模块:
Total time: 1.43173 s
File: test.py
Function: gen_num at line 4
Line # Hits Time Per Hit % Time Line Contents
==============================================================
4 @profile
5 #生成自然数/真分数
6 def gen_num(mod):
7 36820 567019.0 15.4 4.0 if mod <= 0: return Fraction(0, 1)
8 35403 3022939.0 85.4 21.1 bit = random.randint(1, 10)
9
10 #自然数
11 35403 390743.0 11.0 2.7 if bit >= 1 and bit <= 5:
12 17701 3382916.0 191.1 23.6 return Fraction(random.randint(0, mod - 1), 1)
13 #小于1的真分数
14 17702 190909.0 10.8 1.3 elif (bit >= 6 and bit <= 8) or mod == 1:
15 10661 856153.0 80.3 6.0 down = random.randint(2, mod + 5)
16 10661 878668.0 82.4 6.1 up = random.randint(1, down - 1)
17 10661 1248350.0 117.1 8.7 return Fraction(up, down)
18 #带分数
19 else:
20 7041 598086.0 84.9 4.2 pre = random.randint(1, mod - 1)
21 7041 564771.0 80.2 3.9 down = random.randint(2, mod + 5)
22 7041 581226.0 82.5 4.1 up = random.randint(1, down - 1)
23 7041 2035473.0 289.1 14.2 return pre + Fraction(up, down)
除了随机生成整数比较耗时外,还有一个地方:Line #23的分数加法运算耗时。这时可以做一点小优化:
原来的代码(只有真分数):
pre = random.randint(1, mod - 1)
down = random.randint(2, mod + 5)
up = random.randint(1, down - 1)
return pre + Fraction(up, down)
修改后的代码(自然数与真分数混合,真分数比例大):
down = random.randint(2, max(5, mod))
up = random.randint(down, mod * down - 1)
return Fraction(up, down)
修改后gen_num的分析结果:
Total time: 1.31546 s
File: test.py
Function: gen_num at line 4
Line # Hits Time Per Hit % Time Line Contents
==============================================================
4 @profile
5 #生成自然数/真分数
6 def gen_num(mod):
7 37482 523960.0 14.0 4.0 if mod <= 0: return Fraction(0, 1)
8 36610 3191023.0 87.2 24.3 bit = random.randint(1, 10)
9
10 #自然数
11 36610 401964.0 11.0 3.1 if bit >= 1 and bit <= 5:
12 18263 3587839.0 196.5 27.3 return Fraction(random.randint(0, mod - 1), 1)
13 #小于1的真分数
14 18347 197574.0 10.8 1.5 elif (bit >= 6 and bit <= 8) or mod == 1:
15 11106 903102.0 81.3 6.9 down = random.randint(2, mod + 5)
16 11106 926105.0 83.4 7.0 up = random.randint(1, down - 1)
17 11106 1354695.0 122.0 10.3 return Fraction(up, down)
18 #自然数/真分数(真分数比例大)
19 else:
20 7241 586069.0 80.9 4.5 down = random.randint(2, mod + 5)
21 7241 604605.0 83.5 4.6 up = random.randint(down, mod * down - 1)
22 7241 877707.0 121.2 6.7 return Fraction(up, down)
整体对比
(生成1万道题目,范围为10)
优化前:
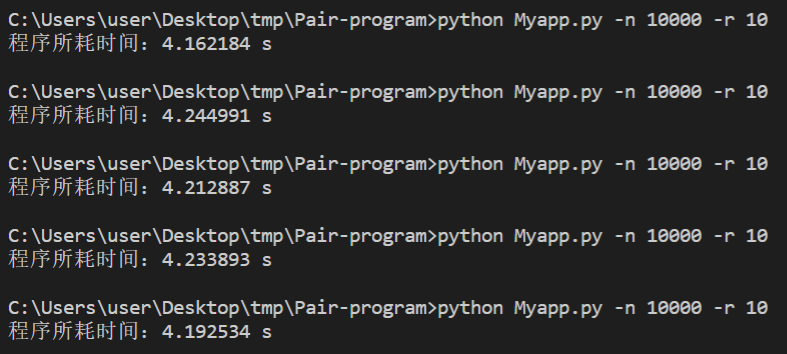
平均4.1s
优化后:
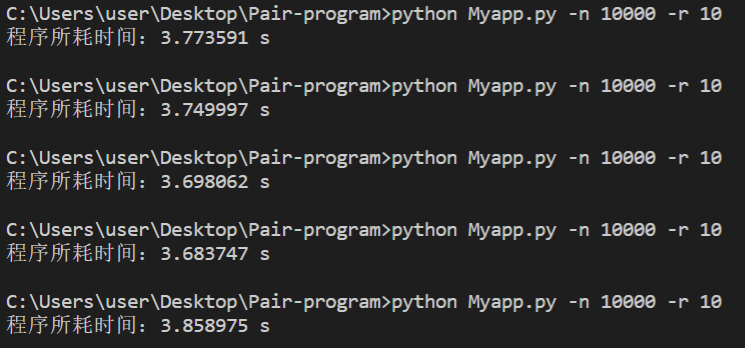
平均3.7s
最终效果
Exercises.txt(题目数量:10,范围:10)
1. 2/7 ÷ (6 × 7) =
2. 4 × (4'9/10 + 8'3/7) × 2 =
3. 7'3/10 ÷ 2 =
4. 9 ÷ (4 ÷ 2'5/7) =
5. 8 + 9 =
6. 4'4/7 + 1/2 =
7. 1 ÷ 1/3 =
8. 1/2 + 8'1/2 =
9. 3/5 + (6'5/9 ÷ (2/3 - 3/7)) =
10. 6 × 7 ÷ 1/4 =
Answers.txt
1. 1/147
2. 106'22/35
3. 3'13/20
4. 6'3/28
5. 17
6. 5'1/14
7. 3
8. 9
9. 28'2/15
10. 168
Grade.txt(题目是上面的Exercises.txt,答案是上面的Answers.txt)
Correct: 10 (1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
Wrong: 0 ()
项目小结
王欢个人感想
-
在实现功能函数时很难做到一次正确,在查找bug时需要写实例进行检验工作。但在后续针对每个模块写单元测试时,发现重复了前面的检验工作,所以可以在函数写好后直接写单元测试进行检验工作。
-
关于结对编程,首先是自己之前的项目没有很好的规划内容,这次两人合作严格按照流程进行合作,将需要做的每一部分内容分析得足够清楚,对后续的实现过程有很大的帮助。
-
结对编程需要很好沟通,结对的同伴在前期准备时教会了我建立共享仓库和配置好编程环境。而且还先一步做好了模块设计,我能够很清楚的知道自己需要做哪些工作。从这次合作中我学习到了如何的规范编程以及规范流程是什么样的等等。
孔止个人感想
这次结对编程,我发现最重要的就是弄好设计文档。为什么这么说?
这次国庆假期,我回了家,但是我的搭档没有回,因此,我们担心可能会有沟通上的问题。在回家后,我立马和搭档一起沟通,看看能不能先弄好文档。接着,经过了多次讨论后,我们弄出了需求分析文档和模块设计文档。
文档的出现,使我们写代码更方便。首先,因为文档已经清楚地说明每个模块需要干什么,而且对应的接口,还有内容格式也都规定好了,就有利于我们独立完成自己负责的模块。在结对项目中,我负责生成题目的模块。其次,文档的出现,还可以使我们的代码更加规范清晰,而不像以前,边想边打代码,打完后又反复改格式。最后,当我们需求发生变换时,只要文档设计地好,模块之间耦合度低,代码更改就变得容易很多。
关于需求分析,刚开始分析需求时,发现:真分数的分母也要小于给定的范围,而且还要求范围可以为1。这时,生成的题目必定全是0之间的运算,就感觉意义不大。根据分析后发现,输入范围小于1,用户应该是想生成一个小于1的真分数。或者说,当范围很小的时候,允许真分数分母大于这个范围,否则就生成不了1万道不重复的题目。所以,我就按照这个规则设计了生成随机数的模块。
关于效率问题,因为之前一直是写C++代码的,所以对C++的运行时间很了解:1s一般能计算1e8次运算。但是,由于这次用的是python,对于生成1万道题目,也就是1e4道题目,竟然需要4s左右。如果加上我生成题目的字符串操作,运算量最多是1e6次。这对于C++来说,1s内绰绰有余;但对于python,似乎要跑的比较久。而且,经过性能分析后,发现python生成随机数也比较久。
总的来说,这次结对编程让我更清晰的认识到软件工程需要干什么事了:需求要分析好,设计文档要写好,写出来的程序效率尽可能高。

