2019 GDUT Rating Contest III : Problem D. Lemonade Line

题面：

D. Lemonade Line

Input file: standard input

Output file: standard output

Time limit: 1 second

Memory limit: 256 megabytes

 

It’s a hot summer day out on the farm, and Farmer John is serving lemonade to his N cows! All N cows (conveniently numbered 1...N) like lemonade, but some of them like it more than others. In particular, cow i is willing to wait in a line behind at most wi cows to get her lemonade. Right now all N cows are in the fields, but as soon as Farmer John rings his cowbell, the cows will immediately descend upon FJ’s lemonade stand. They will all arrive before he starts serving lemonade, but no two cows will arrive at the same time. Furthermore, when cow i arrives, she will join the line if and only if there are at most wi cows already in line.

Farmer John wants to prepare some amount of lemonade in advance, but he does not want to be wasteful. The number of cows who join the line might depend on the order in which they arrive. Help him find the minimum possible number of cows who join the line.

 

Input

The first line contains N, and the second line contains the N space-separated integers w1,w2,...,wN. It is guaranteed that 1 ≤ N ≤ 10^5, and that 0 ≤ wi ≤ 10^9 for each cow i.

 

Output

Print the minimum possible number of cows who might join the line, among all possible orders in which the cows might arrive. 

 

Example

Input

5

7 1 400 2 2 

Output

3

 

Note

In this setting, only three cows might end up in line (and this is the smallest possible).

Suppose the cows with w = 7 and w = 400 arrive first and wait in line.

Then the cow with w = 1 arrives and turns away, since 2 cows are already in line. The cows with w = 2 then arrive, one staying and one turning away.

 

题目描述：

农夫给N头奶牛提供柠檬汁。奶牛们都很喜欢柠檬汁，但是每头奶牛对柠檬汁的“热爱”程度不一样，导致了它们能“忍耐”排队的程度不一样：对于奶牛i来说，最多能“忍耐”W_i头奶牛在前面，如果超过W_i头奶牛，那么奶牛i就不排队取柠檬汁喝了。农夫不想浪费柠檬汁，问：最少需要为多少头牛准备柠檬汁？

 

题目分析：

这道题要注意的是：两头奶牛不会同时到达柠檬汁摊，而且每头奶牛来的时间没有固定（要不然题目怎么 要求 找最小值(￣▽￣)"）。

 

按照题目的意思，其实我们要做的事就是：让尽可能少的奶牛加入队里面。这里用简单的贪心就可以解决：

令“忍耐”度低的奶牛排在后面，离开的可能性更高。或者是：令“忍耐”度高的奶牛排在前面：

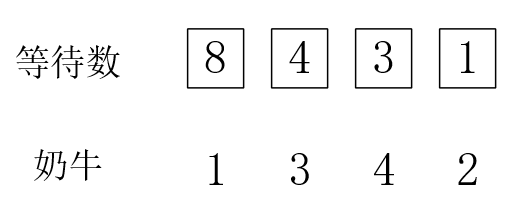
然后，我们可以模拟一下这个过程：

当奶牛1先到达时，因为前面没有奶牛，所以奶牛1加入队列：

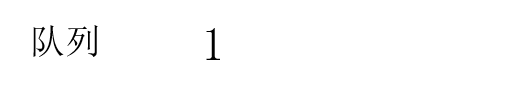
当奶牛3到达时，前面只有1头奶牛，没有超过4，所以奶牛3加入队列：

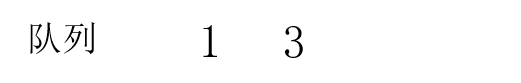
当奶牛4到达时，前面有2头奶牛，没有超过3，所以奶牛4加入队列：

当奶牛2到达时，前面有3头奶牛，超过“忍耐”奶牛数1，所以奶牛2离开：

所以，最终只有3头奶牛留下来，最小值为3。

我们写代码时模拟这个过程就可以了。

 

 

AC代码：

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int maxn = 1e5+5;
int w[maxn];
int cnt;

bool cmp(int a, int b){
    return a > b;
}

int main(){
    int n;
    scanf("%d", &n);
    for(int i = 0; i < n; i++){
        scanf("%d", &w[i]);
    }

    sort(w, w+n, cmp);  //排序

    cnt = 0;
    for(int i = 0; i < n; i++){
        if(cnt <= w[i]){  //能排就排队
            cnt++;
        }
    }

    cout << top << endl;
    return 0;
}