图论相关
内容
并查集
大佬博客：讲的很生动。
邻接表
刚开始学邻接表时，看的是网上的数组模拟链表版本，很久才看懂是什么意思。后面发现白书也有领接表，发现更为简单（早知道看白书了😭）。所以这里我就讲邻接表的简单实现。
vector:
这里的vector是c++ stl的一个容器，可以参见这里。
二维数组存图：
对于这个图来说：
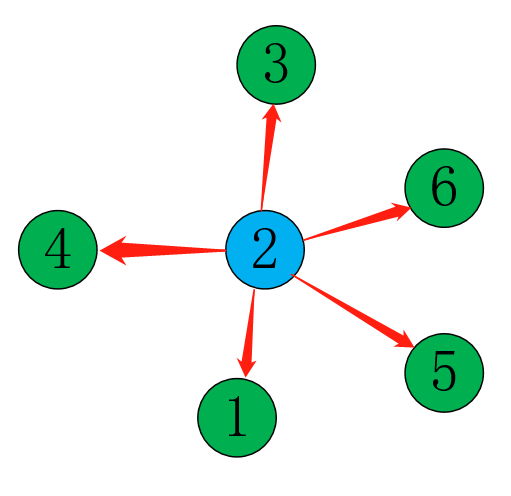
在离散数学中，我们知道可以用一个二维矩阵来存这个图：
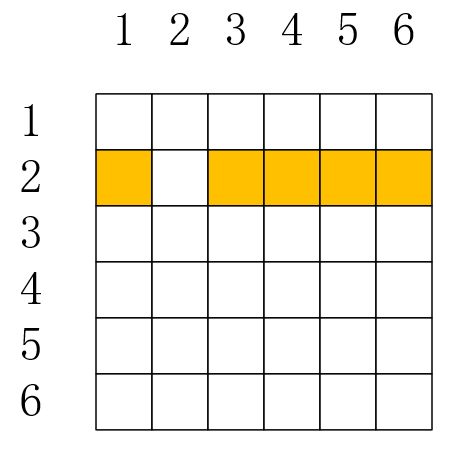
相应地在C语言中要开一个大小为G[7][7]的二维数组，其中：
1.数组全部初始化为0
2.G[u][v] == 1代表u和v之间有一条边，G[u][v] == 0代表u和v之间没有直接相连的边
于是我们可以这样存图：当数组全都初始化为0后，G[2][1] = 1, G[2][3] = 1, G[2][4] = 1, G[2][5] = 1, G[2][6] = 1。
但是，我们发现：这个二维数组有一片很大的空间，没有存储其他边的信息。假如有10的5次方这么多个点，在C/C++中是开不了这么大的数组（10的10次方，超过一亿了）。那我们如何高效地存下这些边，摒弃无用的信息？答案就是邻接表。
邻接表：
还是这个图：
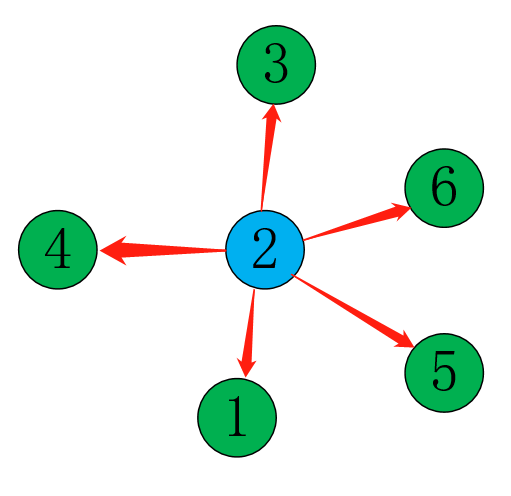
我们通过观察发现：源点是2，而它的邻接点是：1，3，4，5，6。所以，我们可不可以用一个方法，存：以源点为核心，然后通过这个源点来遍历所有的邻接点的图？答案就是这样存（vector数组实现）：
1 #include <cstdio> 2 #include <iostream> 3 #include <vector> 4 using namespace std; 5 vector<int> G[7]; 6 int u = 2; 7 int to[7] = {1,3,4,5,6}; 8 9 int main(){ 10 for(int i = 0; i < 5; i++){ 11 G[u].push_back(to[i]); 12 } 13 return 0; 14 }
遍历边的方式（知道源点u）：
1 int u = 2; 2 for(int i = 0; i < G[u].size(); i++){ 3 printf("%d ", G[u][i]); 4 }
为什么这样可以节省空间？因为我们用了vector的特点：不定长。当要加入元素时，vector就会自动申请空间。可能有的同学就有疑问：可不可以用链表实现？当然可以，只不过因为acm的缘故，这个邻接表的实现方法是最简便的，想要追求速度，可以用链表代替vector。另外还有一种常见的实现方式：数组模拟链表，这里我就不多讲了，网上很多实现方式，重点还是要理解邻接表的核心（以点为中心，存边）是什么，抓住重点看应该会好很多。下面给出做题模板：
1 #include <cstdio> 2 #include <iostream> 3 #include <vector> 4 using namespace std; 5 const int maxn = 1e5+5; 6 int n, m; //n:点的数量 m:边的数量 7 struct edge{ //一般关于图的问题中, 边都是由权值的，这里就用结构体存边 8 int to, cost; 9 //to:邻接点 cost:邻接边的权值 10 }; 11 vector<edge> G[maxn]; //vector数组存边 12 13 int main(){ 14 scanf("%d%d", &n, &m); 15 int u, v, cost; //u:源点 v:目标点 cost:权值 16 edge temp; //临时的边 17 18 for(int i = 0; i < m; i++){ 19 scanf("%d%d%d", &u, &v, &cost); 20 temp.cost = cost; 21 22 temp.to = v; 23 G[u].push_back(temp); 24 //如果是双向的边, 还要加语句: temp.to = u; G[v].push_back(temp); 25 } 26 return 0; 27 }
Dijkstra算法
当初自己看的一篇比较友好的博客：点我
解决什么问题：从一个点（称为源点）到剩余所有点的距离。
基本思想：贪心
算法过程：每次从：离源点最近，且未访问过的点，去更新邻接点到源点的距离。
过程讲述：
图：
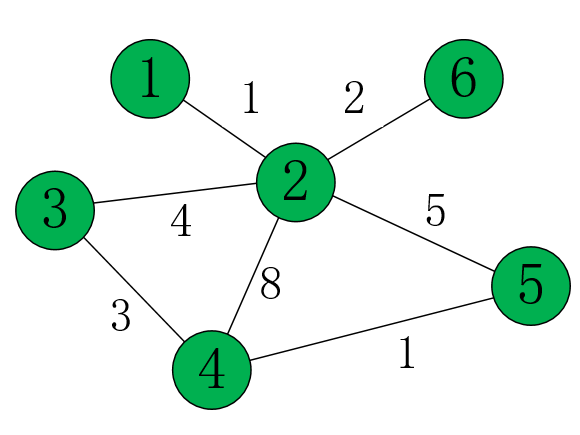
我们要计算：从1到各个点的最短距离。
刚开始应该是这样：
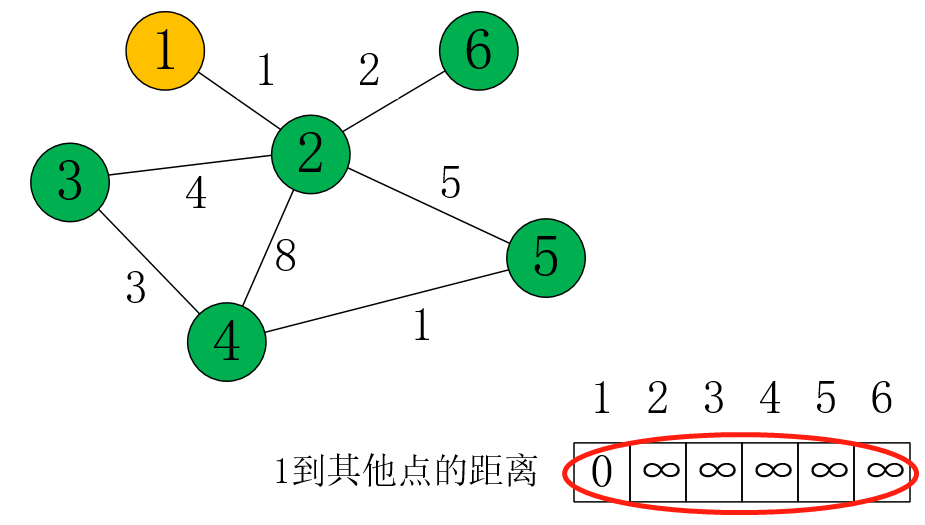
自己到自己的距离初始化为0，其余设为无穷大。
从源点1开始，它的邻接点是2，所以1到2的距离更新为dis[1]+1 = 1。
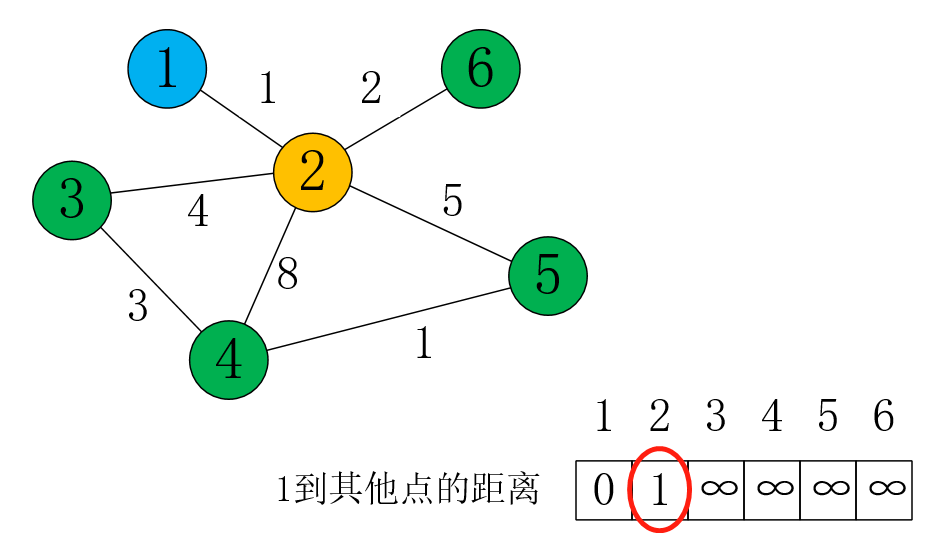
这时，离源点1的最近，且没作为“主动更新”的点是2，所以我们从2开始，去更新它的邻接点：
dis[3] = dis[2] + 4 = 5
dis[4] = dis[2] + 8 = 9
dis[5] = dis[2] + 5 = 6
dis[6] = dis[2] + 2 = 3
更新完后：
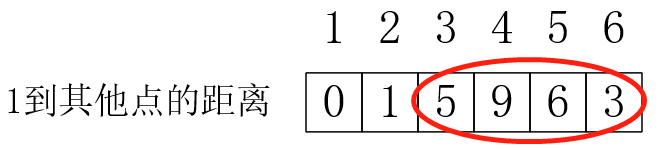
我们发现，这时离源点最近，且没作为“主动更新“的点是6，所以从6开始更新邻接点：
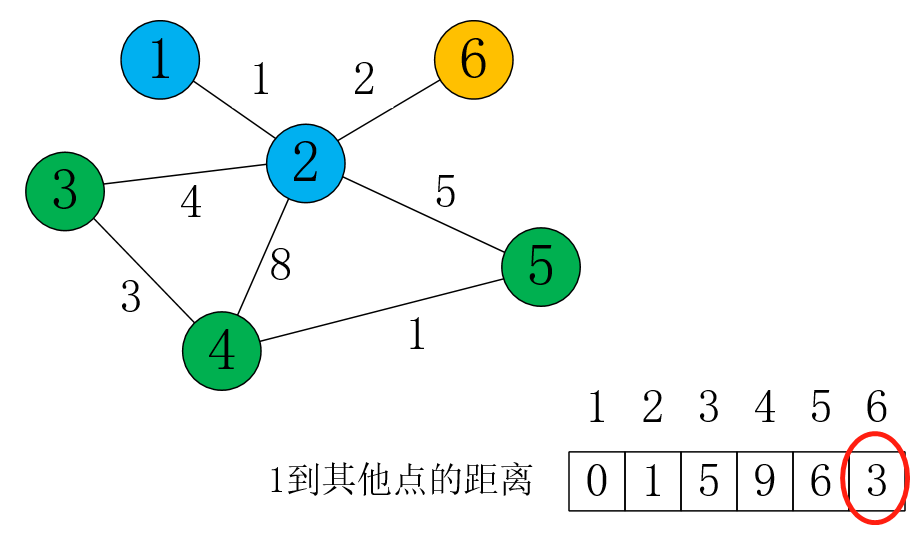
在更新点2时，因为dis[6] + 2 = 3 + 2 = 5 > dis[2] = 1，所以不更新dis[2]。
接下来，离源点最近，且没作为“主动更新”的点是3，所以从3开始更新邻接点：
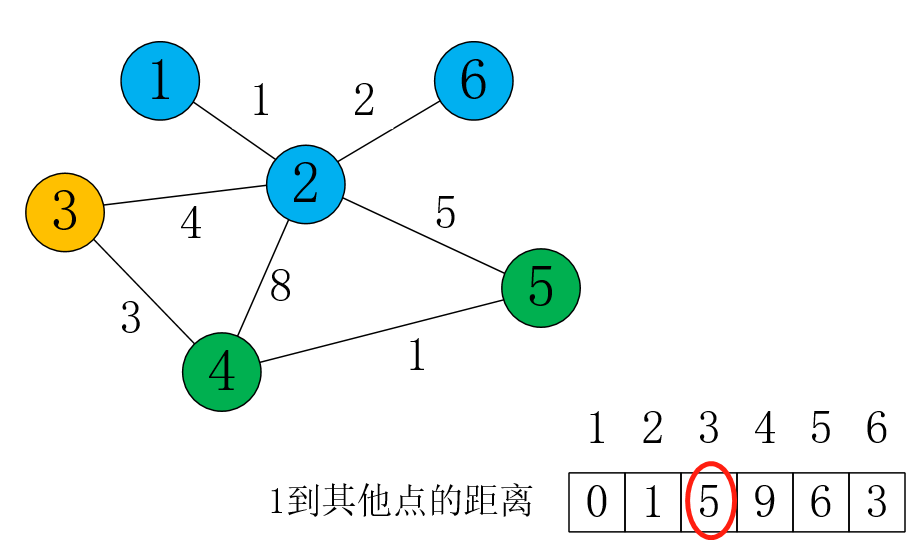
这时：dis[3] + 3 = 6 < dis[4] = 9，所以更新dis[4]为6；dis[3] + 2 = 7 > dis[2] = 1，所以不更新dis[2]。
更新完后就是这样：
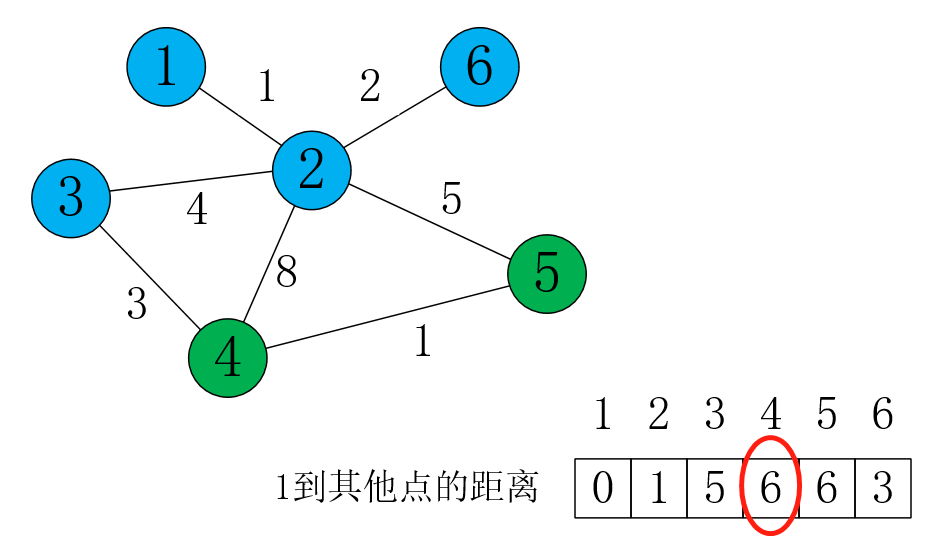
这时，离源点最近，且没作为“主动更新”的点有4和5，所以随便选一个点来更新。最终的更新结果：
写成代码（领接表实现）：
1 #include <cstdio> 2 #include <iostream> 3 #include <vector> 4 using namespace std; 5 const int maxn = 1e5+5; 6 const int inf = 1e9; 7 int n, m; 8 struct edge{ 9 int to, cost; 10 }; 11 vector<edge> G[maxn]; 12 13 int dis[maxn]; //到源点的距离 14 int vis[maxn]; //“主动更新”点的标记 15 16 void dijkstra(){ 17 //初始化 18 for(int i = 1; i <= n; i++){ 19 dis[i] = inf; 20 } 21 dis[1] = 0; 22 23 while(1){ 24 //找离源点最近, 且未“主动更新”别人的点 25 int minn = 1e9, u = -1; 26 for(int i = 1; i <= n; i++){ 27 if(vis[i] == 0 && dis[i] > minn){ 28 minn = dis[i]; 29 u = i; 30 } 31 } 32 if(u == -1) break; //找不到说明所有点已更新完毕, 退出即可 33 34 vis[u] = 1; //打上标记 35 36 int to, cost; 37 //更新邻接点 38 for(int i = 0; i < G[u].size(); i++){ 39 to = G[u][i].to; 40 cost = G[u][i].cost; 41 if(dis[to] > dis[u]+cost){ 42 dis[to] = dis[u]+cost; 43 } 44 } 45 } 46 } 47 48 int main(){ 49 //输入同邻接表 50 scanf("%d%d", &n, &m); 51 int u, v, cost; 52 edge temp; 53 54 for(int i = 0; i < m; i++){ 55 scanf("%d%d%d", &u, &v, &cost); 56 temp.cost = cost; 57 58 temp.to = v; 59 G[u].push_back(temp); 60 temp.to = u; 61 G[v].push_back(temp); 62 } 63 64 dijkstra(); //dijkstra算法 65 66 return 0; 67 }
代码比较长，要有耐心看（〃｀ 3′〃）（可能会有些小错误，欢迎指正ヾ(•ω•`)o）
这个算法的时间复杂度是O(n*m)，当点n == 1e5(10的5次方)，m == 1e5时，这个复杂度要爆炸！是O(1e10)的复杂度。我们设计出来的算法时间复杂度应该要小于O(1e7)（极限1e8），才能在1s内运行完，否则会超时。那么我们怎么优化时间呢？
我们发现，每个边肯定是要遍历的，所以这里的m优化不了，那只能优化n了，n的复杂度在代码中是：找离源点最近的点。如果我们能节省这部分的时间，就可以优化成功。这里较好的解决办法是用优先队列（C++ STL，内部用数据结构：“堆”，来实现），可以把n优化成logn，然后复杂度变成了O(logn * m)。当n == 1e5时，logn大概是17，也就是总的复杂度是O(1e6)，完全可以接受。我这里直接给出代码：
1 #include <cstdio> 2 #include <iostream> 3 #include <vector> 4 #include <queue> 5 using namespace std; 6 const int maxn = 1e5+5; 7 const int inf = 1e9; 8 int n, m; 9 struct edge{ 10 int to, cost; 11 }; 12 vector<edge> G[maxn]; 13 14 int dis[maxn]; //到源点的距离 15 int vis[maxn]; //“主动更新”点的标记 16 17 struct cmp{ 18 bool operator () (int a, int b){ 19 return dis[a] > dis[b]; //注意这里的比较级 20 } 21 }; 22 23 void dijkstra(){ 24 //初始化 25 for(int i = 1; i <= n; i++){ 26 dis[i] = inf; 27 } 28 dis[1] = 0; 29 30 priority_queue<int, vector<int>, cmp> q; //创建队列 31 32 int u; 33 while(!q.empty()){ 34 u = q.top(); q.pop(); //取出离源点最近的点, 然后弹出队列 35 if(vis[u]) continue; //被作为“主动更新”的点就跳过 36 37 vis[u] = 1; //打上标记 38 39 int to, cost; 40 //更新邻接点 41 for(int i = 0; i < G[u].size(); i++){ 42 to = G[u][i].to; 43 cost = G[u][i].cost; 44 if(dis[to] > dis[u]+cost){ 45 dis[to] = dis[u]+cost; 46 q.push(to); 47 } 48 } 49 } 50 } 51 52 int main(){ 53 //输入同邻接表 54 scanf("%d%d", &n, &m); 55 int u, v, cost; 56 edge temp; 57 58 for(int i = 0; i < m; i++){ 59 scanf("%d%d%d", &u, &v, &cost); 60 temp.cost = cost; 61 62 temp.to = v; 63 G[u].push_back(temp); 64 temp.to = u; 65 G[v].push_back(temp); 66 } 67 68 dijkstra(); //dijkstra算法 69 70 return 0; 71 }
Bellman-Ford算法
Floyd-Warshall算法
网上有很多解释，这里仅给出模板和用法：
用在什么地方：需要求任意两点间的最短路。复杂度：O(n^3)
模板：
1 #include <cstdio> 2 #include <iostream> 3 using namespace std; 4 const int maxn = 1005; 5 const int inf = 1e9; //无穷大 6 int n, m; //n:点的数量 m:边的数量 7 int G[maxn][maxn]; //图 8 9 int main(){ 10 scanf("%d%d", &n, &m); 11 int u, v, cost; //u:源点 v:终点 cost:权值 12 13 //初始化 14 for(int i = 1; i <= n; i++){ 15 for(int j = 1; j <= n; j++){ 16 G[i][j] = inf; 17 } 18 G[i][i] = 0; 19 } 20 21 //输入边 22 for(int i = 0; i < m; i++){ 23 scanf("%d%d%d", &u, &v, &cost); 24 G[u][v] = cost; 25 } 26 27 //Floyd算法 28 for(int i = 1; i <= n; i++){ 29 for(int j = 1; j <= n; j++){ 30 for(int k = 1; k <= n; k++){ 31 if(G[i][j] > G[i][k] + G[k][j]) 32 G[i][j] = G[i][k] + G[k][j]; 33 //可以这样记:如果有中转站k,使得i-k的距离+k-j的距离小于i-j的直接距离,那么更新 34 } 35 } 36 } 37 38 return 0; 39 }
Prime算法
Kruskal算法
暂更
