HDU 1114 Piggy-Bank
题面:
Piggy-Bank
Input file: standard input
Output file: standard output
Time limit: 1 second
Memory limit: 256 megabytes
Before ACM can do anything, a budget must be prepared and the necessary financial support obtained. The main income for this action comes from Irreversibly Bound Money (IBM). The idea behind is simple. Whenever some ACM member has any small money, he takes all the coins and throws them into a piggy-bank. You know that this process is irreversible, the coins cannot be removed without breaking the pig. After a sufficiently long time, there should be enough cash in the piggy-bank to pay everything that needs to be paid.
But there is a big problem with piggy-banks. It is not possible to determine how much money is inside. So we might break the pig into pieces only to find out that there is not enough money. Clearly, we want to avoid this unpleasant situation. The only possibility is to weigh the piggy-bank and try to guess how many coins are inside. Assume that we are able to determine the weight of the pig exactly and that we know the weights of all coins of a given currency. Then there is some minimum amount of money in the piggy-bank that we can guarantee. Your task is to find out this worst case and determine the minimum amount of cash inside the piggy-bank. We need your help. No more prematurely broken pigs!
Input
The input consists of T test cases. The number of them (T) is given on the first line of the input file. Each test case begins with a line containing two integers E and F. They indicate the weight of an empty pig and of the pig filled with coins. Both weights are given in grams. No pig will weigh more than 10 kg, that means 1 <= E <= F <= 10000. On the second line of each test case, there is an integer number N (1 <= N <= 500) that gives the number of various coins used in the given currency. Following this are exactly N lines, each specifying one coin type. These lines contain two integers each, Pand W (1 <= P <= 50000, 1 <= W <=10000). P is the value of the coin in monetary units, W is it's weight in grams.
Output
Print exactly one line of output for each test case. The line must contain the sentence "The minimum amount of money in the piggy-bank is X." where X is the minimum amount of money that can be achieved using coins with the given total weight. If the weight cannot be reached exactly, print a line "This is impossible.".
Example
Input
3
10 110
2
1 1
30 50
10 110
2
1 1
50 30
1 6
2
10 3
20 4
Output
The minimum amount of money in the piggy-bank is 60.
The minimum amount of money in the piggy-bank is 100.
This is impossible.
题目描述:
ACM协会里面有个储钱罐,ACM成员会把硬币放进储钱罐。现在知道储钱罐为空时的重量和储钱罐装了硬币之后的重量,还知道储钱罐里面一些硬币的种类(包含面额和重量), 如果能推算储钱罐存的钱的最小值,就按题目要求输出这个最小值,否则,输出不可能推算出。
题目分析:
这题是经典背包问题之完全背包问题,只是有一点点不同。这题也可以用普通dp的思路去解决,我讲一下我的思路(大佬勿喷)是怎样的:
首先,我们要重新定义这个问题,我是这样定义的:用这些硬币(硬币的种类给出来了)能凑够重量为V时,硬币总额的最小值。显然,子问题就是用这些硬币能凑够重量为 j 时(0 <= j < V),硬币总额的最小值。我们看看这两个问题有什么联系:假如,我已经求出了全部子问题的结果,并且保存在一个dp数组里面,dp[ j ]就是用给出种类的硬币,能够凑成重量为 j 时(0 <= j <= V),硬币总额的最小值,那么,如何利用这些值来求出我们的刚开始定义的问题:用这些硬币能够凑成重量为V时,硬币总额的最小值?也就是求dp[V]。当 j + W[ i ] == V时 (W[ i ] 是某种硬币的重量,i 是种类),dp[V] = dp[ j ] + P[ i ] (P[ i ] 是某种硬币的面额,i 是种类)。如果我们从1-N遍历一次 i 的种类,然后取其中的最小值,这样得出来的dp[V]就是最优的。那么dp[ j ]怎么求?其实和dp[V]的求法是一样的。我们举个例子:
储钱罐里面的总硬币重量:9硬币种类: 面额 重量1 2 42 3 33 1 4
当我们选第一种硬币时,状态是:
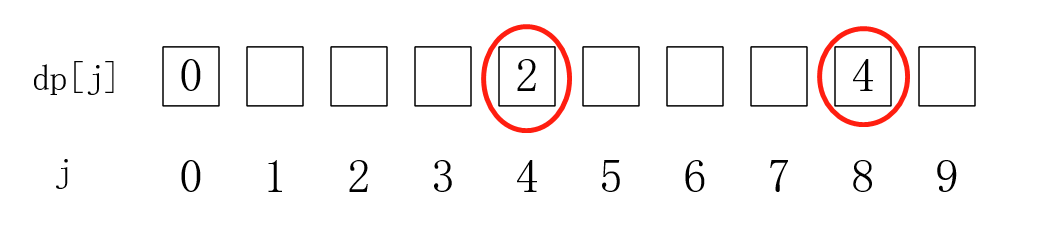
这是选择第一种硬币时,所有dp[ j ]的最佳值,当我们选择第二种硬币时:
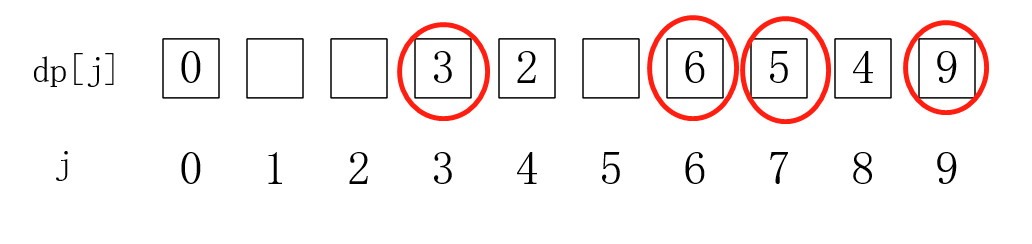
(注:圈圈是被更新的值)
我们来慢慢分析是怎样进行更新的:
首先,我们从 j == 0出发,当选择一个硬币时,重量和面额就会增加,也就是dp[3] = dp[0] + 3 = 3。
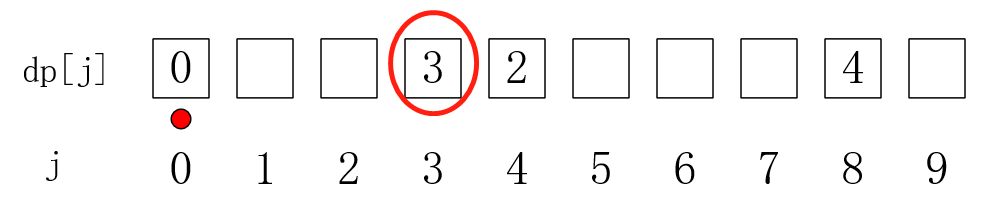
接下来,我们发现 j == 2时,没有被更新,所以不管它,j == 2时也同理。
j == 3时,我们发现之前被更新过了,所以我们在这个基础上,加上第二个种类的硬币(加一个),然后就会更新dp[6],dp[6] = dp[3] + 3:

更新了dp[6]后,我们的 j 继续往前,到 j == 4:
j == 4时,发现dp[4]被更新过,所以从这点出发,加上第二个种类的硬币(加一个),然后就会更新dp[7],dp[7] = dp[4] + 3:
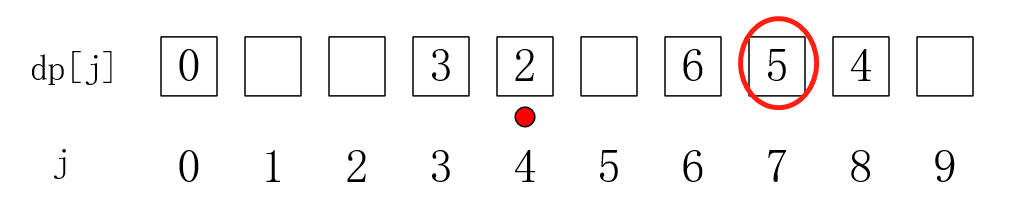
j == 5时,因为dp[5]不存在,所以直接跳过。
j == 6时,发现dp[6]被更新过,所以从这点出发,加上第二个种类的硬币(加一个),然后就会更新dp[9],dp[9] = dp[6] + 3:
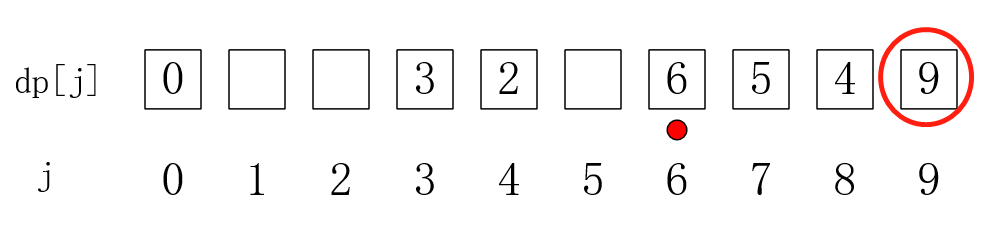
j == 7时,更新不了后面的dp。j == 8和 j == 9同理。
这时,选第二种硬币更新完后,我们会得到选前两种硬币的dp数组,而且这些dp数组存的都是最优(最小的,没被更新到的dp[ j ]就是设为无穷大),有的人可能想问:为什么不这样子更新:
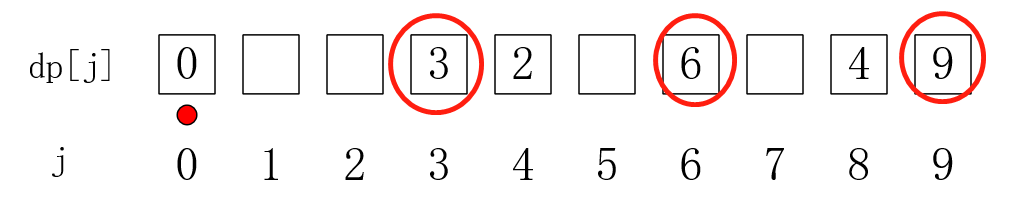
(更新方法:当 j == 0时,从当前基础上,选1个第二种硬币,更新dp[3];选2个第二种硬币,更新dp[9];选3个第二种硬币,更新dp[9],直到更新到末尾)
其实也不是不行,就是会导致重复更新,然后时间复杂度更大了:
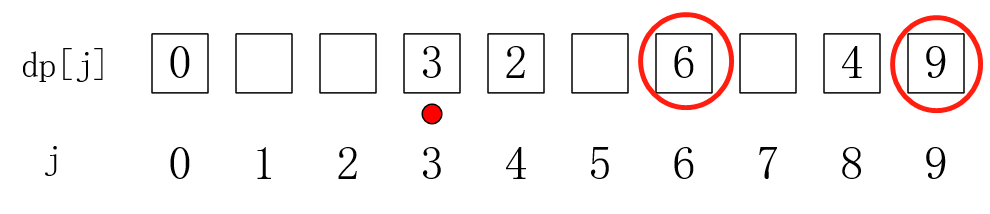
(当 j == 3时,又会去更新后面的值,其实后面早就更新过了)
如果还没理解,可以自己慢慢去体会一下上面的过程(每次只加一个硬币)
当开始选择第三种硬币时:
j == 0时,发现dp[0]存在,所以我们从dp[0]更新后面的dp[4],dp[4] = dp[0] + 1 = 1,发现这时算出来的dp[4]和之前的dp[4] = 2要小,所以我们要小的值(题目说要最小值)。为什么可以直接更新呢,不需要保留dp[4] = 2这个状态吗?dp其实是不管之前具体的状态是什么,只要取之前某个最优的状态,就能达到最优。所以我们直接更新就好了:
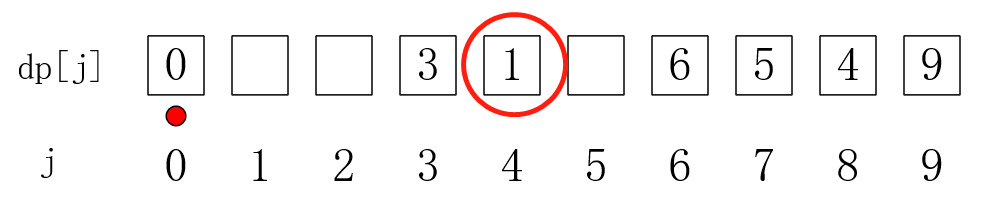
j == 3时,更新dp[7];j == 4时,更新dp[8];j == 5时,更新dp[9]??????
dp[5]都没有被更新过(其实没被更新过的意思就是:不能用之前种类的硬币凑成这个重量,这个之前忘记说了),当然不能更新dp[9]了。
更新后,就变成这样了:
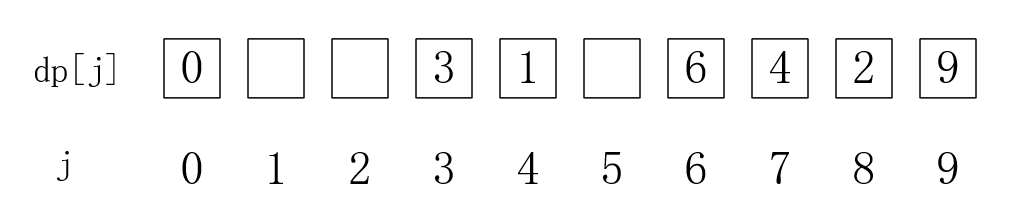
这时,dp[V]就是我们想要的答案了。
关于dp的各种小疑问:
1.dp[ j ]有什么用(除了用来计算dp[V]之外):
当然有用啊。除了V改成6外,其他的都不变,那么上面的dp[6]就是答案了。也就是说,数组里面存放的是每一个状态的最优值,理解这个有助于帮助理解dp
2.这道题的状态转移方程是什么?
dp[ i ][ j ] = min(dp[ i-1 ][ j ], dp[ i ][ j-W[ i ] ] + P[ i ] ) ( j >= W[ i ] )dp[ i ][ j ] = dp[ i-1 ][ j ] ( j < W[ i ] )
其中:dp[ i-1 ][ j ]是指不选第 i 种硬币(也就是直接利用上一次计算的结果)
dp[ i-1 ][ j-W[ i ] ]是指选了第 i 种硬币的结果(加一个硬币)
有的人可能会以为这个是状态转移方程:
dp[ j ] = min(dp[ j ], dp[ j-W[i] ]+P[ i ] )
但其实不是,这里只是一种更新手段,为什么这样说呢?当我们结束了 i-1 次的更新,还没开始更新第 i 次(也就是状态 i )时,这时dp[ j ]数组里面存的值都是dp[ i-1 ][ j ]的值,所以,我们只要直接和 dp[ j-W[ i ] ] + P[ i ]比较大小,看哪个小就比较哪个,所以就会有上面的式子。
3.为什么我不按照状态方程讲?
因为我还没理解dp前,直接去理解dp的更新,也就是直接去思考出问题2的第二个式子,回过头来发现这并不是状态方程,而是代码是直接这样写的。反正能理解问题2的第二个式子就直接去理解,不能的话还是先理解状态方程先吧。(自己水的一批🙃)
AC代码:
直接想:一维数组:
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 using namespace std; 5 const int inf = 0x3f3f3f3f; 6 int P[505], W[505]; 7 int dp[10005]; 8 int n; 9 10 int main(){ 11 int t; 12 cin >> t; 13 while(t--){ 14 //初始化 15 memset(dp, inf, sizeof(dp)); 16 memset(P, 0, sizeof(P)); 17 memset(W, 0, sizeof(W)); 18 19 int E, F; 20 cin >> E >> F; 21 cin >> n; 22 for(int i = 1; i <= n; i++) 23 cin >> P[i] >> W[i]; 24 25 int V = F-E; 26 dp[0] = 0; //初始化 27 for(int i = 1; i <= n; i++){ 28 for(int j = W[i]; j <= V; j++){ 29 dp[j] = min(dp[j], dp[j-W[i]]+P[i]); //更新式子 30 } 31 } 32 33 if(dp[V] == inf) cout << "This is impossible.\n"; 34 else cout << "The minimum amount of money in the piggy-bank is " << dp[V] << ".\n"; 35 } 36 return 0; 37 }
二维数组(状态方程,未优化空间):
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 using namespace std; 5 const int inf = 0x3f3f3f3f; 6 int P[505], W[505]; 7 int dp[505][10005]; 8 int n; 9 10 int main(){ 11 int t; 12 cin >> t; 13 while(t--){ 14 //初始化 15 memset(dp, inf, sizeof(dp)); 16 memset(P, 0, sizeof(P)); 17 memset(W, 0, sizeof(W)); 18 int E, F; 19 cin >> E >> F; 20 cin >> n; 21 for(int i = 1; i <= n; i++) 22 cin >> P[i] >> W[i]; 23 24 int V = F-E; 25 dp[0][0] = 0; 26 27 for(int i = 1; i <= n; i++){ 28 for(int j = 0; j <= V; j++){ 29 if(j < W[i]) dp[i][j] = dp[i-1][j]; 30 else dp[i][j] = min(dp[i-1][j], dp[i][j-W[i]]+P[i]); 31 } 32 } 33 34 if(dp[n][V] == inf) cout << "This is impossible.\n"; 35 else cout << "The minimum amount of money in the piggy-bank is " << dp[n][V] << ".\n"; 36 } 37 return 0; 38 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号