HDU 2602 Bone Collector

题面：

传送门

Bone Collector

Input file: standard input

Output file: standard output

Time limit: 1 second

Memory limit: 256 megabytes

 

Many years ago , in Teddy’s hometown there was a man who was called “Bone Collector”. This man like to collect varies of bones , such as dog’s , cow’s , also he went to the grave …
The bone collector had a big bag with a volume of V ,and along his trip of collecting there are a lot of bones , obviously , different bone has different value and different volume, now given the each bone’s value along his trip , can you calculate out the maximum of the total value the bone collector can get ?

 

Input

The first line contain a integer T , the number of cases.
Followed by T cases , each case three lines , the first line contain two integer N , V, (N <= 1000 , V <= 1000 )representing the number of bones and the volume of his bag. And the second line contain N integers representing the value of each bone. The third line contain N integers representing the volume of each bone.

 

Output

One integer per line representing the maximum of the total value (this number will be less than 2³¹).

 

Example

Input

1

5 10

1 2 3 4 5

5 4 3 2 1

Output

14

 

题目描述：

“骨头收集者”有一个体积为V的背包。在路途上有很多不同体积，不同价值的骨头。计算“骨头收集者”最大能收集到的骨头价值。

 

题目分析：

这题是经典01背包问题。假如我们用朴素的搜索方法（dfs）来解决（每个物品选或不选），那么，复杂度是O(2ⁿ)，在这里肯定会超时。我们可以用记忆化搜索来解决这个问题。首先我们看看如果用朴素方法时要怎么解决：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 1005;
int n, v;
int value[maxn], volume[maxn];

int dfs(int i, int left){
    if(i == n+1)     //没有物品可选了
        return 0;
    else if(left < volume[i])   //选不了第i个物品，也就是不选
        return dfs(i+1, left);
    else
        return max(dfs(i+1, left), dfs(i+1, left-volume[i])+value[i]);
        //选和不选都尝试一下，取最大的
}

int main(){
    int t;
    cin >> t;
    while(t--){
        cin >> n >> v;
        for(int i = 1; i <= n; i++) cin >> value[i];
        for(int i = 1; i <= n; i++) cin >> volume[i];

        cout << dfs(1, v) << endl;
    }
    return 0;
}

我们看dfs的代码：其实就是在第i个物品中进行决策：选与不选。如果不选第i个物品，那么就直接取：除了第i个物品之外，确定完后面所有物品（i+1 -- n）的选择时，背包容量为left决策的结果。这里比较关键：为什么是第i个后面所有的物品，不应该只是第i+1个物品的决策吗？其实，因为在dfs时我们会有回溯（return）的操作，所以当我们取dfs(i+1, left)的值时，就是后面的物品已经决策好的结果。理解了这个，后面的都很好理解；如果选第i个物品，就要把第i个物品装到背包里面去，剩余容量变为left-volume[i]。也就是说，我们要找决策完第i个后面所有物品，背包容量为left-volume[i]的结果。最后，在这两者选择之间取最大的那个选择（题目要求取最大嘛）作为结果返回（如果选不了当然只能取不选i物品的结果返回）。如果对这里的dfs理解不好听到后面就会完全懵了，建议先慢慢理解上面的代码再继续往下看。

 

理解完这个后，我们会发现，中间有些重复计算的地方，举个例子：

输入：T = 1, N = 4, V = 5

value：3 2 4 2

volume：2 1 3 2

（这里借了白书的数据，题目的样例比较难画递归图）

递归调用图：

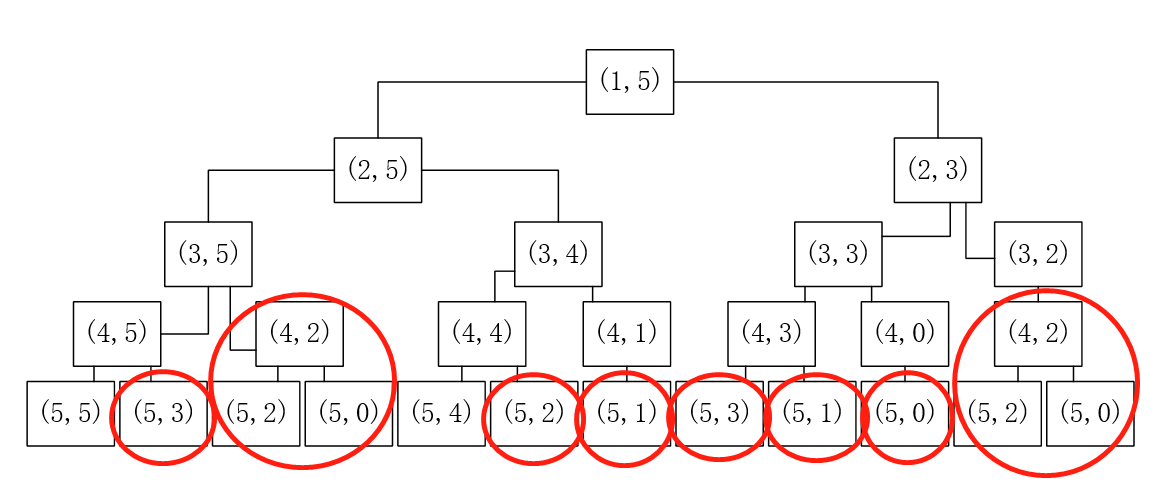
由这张图我们可以看到，在递归调用时，我们做了很多重复的计算，比如要算dfs(4，2)的值时，在dfs(3，5)时算了一遍，在dfs(3，2)时又算了一遍。由于这里的两个dfs(4，2)调用的参数相同，结果自然相同，其他圈圈类似。所以，我们要解决再次算某一个dfs时，避免重复计算。答案自然是之前算过一次的话就记录在数组里面，下次还计算这个值的时候直接用就行了，不需要递归下去，代码：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 1005;
int n, v;
int value[maxn], volume[maxn];
int dp[maxn][maxn];   //记忆化数组

int dfs(int i, int left){
    if(dp[i][left] != 0) return dp[i][left];
    if(i == n+1)     //没有物品可选了
        dp[i][left] = 0;
    else if(left < volume[i])   //选不了第i个物品
        dp[i][left] = dfs(i+1, left);
    else
        dp[i][left] = max(dfs(i+1, left), dfs(i+1, left-volume[i])+value[i]);
        //选和不选都尝试一下，取最大的
    return dp[i][left];  
}

int main(){
    int t;
    cin >> t;
    while(t--){
        memset(dp, 0, sizeof(dp));   //每次都要记得清空数组
        cin >> n >> v;
        for(int i = 1; i <= n; i++) cin >> value[i];
        for(int i = 1; i <= n; i++) cin >> volume[i];

        cout << dfs(1, v) << endl;
    }
    return 0;
}

这时候的时间复杂度我们可以计算一下：由于之前算过的值会记录在dp数组里面，所以最坏的时间复杂度为O(N*V)。相比于之前的O(2ⁿ)，的确优化了不少的时间。这种方法又叫做记忆化搜索，是dp（动态规划）的一种实现方式。不过，dp的核心可不是记忆化搜索，而是我们想出dfs的方法：每个物品进行选和不选的决策，当对第i个物品进行决策时，决策的结果会用到对第i+1个物品进行决策的结果，如此递归下去，最终对第i个物品决策时，用到的是第i个物品之后的物品的决策结果。当决策完第i个物品后，会把第i个物品最优的结果回溯给第i-1个物品，帮助第i-1个物品的决策。如果把选每个物品的状态用一个点表示，示意图就是：

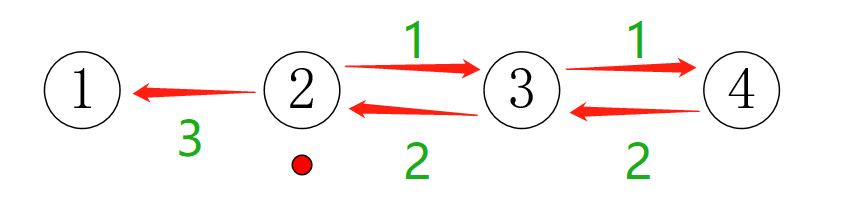
这样，当我们输出dfs(1，v)时，就是最终的答案。而记忆化数组只是帮助我们避免重复计算我们算好的结果。dp问题最重要的是根据状态和子状态（问题和子问题），想出状态转移方程。这里的状态转移方程就是（用记忆化数组表示）：

dp[n+1][left] = 0   (0 <= left <= V)           //相当于初始化

dp[i][left] = dp[i+1][left]     ( j < w[i] )

dp[i][left] = max(dp[i+1][left], dp[i+1][ left-volume[i] ]+value[i] )    ( j >= w[i] )

根据上面的状态转移方程和我们对dfs的分析，其实也可以将上面的代码写成递推（循环）的形式：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 1005;
int n, v;
int value[maxn], volume[maxn];
int dp[maxn][maxn];   //记忆化数组

int main(){
    int t;
    cin >> t;
    while(t--){
        memset(dp, 0, sizeof(dp));   //每次都要记得清空数组
        cin >> n >> v;
        for(int i = 1; i <= n; i++) cin >> value[i];
        for(int i = 1; i <= n; i++) cin >> volume[i];

        for(int i = n; i >= 1; i--){  //从后面往前面更新
            for(int left = 0; left <= v; left++){   //left从0-V或者从V-0都是一样的
                if(left < volume[i]) dp[i][left] = dp[i+1][left];
                else{
                    dp[i][left] = max(dp[i+1][left], dp[i+1][left-volume[i]]+value[i]);
                }
            }
        }

        cout << dp[1][v] << endl;
    }
    return 0;
}

理解了之前的东西，我们可以再继续改进一下：之前我们是通过第i个物品后的决策推出第i个物品的决策，也就是从后往前推。现在我们也可以从前往后推，也就是从前面去更新后面，只需要改一下这个递推和输出结果就行了：

for(int i = 1; i <= n; i++){  //从前面往后面更新
    for(int left = 0; left <= v; left++){   //left从0-V或者从V-0都是一样的
        if(left < volume[i]) dp[i][left] = dp[i-1][left];
        else{
            dp[i][left] = max(dp[i-1][left], dp[i-1][left-volume[i]]+value[i]);
        }
    }
}

cout << dp[n][v] << endl;

状态转移方程：

dp[0][left] = 0   (0 <= left <= V)           //相当于初始化

dp[i][left] = dp[i-1][left]     ( j < w[i] )

dp[i][left] = max(dp[i-1][left], dp[i-1][ left-volume[i] ]+value[i] )    ( j >= w[i] )

这些代码会给人造成一种假象：dp问题的递推方向（1-n或n-1，0-v或v-0）是可以任意选取的。其实并不是这样的：对于n递推的方向，关键在于你的状态是怎样转移的。前一个代码我们的状态是从后往前转移，所以n的方向为n-1。现在这个代码就是从前往后转移（第i个物品的决策由前i-1个物品的决策得到），所以n的递推方向是1-n。所以，得到了状态转移方程，想清楚状态是从哪个状态转移到另一个状态才能选择正确的递推方向。

 

对于这个dp数组，我们还可以进行对空间的优化，变成一维数组的形式：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn = 1005;
int n, v;
int value[maxn], volume[maxn];
int dp[maxn];   //记忆化数组

int main(){
    int t;
    cin >> t;
    while(t--){
        memset(dp, 0, sizeof(dp));   //每次都要记得清空数组
        cin >> n >> v;
        for(int i = 1; i <= n; i++) cin >> value[i];
        for(int i = 1; i <= n; i++) cin >> volume[i];

        
        for(int i = 1; i <= n; i++){  
            for(int left = v; left >= 0; left--){   //left一定要从V-0,要保证取得的值是从状态i-1获得的
                if(left >= volume[i]){
                    dp[left] = max(dp[left], dp[left-volume[i]]+value[i]);
                }
            }
        }

        cout << dp[v] << endl;
    }
    return 0;
}

尤其要注意的是：这里的dp[left] = max(dp[left]，dp[left-volume[i] ] + value[i] ) 并不是状态转移方程。这个一维数组的优化刚开始我也是一头雾水，但是理解了dp后就渐渐明白了一点（太渣了/(ㄒoㄒ)/~~）。其实这个一维数组存的是前一个状态（第i-1个）的决策结果。有些人可能会问，更新了之后是第i个状态的结果，那么没被更新的怎么办？其实这个问题很好解决，看这个状态方程就行了：

dp[i][left] = dp[i-1][left]     ( j < w[i] )

或者dp[i][left] = dp[i-1][left]      ( j >= w[i] )    //也就是上面第三个状态转移方程不选的情况

没被更新就不用修改就会变成第i个状态的结果了。

当从V-0更新完时，整个数组就是第V个状态的决策结果了。最好自己在纸上模拟一下，这里就不展示了。

不过一维数组的缺点就是：搞不懂的话很容易弄错（循环方向），所以建议完全理解一维数组的原理后再进行使用效果会更佳（最好不要照搬模板和递推式）。逆向不过来的同学可以尝试这个代码（循环部分不一样外其他都一样）：

for(int i = 1; i <= n; i++){
    for(int left = v; left >= 0; left--){   //left一定要从V-0,要保证取得的值是从状态i-1获得的
        if(left + volume[i] <= v){
            dp[left+volume[i]] = max(dp[left+volume[i]], dp[left]+value[i]);
        }
    }
}

其实会发现它们的本质是一样的。