HanLP 关键词提取算法分析
HanLP 关键词提取算法分析
- 参考论文:《TextRank: Bringing Order into Texts》
- TextRank算法提取关键词的Java实现
- TextRank算法自动摘要的Java实现这篇文章中作者大概解释了一下TextRank公式
1. 论文
In this paper, we introduce the TextRank graphbased ranking model for graphs extracted from natural
language texts
TextRank是一个非监督学习算法,它将文本中构造成一个图,将文本中感兴趣的东西(比如分词)当成一个个顶点,然后应用TextRank算法来抽取文本中的一些信息。
Such keywords may constitute useful entries for building an automatic index for a document collection, can be used to classify a text, or may serve as a concise summary for a given document.
提取出来的关键词,可用来作为文本分类,或者概括文本的中心思想。
TextRank通过不断地迭代来提取关键词,每一轮迭代,算法给图中的顶点打分。直到满足某个条件(比如说迭代次数克到200次,或者设置的某个参数达到一个阈值)为止。
For loosely connected graphs, with the number of edges proportional with the number of vertices,
undirected graphs tend to have more gradual convergence curves.
对于稀疏图而言,边的数目与顶点的数目成线性关系,对这样的图进行关键词提取,有着更平缓的收敛曲线(或者叫收敛得慢吧)
It may be therefore useful to indicate and incorporate into the model the “strength”
of the connection between two vertices \(V_i\) and \(V_j\) as a weight \(w_{ij}\) added to the corresponding edge that connects the two vertices.
有时,图中顶点之间的关系并不完全平等,比如某些顶点之间关系密切,这里可用边的权重来衡量顶点之间的相关性重要程度,而这就是带权图模型。
2. 源码实现
2.1 关键词提取流程
给定若干个句子,提取关键词。而TextRank算法是 graphbased ranking model,因此需要构造一个图,要想构造图,就需要确定图中的顶点如何构造,于是就把句子进行分词,将分得的每个词作为图中的顶点。
在选取某个词作为图的顶点的时候,可以应用一些过滤规则:比如说,去除掉分词结果中的停用词、根据词性来添加顶点(比如只将名词和动词作为图的顶点)……
The vertices added to the graph can be restricted with syntactic filters, which select only lexical units of a certain part of speech. One can for instance consider only nouns and verbs for addition to the graph, and consequently draw potential edges based only on relations that can be established between nouns and verbs.
在确定好哪些词作为图的顶点之后,另一个是确定词与词之间的关系,也即:图中的哪些顶点有边?比如说设置一个窗口大小,落在这个窗口内的词,都添加一条边。
it is the application that dictates the type of relations that are used to draw connections between any two such vertices,
确定了边的关系后,接下来是确定边上权值。这个也是根据实际情况而定。
2.2 根据窗口大小确定词的邻接点
前面提到,若干句话分词之后,得到的一个个的词,或者叫Term。假设窗口大小为5。解释一下TextRank算法提取关键词的Java实现文章中提到的如何确定某个Term有哪些邻接Term。
比如说:'程序员' 这个Term,它在多个句子中出现了,因此分词结果'程序员' 出现在四个地方:
索引0处:'程序员'的邻接点有:
英文、programmer、从事、程序
索引9处:'程序员'的邻接点有:
开发、维护、专业、人员、分为、程序、设计、人员
索引26处,'程序员'的邻接点有:
中国、软件、从业人员、分为、高级、程序员、系统分析员、项目经理
索引28处,'程序员'的邻接点有:
从业人员、分为、程序员、高级、系统分析员、项目经理、四大
结合这四处窗口中的所有的词,得到'程序员'的邻接点如下:
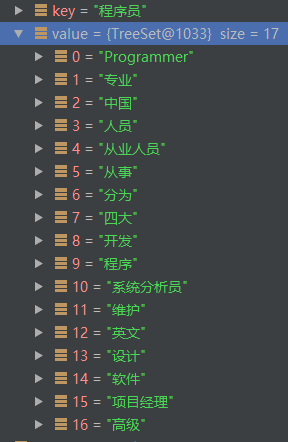
因此,当窗口大小设置为5时,Term的前后四个Term都将视为它的邻接点,并且当这个Term出现多次时,则是将它各次出现位置处的前后4个Term合并,最终作为这个Term的邻接点。
从这里可看出:如果某个Term在句子中出现了多次,意味着该Term会比较重要。因为它的邻接点会比较多,也即有很多其他Term给它投了票。这就有点类似于Term Frequency来衡量Term的重要性。
2.3 得分(score)的更新算法
m.put(key, m.get(key) + d / size * (score.get(element) == null ? 0 : score.get(element)));代码的解读:
m.get(key)如果是第一次进入for (String element : value),则是拿到公式前半部分1-d的结果;如果是已经在for (String element : value)进行了迭代,for循环相当于求和:\(\Sigma_{v_j\in In(v_i)}\)
for (String element : value) {
int size = words.get(element).size();
m.put(key, m.get(key) + d / size * (score.get(element) == null ? 0 : score.get(element)));
}
以”他说的确实在理“ 举例来说:,选取窗口大小为5,经过分词并去除停用词后:

构造的无向图如下:(每条边的权值都为1)
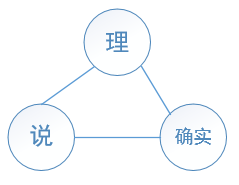
以顶点'理'为例,来看一下'理'的得分是如何被更新的。在for (String element : value)一共有两个顶点对 '理'进行投票,首先是 '确实'顶点,与'确实'顶点邻接的顶点有两个,因此:int size = words.get(element).size();中size=2。接下来,来分解一下这行代码:
m.put(key, m.get(key) + d / size * (score.get(element) == null ? 0 : score.get(element)))
-
m.get(key)为1-d,因为在外层for循环中,m.put(key, 1 - d)已经公式的前半分部(1-d)存储了。 -
score.get(element) == null ? 0 : score.get(element)这个是获取上一轮迭代的结果。对于初始第一轮迭代而言,score.get(element)为0.8807971,这个值是每个顶点的得分初始值:
//依据TF来设置初值, words 代表的是 一张 无向图
for (Map.Entry<String, Set<String>> entry : words.entrySet()) {
score.put(entry.getKey(), sigMoid(entry.getValue().size()));//无向图的每个顶点 得分值 初始化
}
score.get(element)相当于公式中的\(WS(V_j)\)
-
最后来分析一个 size,size是由代码
int size = words.get(element).size()获得的,由于每条边权值为1,size其实相当于:\(\Sigma_{V_k\in Out(V_j)}w_{jk}\)。In('理')=
-
当\(V_j\)为'确实'时,\(Out(V_j)\)为{'说','理'},因此:\(\Sigma_{V_k\in Out(V_j)}w_{jk}=2\)。于是,更新顶点'理'的得分:\(1-d+d*(1/2)*0.8807971=0.5243387\)。然后再通过m.put将临时结果保存起来。
-
接下来,
for (String element : value)继续,此时:\(V_j\)为顶点'说',由于顶点'说'也有两条邻接边,因此有:\(\Sigma_{V_k\in Out(V_j)}w_{jk}=2\)。于是更新顶点'理'的得分:\(0.5243387+d*(1/2)*0.8807971=0.89867747\)。而这就是第一轮迭代时,顶点'理'的得分。根据上面的1、2中的步骤,
for (String element : value)就相当于:\(\Sigma_{V_j\in In(V_i)}\),因为每次都把计算好的结果再put回HashMap m中。
因此,在第一轮迭代中,顶点'理'的得分就是:0.89867747
类似于,经过:max_iter次迭代,或者达到阈值:
-
if (max_diff <= min_diff)
break;
时,就不再迭代了。
下面再来对代码作个总体说明:
这里是构造无向图的过程
for (String w : wordList) {
if (!words.containsKey(w)) {
//排除了 wordList 中的重复term, 对每个已去重的term, 用 TreeSet<String> 保存该term的邻接顶点
words.put(w, new TreeSet<String>());
}
// 复杂度O(n-1)
if (que.size() >= 5) {
//窗口的大小为5,是写死的. 对于一个term_A而言, 它的前4个term、后4个term 都属于term_A的邻接点
que.poll();
}
for (String qWord : que) {
if (w.equals(qWord)) {
continue;
}
//既然是邻居,那么关系是相互的,遍历一遍即可
words.get(w).add(qWord);
words.get(qWord).add(w);
}
que.offer(w);
}
这里是对图中每个顶点赋值一个初始score过程:
Map<String, Float> score = new HashMap<String, Float>();//保存最终每个关键词的得分
//依据TF来设置初值, words 代表的是 一张 无向图
for (Map.Entry<String, Set<String>> entry : words.entrySet()) {
score.put(entry.getKey(), sigMoid(entry.getValue().size()));//无向图的每个顶点 得分值 初始化
}
接下来,三个for循环:第一个for循环代表迭代次数;第二个for循环代表:对无向图中每一个顶点计算得分;第三个for循环代表:对某个具体的顶点而言,计算它的每个邻接点给它的投票权重。
for (int i = 0; i < max_iter; ++i) {
//....
for (Map.Entry<String, Set<String>> entry : words.entrySet()) {
//...
for (String element : value) {
这样,就实现了论文中公式:
而最终提取出来的关键词是:
[理, 确实, 说]
上面只是用 ”他说的确实在理“ 这句话 演示了TextRank算法的具体细节,在实际应用中可能不合理。因为会存在:
- 现有统计信息不足以让TextRank支持 某个词 的重要性,算法有局限性。
可见:TextRank提取关键词是受到分词结果的影响的;其次,也受窗口大小的影响。虽然说代码是大致看懂了,但是还是有一些疑问的:比如,为什么用上面那个公式计算,得分高的词语就是关键词了?根据TextRank求关键词与Term Frequency求关键词有什么优势?选取文本中的哪些词建立模型作为图的顶点?基于文本之间的什么样的关系作为图的边?



 浙公网安备 33010602011771号
浙公网安备 33010602011771号