贝叶斯推断之拉普拉斯近似
贝叶斯推断之拉普拉斯近似
本文介绍使用拉普拉斯近似方法来求解贝叶斯后验概率分布。在上一篇文章：贝叶斯推断之最大后验概率(MAP)中介绍了使用点估计法来求解后验概率分布，在文章中定义了后验概率分布公式:
分母\(p(t|X)\)是与参数 \(w\)无关，可视为常量。
定义函数\(g\)如下：
因此，\(g\)与\(p(w|t,X)\)之比为常数。上文介绍了点估计法求解\(p(w|t,X)\)。本文介绍拉普拉斯近似法求解\(p(w|t,X)\)。
什么是拉普拉斯近似？
由于没法直接求解\(p(w|t,X)\)，转而求解\(g(w;X,t,\sigma^2)\)，拉普拉斯近似就是首先假设函数\(log(g(w;X,t,\sigma^2))\)服从高斯分布，然后通过泰勒展开公式，将\(log(g(w;X,t,\sigma^2))\)在\(w^*\)处展开。 \(w^*\)就是上文使用牛顿法求得的最优参数。
高斯分布的数学表达式如下：
若知道了均值\(u\)和方差\(\sigma^2\)，也就求得了\(g\)的高斯分布形式。
泰勒展开
根据上文介绍在\(w^*\)处，\(log(g(w;X,t,\sigma^2))\)的一阶导数等于0，二阶导数小于0（对于多元函数，则是黑赛矩阵负定）。因此，对它进行二阶泰勒展开如下：
由于一阶导数为0，化简为：
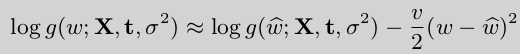
公式(1)
其中，\(v\)如下：
对高斯分布的数学表达式取对数：
其中，\(K=\frac{1}{\sqrt{2\pi}}\)是一个常数。对比公式1 \(log(g(w;X,t,\sigma^2))\) 和 公式2，求得高斯分布参数：
\(u=w^*\)
\(\sigma^2=\frac{1}{v}\)
至此，我们就求解出了函数\(log(g(w;X,t,\sigma^2))\)的高斯分布，而\(g\)与\(p(w|t,X)\)之比为常数，也就求得了后验概率\(p(w|t,X)\)的分布了。
使用后验概率分布的期望值进行预测
对于一个新样本\(x_{new}\)，将它归为负类的概率为：\(P(T_{new}=1|x_{new},X,t,\sigma^2)\)
而这个概率就是计算： \(p(w|t,X)\)所服从的分布的期望。 为什么是计算 期望呢？因为参数\(w\)不是单个具体的值了，而是一个随机变量了，\(w\)的函数服从高斯分布。而期望的数学意义是“平均”，因此将期望值作为“归类为负类的概率”更准确（capture more uncertainty）
通过前面的拉普拉斯近似，我们知道它服从正态分布：
\(p(w|t,X)\)~\(N(u,\sigma^2)\)
若\(w\)是对于多元变量，则
\(p(w|t,X)\)~\(N(u, \Sigma)\)，其中\(u\)是个向量，\(\Sigma\)是个矩阵
故：
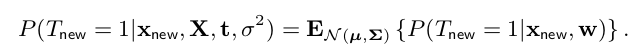
高斯分布是个连接型随机变量的分布，因此求解高斯分布的期望值，就是对概率密度函数进行积分，显然概率密度函数是个关于\(w\)的函数，然而由于：
对\(w\)的积分值无法计算出来，即无法求解出：\(E_{N(u,\Sigma)}(P(T_{new}=1|x_{new},w))\)
幸运的是，我们求解的是高斯分布的期望值，于是选取 \(N_s\)个样本来近似计算期望值：
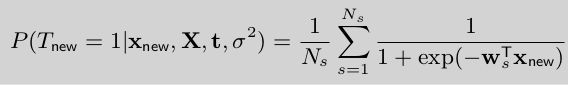
从而，求得了预测概率。至此，使用拉普拉斯近似法 求解 后验概率分布就介绍完毕了。
decision boundary
点估计法求解出来的后验概率是一个具体的关于\(w\)的函数，而拉普拉斯近似法求解出来的后验概率是一个服从高斯分布的随机变量。
在点估计法中，decision boundary是一条条的直线，而由于随机变量的不确定性，拉普拉斯近似法得出的decision boundary有很多是弯曲的：
总结
拉普拉斯近似法是计算后验概率的另一种方法。它首先假设后验概率\(p(w|t,X)\) 服从高斯分布。然后，将与后验概率\(p(w|t,X)\) 相比为常数的 函数 \(g(w;X,t,\sigma^2)\) 的log形式 在 \(w^*\)处进行泰勒展开，从而求解出这个高斯分布。
\(w^*\)则是通过上文中提到的牛顿法求解出来的。
有了这个高斯分布之后，对于每一个新样本，计算该高斯分布的期望值，就是模型对这个新样本的预测值。
