感知机的简单理解
一，感知机模型
1，超平面的定义
令w1，w2，...wn，v都是实数(R) ，其中至少有一个wi不为零，由所有满足线性方程w1*x1+w2*x2+...+wn*xn=v
的点X=[x1,x2,...xn]组成的集合，称为空间R的超平面。
从定义可以看出：超平面就是点的集合。集合中的某一点X，与向量w=[w1，w2，...wn]的内积，等于v
特殊地，如果令v等于0，对于训练集中某个点X：
w*X=w1*x1+w2*x2+...+wn*xn>0，将X标记为一类
w*X=w1*x1+w2*x2+...+wn*xn<0，将X标记为另一类
2，数据集的线性可分
对于数据集T={(X1, y1),(X2, y2)...(XN, yN)}，Xi belongs to Rn，yi belongs to {-1, 1}，i=1,2,...N
若存在某个超平面S：w*X=0
将数据集中的所有样本点正确地分类，则称数据集T线性可分。
所谓正确地分类，就是：如果w*Xi>0，那么样本点(Xi, yi)中的 yi 等于1
如果w*Xi<0，那么样本点(Xi, yi)中的 yi 等于-1
因此，给定超平面 w*X=0，对于数据集 T中任何一个点(Xi, yi)，都有yi(w*Xi)>0，这样T中所有的样本点都被正确地分类了。
如果有某个点(Xi, yi)，使得yi(w*Xi)<0，则称超平面w*X对该点分类失败，这个点就是一个误分类的点。
3，感知机模型
f(X)=sign(w*X+b)，其中sign是符号函数。
感知机模型，对应着一个超平面w*X+b=0，这个超平面的参数是(w,b)，w是超平面的法向量，b是超平面的截距。
我们的目标是，找到一个(w,b)，能够将线性可分的数据集T中的所有的样本点正确地分成两类。
如何找到(w,b)？---感知机学习算法做的事
二，感知机学习算法
既然我们的目标是将T中所有的样本点正确地分类，那么对于某个(w,b)，先看一下它在哪些点上分类失败了。由前面所述：
如果有某个点(Xi, yi)，使得yi(w*Xi)<0，则称超平面w*X对该点分类失败。采用所有误分类的点到超平面的距离来衡量分类失败的程度。
n维空间Rn中一点Xi到超平面w*X+b=0的距离公式：
，可参考点到平面的距离公式。
对于误分类的点，有yi(w*Xi)<0。而距离总是大于0的，因此，某个误分类的点到超平面的距离表示为：
||w||是一个常数，对最小化L(w,b)没有影响，故忽略之。
假设所有的误分类点都在集合M中，得到的损失函数如下：
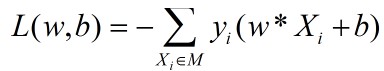
最终，将寻找(w,b)问题转化为最小化损失函数，即转化为一个最优化问题。（损失函数越小，说明误分类的样本点“越少”---或者说分类失败的程度越低）
而这个优化问题可以用梯度下降法来寻找最优的(w,b)
1，为什么使用梯度下降？(没有解析解，用数值解来求解)
minL(w,b)没有 analytical solution，我的理解是：不能通过数学公式各种推导，最终求得一个关于最优的w 和 b 的解。比如，Stanford CS229课程中cs229-notes1.pdf 中求解 linear regression 的代价函数J(θ)的参数θ，可以使用Normal Equation 方法：直接根据公式得到θ
Gradient descent gives one way of minimizing J. Let’s discuss a second way of doing so,
this time performing the minimization explicitly and without resorting to an iterative algorithm.
上面说的second way of doing so. second way就是Normal Equation方法
梯度下降，则是一种迭代算法，使用不断迭代(w,b)的方式，使得L(w,b)变得越来越小。
另外一个原因是（不知道对不对）：在《机器学习基石》视频中讲到NP-Hard问题。
x
梯度方向是函数L(w,b)增加最快的方向，而现在要最小化L(w,b)，在当前的(w,b)点，从梯度的负方向搜索下一个(w,b)点，那么找到的(w,b)就是使L(w,b)减少的最快的方向上的那个点(还与搜索的步长有关)了。
现在证明为什么梯度方向是函数f(x)增加最快的方向，这里涉及到几个概念：
①梯度
梯度是个向量，由于x=[x1,x2,...xn]是n维的，梯度就是对x的各个分量xi求偏导数：
②增加的方向---方向导数
给定一个函数f(x)，通俗地讲方向导数就是决定 自变量x 可以往哪个方向移动。比如在f(x)边界上，x往某个方向移动时，就不在定义域的范围内了，那x是不能往该方向变化的。假设 d 是f(x)的一个可行方向，||d||=1，那么函数f 的值在 x 处 沿着方向d 的增长率increase_rate，可以用内积表示：
那么现在，到底往哪个方向增长，能够使 increase_rate 最大呢？也即，d取哪个方向，使 increase_rate 最大？
根据柯西-施瓦兹不等式有：(后面算法的收敛性证明也会用到)
也就是说，increase_rate的最大值为：
而当 d =
时，根据内积的定义：
increase_rate等于：
此时，increase_rate取最大值，且可行方向d 就是梯度方向！
因此，若要最小化L(w,b)，往梯度的负方向搜索(w,b)，能使L(w,b)下降得最快。
根据前面的介绍，梯度实际上是求偏导数，因此L(w,b)分别对w 和 b 求偏导数：
而在感知机中是一次只选择一个误分类点对(w,b)进行迭代更新，选择梯度的负方向进行更新，故更新的公式如下所示：
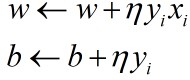
三，感知机学习算法的收敛性证明
由于数据集T是线性可分的，假设存在一个理想的超平面wopt，且||wopt||=1，wopt能够将T中的所有样本点正确地分类。
如前所述，若正确分类，则对于数据集 T中任何一个点(Xi, yi)，都有yi(w*Xi)>0
取r=min{yi(wopt*Xi)} ，并且令R=max||xi|| ，则迭代次数k满足下列不等式：
具体证明过程见《统计学习方法》p32-p33页
在证明过程中，推导出了两个不等式，一个是：wk*wopt >= knr (k是迭代次数，n是迭代步长，r是min{yi(wopt*Xi))
超平面wopt是理想的超平面，能够完美地将所有的样本点正确地分开。wk是采用感知机学习算法使用梯度下降不断迭代求解的超平面，二者之间的内积，用来衡量这两个超平面的接近程度。因为两个向量的内积越大，说明这两个向量越相似(接近),也就是说:不断迭代后的wk越来越接近理想的超平面wopt了。（向量的模为1，||wopt||=1）
第二个不等式是：
结合上面的二个不等式，有：
其中第一个不等号成立是因为：wk*wopt >= knr
第二个不等号成立是因为：柯西-施瓦兹不等式
第三个不等号成立是因为：第二个不等式 和 ||wopt||=1
四，参考文献
《统计学习方法》
《最优化导论》
原文：http://www.cnblogs.com/hapjin/p/6714526.html
