【OI向】初赛题目选讲
【OI向】初赛题目选讲
声明
- 如果不作特殊说明,本文中出现的所有 \(\log\) 都是指以二为底的对数。
- 本文的讨论范围对读者的程序设计能力不作要求,即基本不存在程序阅读和程序填空。
- 本文所讲的都是历年真题,题目的顺序按年份排列。
1.组合数学
本节内容是提高组的常考题型,且考察的通常为经典题和简单题,部分题目也可以通过暴力枚举来完成。
1.1
(NOIP2007提高组) 给定 \(n\) 个有标号的球,标号依次为 \(1,2,\cdots,n\) 。将这 \(n\) 个球放入 \(r\) 个相同的盒子里,不允许有空盒,其不同放置方法的总数记为 \(S(n,r)\) 。例如, \(S(4,2)=7\) ,这 \(7\) 种不同的放置方法依次为 \(\left \{ (1),(234) \right \} ,\left \{ (2),(134)) \right \} ,\left \{ (3),(124)\right \} ,\left \{(4),(123)\right \} ,\left \{(12),(34)\right \} ,\left \{(13),(24)\right \} , \left \{(14),(23)\right \}\) 。当 \(n=7,r=4\) 时, \(S(7,4)\) 为?
\(S(n,r)\) 通常称为第二类斯特林数。这里直接给出递推公式。其推导,读者可以自行了解。
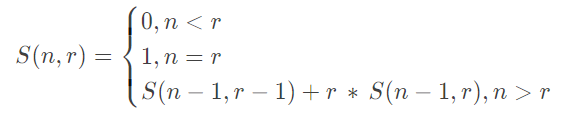
根据公式,易得本题答案为 \(350\) 。
1.2
(NOIP2008普及组)书架上有 \(4\) 本不同的书 \(A,B,C,D\) 。其中 \(A\) 和 \(B\) 是红皮的, \(C\) 和 \(D\) 是黑皮的。把这 \(4\) 本书摆在书架上,满足所有黑皮的书都排在一起的摆法有几种?满足 \(A\) 必须比 \(C\) 靠左,所有红皮的书要摆放在 一起,所有黑皮的书要摆放在一起,共有几种摆法?
第一问:把 \(C,D\) 看作一个整体,原题成了求 \(A_{3}^{3}\) ,然后乘上 \(C,D\) 的全排列,答案为 \(A_{3}^{3}\times A_{2}^{2}=12\) 种。
第二问: 在上一题的基础上把 \(A,B\) 看作一个整体, \(A,B\) 和 \(C,D\) 分别全排列。又由题意,\(A,B\) 一定在 \(C,D\) 左。因此答案为 \(A_{2}^{2}\times A_{2}^{2}=4\) 种。
1.3
(NOIP2008提高组) 书架上有 \(21\) 本书,编号从 \(1\) 到 \(21\) ,从其中选 \(4\) 本,其中每两本的编号都不相邻的选法一共有几种?
对于相邻的选法,可以先不考虑不相邻元素的排法,而是先将余下的元素排好,然后将需要不相邻的元素在已排好元素间插空。
考虑剩下的 \(17\) 本会留下 \(18\) 个空,显然选出的 \(4\) 本会插入到这 \(18\) 个空里。然后考虑选的 \(4\) 本肯定是个组合,不是排列。那么问题就转化成了 \(18\) 个空里插入 \(4\) 本书的方案数,即为 \(C_{18}^{4}=3060\) 种。
推广: \(n\) 个元素中有 \(m\) 个元素不相邻的放法有 \(C_{n-m+1}^{m}\) 种。
1.4
(NOIP2009普及组)小陈现有 \(2\) 个任务 \(A,B\) 要完成,每个任务分别有若干步骤如下:\(A=a_1\to a_2\to a_3,B=b_1\to b_2\to b_3\to b_4\to b_5\) 。在任何时候,小陈只能专心做某个任务的一个步骤。但是如果愿意,他可以在做完手中任务的当前步骤后,切换至另一个任务,从上次此任务第一个未做的步骤继续。每个任务的步骤顺序不能打乱,例如 \(\dots a_2\to b_2\to a_3\to b_3 \dots\) 是合法的,而 \(\dots a_2\to b_3\to a_3\to b_2\dots\) 是不合法的。小陈从 \(B\) 任务的 \(b_1\) 步骤开始做,当恰做完某个任务的某个步骤后,就停工回家吃饭了。当他回来时,只记得自己已经完成了整个任务 \(A\) ,其他的都忘了。试计算小陈饭前已做的可能的任务步骤序列共有几种?
\(5\) 种情况,没完成,完成 \(b_1\) ,完成 \(b_1,b_2\) ,…,完成 \(b_1,\dots,b_4\) 。然后我们将每种情况所有完成的序列组成一个集合。
设有 \(k\) 个元素,其中有 \(l\) 个元素属于 \(b\),那么我们就是在这个集合里选取 \(l\) 个位置放给 \(b\) 中的元素,剩下的 \(a\) 位置就唯一确定,因此答案为 \(C_3^0 + C_4^1 + C_5^2 + C_6^3 + C_7^4 = 70\) 。
1.5
(NOIP2011普及组) 每份考卷都有一个 \(8\) 位二进制序列号。当且仅当一个序列号含有偶数个 \(1\) 时,它才是有效的。例如,\(00000000,01010011\) 都是有效的序列号,而 \(11111110\) 不是。那么,有效的序列号共有几个?
总共有 \(2^8=256\) 个序列,其中要么含有偶数个 \(1\) ,要奇数个,所以对半分为 \(128\) 个。
1.6
(NOIP2012普及组) 在 NOI 期间,主办单位为了欢迎来自各国的选手,举行了盛大的晚宴。在第 十八桌,有 \(5\) 名大陆选手和 \(5\) 名港澳选手共同进膳。 为了增进交流, 他们决定相隔就坐,即每个大陆选手左右旁都是港澳选手,每个港澳选手左右旁都是大陆选手。那么,这一桌一共有几种不同的就坐方案?注:如果在两个方案中,每个选手左右相邻的选手相同 ,则视为同一种方案。
解法一:
显然是先确定大陆,因为是环所以不需要讨论第一个位置选不选,那么 \(5\) 个位置 \(5\) 个人的排列,加上环的问题,就是 \(\frac{A_5^5}{5}\),然后用乘法原理乘下港澳选手的方案数,此时不需要考虑环了。答案是\(\frac{5!^2}{5} = 2880\) 。
解法二:
如果一个题是环/树的太难,我们把它放在链上考虑。链上就需要考虑大陆选手是 \(1,3,5,7,9\) 还是 \(2,4,6,8,10\) 了,那么链上的方法数是 \(2\times(A_5^5)^2\),然后考虑环的形式,显然除以 \(10\) ,即 \(\frac{28800}{10}= 2880\),同样也是答案。
1.7
(NOIP2014提高组) 由数字 \(1,1,2,4,8,8\) 所组成的不同的四位数的个数为?
对于这类题,我们进行分类讨论即可。
- 没有重复的情况,显然为 \(1,2,4,8\) 的全排列,即 \(A_{4}^{4}=24\) 。
- 有一对重复的情况,首先我们在 \(1,8\) 中挑选一个,然后除去已选的 \(2\) 个 \(1\) 或 \(2\) 个 \(8\) ,剩下的还有 \(3\) 种可能。先进行全排列,再除以重复计数的部分,即 \(\frac{A_{4}^{4}\times C_{2}^{1}\times C_{3}^{2}}{A_{2}^{2}}=72\) 。
- 有两对重复的情况,显然只有 \(1,1,8,8\) 的全排列,然后再除以重复计数的部分,即 \(\frac{A_{4}^{4}}{A_{2}^{2}\times A_{2}^{2}}=6\) 。
故,我们将三种情况加起来就可以得到本题的答案 \(102\) 。
1.8
(NOIP2015普及组) 重新排列 \(1234\) 使得每一个数字都不在原来的位置上,一共有几种排法?
这类题我们称之为错排问题,这类题有一个公式,我们来讲讲公式的推导。
第一步,把 \(n\left ( n\ge 2\right )\) 个元素放在一个位置上,比如 \(k\) ,一共有 \(n-1\) 种方法。
第二步,放编号为 \(k\) 的元素,这是有两种情况:
$\left ( 1\right ) $ 把它放到位置 \(n\) ,那么,对于剩下的 \(n-1\) 个元素,由于第 \(k\) 个元素放到了位置 \(n\) ,剩下 \(n-2\) 个元素就有 \(D\left ( n-2\right )\) 种方法
\(\left ( 2\right )\) 第 \(k\) 个元素不把它放到位置 \(n\) ,这时,对于这 \(n-1\) 个元素,有 \(D\left ( n-1\right )\) 种方法,所以递推公式为 \(D\left ( n\right ) =\left ( n-1\right )*\left [D \left ( n-1\right )+D\left ( n-2\right ) \right ]\) 。其中,初始值 \(D\left (1\right )=0\) , \(D\left (2\right )=1\) 。
根据公式,我们易得答案为 \(9\) 。
1.9
(CSP-J 2019) 一些数字可以颠倒过来看,例如 \(0,1,8\) 颠倒过来还是本身,\(6\) 颠倒过来是 \(9\) ,\(9\) 颠倒过来看还是 \(6\) ,其他数字颠倒过来都不构成数字。类似的,一些多位数也可以颠倒过来看,比如 \(106\) 颠倒过来是 \(901\) 。假设某个城市的车牌只由 \(5\) 位数字组成,每一位都可以取 \(0\) 到 \(9\) 。请问这个城市最多有多少个车牌倒过来恰好还是原来的车牌?
先考虑中间一位,显然只能选 \(0,1,8\) ,因此答案是 \(3\) 乘以 \(1,2,4,5\) 位的方案,我们发现一旦 \(1,2\) 位确定,则 \(4,5\) 位的选法是唯一确定的,因此答案是 \(5\times5\times3 = 75\) 。
我们再加上一个限制条件,即” 车牌上的 5 位数能被 3 整除 ”,这也正是同年提高组初赛的一道选择题。
在原先的基础上,我们发现, \(0,1,8\) 模 \(3\) 正好为 \(0,1,2\) ,所以在给定其他 \(4\) 位的情况下,第 \(3\) 位有且仅有 \(1\) 种选择,因此答案是 \(5\times5 = 25\) 。
2.概率与期望
本节内容是提高组的较常考题型,也较有难度。
2.1
(NOIP2013提高组)现有一只青蛙,初始时在 \(n\) 号荷叶上。当它某一时刻在 \(k\) 号荷叶上时,下一时刻将等概率地随机跳到 \(1,2,\cdots, k\) 号荷叶之一上,直至跳到 \(1\) 号荷叶为止。当 \(n=2\) 时,平均一 共跳 \(2\) 次;当 \(n=3\) 时,平均一共跳 \(2.5\) 次。则当 \(n=5\) 时,平均一共跳几次?
设 \(f(i)\) 为期望要跳 \(i\) 次到达 \(1\) 号点,显然 \(f(1)=0\) 。
有 \(\frac{1}{5}\) 的概率跳到 \(1\) ,花费 \(1+f(1)\) 。
有 \(\frac{1}{5}\) 的概率跳到 \(2\) ,花费 \(1+f(2)\) 。
\(\cdots\)
有 \(\frac{1}{5}\) 的概率跳到 \(5\) ,花费 \(1+f(5)\) 。
加一是因为又多跳了一步,那么我们推广一下。
\(\begin{align*} f(k)&=\frac{1}{k}\sum_{i=1}^{k}(f(i)+1) \end{align*}\)
那么我们递推即可得到 \(f(5)=\frac{37}{12}\) 。
当然,对于上式,读者若有兴趣也可以自行化简一下。
2.2
(NOIP2017提高组)小明要去南美洲旅游,一共乘坐三趟航班才能到达目的地,其中第 \(1\) 个航班准点的概率是 \(0.9\) ,第 \(2\) 个航班准点的概率为 \(0.8\) ,第3个航班准点的概率为 \(0.9\) 。如果存在第 \(i\) 个 \((i=1,2)\) 航班晚点,第 \(i+1\) 个航班准点,则小明将赶不上第 \(i+1\) 个航班,旅行失败;除了这种情况,其他情况下旅行都能成功。请问小明此次旅行成功的概率是?
本题较简单,大家可以自己试一试。
我们统计各种情况的概率,然后加起来,也可以采用扣除法。
\(1-(0.1\times0.8)-(0.2\times0.9)=0.74\) 。
2.3
(NOIP2018提高组)在一条长度为 \(1\) 的线段上随机取两个点,则以这两个点为端点的线段的期望长度是?
由于本题存在一定难度,故给出多个可以做出本题的方法,读者自行选择最适合自己的一种。
解法一:
我们先考虑固定一个端点的情况,如果左端点固定在了最左边,那么答案为 \(\frac{1}{2}\) ,既然左端点更大,那么看到答案会小于 \(\frac{1}{2}\) 。在原题中仅有 \(\frac{1}{3}\) 这一个选项满足条件,则可得出答案。
解法二:
如图,我们设第一个点坐标为 \(x\) ,则与它的期望距离为 \(\frac{x\times x+(1-x)\times(1-x)}{2\times1}=x^2-x+\frac{1}{2}\) 。
由于 \(x\in [0,1]\) ,则两点的期望距离为 \(\int_{0}^{1}(x^2-x+\frac{1}{2})dx=\frac{1}{3}\) 。
解法三:
假设可以把这条线段分成 \(n\) 段,每段的长度是 \(\frac{1}{n}\) ,我们定义 \(ans\) 即为答案。
\(\begin{align*} ans&=\frac{\sum_{i=1}^{n}\sum_{j=1}^{n}\frac{j-i}{n}}{n(n+1)\times\frac{1}{2}}\\ &=\frac{\sum_{i=1}^{n}(1+n-i)\times(n-i)\times\frac{1}{2}}{n^2(n+1)\times\frac{1}{2}}\\ &=\frac{\sum_{i=1}^{n}n+n^2-2in-i+i^2}{n^2(n+1)}\\ &=\frac{n^2+n^3-(2n+1)\sum_{i=1}^{n}i+\sum_{j=1}^{n}j^2}{n^2(n+1)}\\ &=\frac{n^2(n+1)-n(n+1)(2n+1)\times\frac{1}{2}+n(n+1)(2n+1)\times\frac{1}{6}}{n^2(n+1)}\\ &=\frac{n^2(n+1)-n(n+1)(2n+1)\times\frac{1}{3}}{n^2(n+1)}\\ &=1-\frac{2n+1}{3n} \end{align*}\)
当 \(n\) 趋向于正无穷时, \(ans=\frac{1}{3}\) 。
解法四:
我们设长度为 \(x\) 的线段答案是 \(f(x)\) ,那么显然有 \(f(x)=2f(\frac{x}{2})\) 。
考虑分类讨论:
第一种情况:两个点都在 \([0,\frac{x}{2}]\) ,概率为 \(\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}\) ,期望长度为 \(f(\frac{x}{2})\) ,故对答案的贡献为 \(\frac{f(\frac{x}{2})}{4}=\frac{f(x)}{8}\) 。
第二种情况:两个点都在 \((\frac{x}{2},x]\) ,与上面一种情况同理,对答案的贡献为 \(\frac{f(x)}{8}\) 。
第三种情况:第一个点在 \([0,\frac{x}{2}]\) ,第二个点在 \((\frac{x}{2},x]\) ,概率为 \(\frac{1}{4}\) ,第一个点到 \(\frac{x}{2}\) 的期望长度是 \(\frac{x}{4}\) ,第二个点同理,到 \(\frac{x}{2}\) 的期望长度也是 \(\frac{x}{4}\) ,对答案的贡献为 \(\frac{1}{4}\times(\frac{x}{4}+\frac{x}{4})=\frac{x}{8}\) 。
第四种情况:第一个点在 \((\frac{x}{2},x]\) ,第二个点在 \([0,\frac{x}{2}]\) ,与上一种情况同理,对答案的贡献为 \(\frac{x}{8}\) 。
故有方程: \(f(x)=\frac{f(x)}{8}+\frac{f(x)}{8}+\frac{x}{8}+\frac{x}{8}\) 。
解得 \(f(x)=\frac{x}{3}\) 。
2.4
(NOIP2018提高组) 假设一台抽奖机中有红、蓝两色的球,任意时刻按下抽奖按钮,都会等概率获得红球或蓝球之一。有足够多的人每人都用这台抽奖机抽奖,假如他们的策略均为:抽中蓝球则继续抽球,抽中红球则停止。最后每个人都把自己获得的所有球放到一个大箱子里,最终大箱子里的红球与蓝球的比例接近于?
本题亦有多种解法,读者可自行选择最适合自己的一种。
解法一:
红球每个人都会抽一个, 蓝球设每个人抽 \(S\) 个, \(n\) 趋向于正无穷。
\(\begin{align*} S&=\frac{0}{2^1} +\frac{1}{2^2}+\frac{2}{2^3}+\cdots+\frac{n-1}{2^n}\\ \frac{S}{2}&=\frac{0}{2^2} +\frac{1}{2^3}+\frac{2}{2^4}+\cdots+\frac{n-2}{2^n}+\frac{n-1}{2^{n+1}}\\ \end{align*}\)
接着,我们将两式相减。
\(\begin{align*} \frac{S}{2}&=\frac{1}{2^2} +\frac{1}{2^3}+\frac{1}{2^4}+\cdots+\frac{1}{2^n}-\frac{n-1}{2^{n+1}} \\ S&=1 \end{align*}\)
所以比例是 \(1:1\) 。
解法二:
一个人在第 \(i\) 轮可以得到的蓝球期望数量为 \(\frac{1}{2^i}\) ,而 \(\begin{align*} \sum_{i=1}^{\infty } \frac{1}{2^i} =1 \end{align*}\) ,所以每个人得到红球期望数量为 \(1\) ,而得到蓝球数量必定为 \(1\) ,所以为 \(1:1\) 。
解法三:
通俗地说,每一轮会有一半人红,一半人蓝,蓝的进入下一轮,故一直都是 \(1:1\) 。
3.时间复杂度
这节内容是提高组的常考题型,在此仅介绍递推的做法,当然也存在主定理,画递归树等做法,但这里不做详细介绍了,有余力的读者可以自行了解。
该节内容,需要读者对递归,递推,分治,对数的运算,渐进记号(以 \(\mathcal{O}\) 为主)等有基本的认识。
其中,关于对数的运算可以去看看我曾写过的一篇对数入门的blog:传送门。
3.1
(NOIP2013提高组)斐波那契数列的定义如下: \(F_1=1,F_2=1,F_n=F_{n-1}+F_{n-2}(n≥3)\) 。如果用下面的函数计算斐波那契数列的第 \(n\) 项,则其时间复杂度为?
这题其实并未涉及到计算,历年考频也较低,以此为例掌握即可。
该函数可以理解为一棵二叉树,根节点的值等于两个子节点的和,叶子节点的值为 \(1\) 。函数的最终返回值为 \(F_n\) ,因此一共有 \(F_n\) 个叶子节点,总的时间复杂度为 \(\mathcal{O}(F_n)\) 。
3.2
(NOIP2013提高组)若某算法的计算时间表示为递推关系式:
\(T(n)=2T(\frac{n}{2})+2n\)
\(T(1)=1\)
则该算法的时间复杂度为?
本题将介绍两个解法。
解法一:
题中的递归式,相当于归并排序的复杂度,每次分治成两个子问题,合并子问题的代价为 \(n\) ,我们可以想象成共有 \(\log n\) 层,每次代价总共需要 \(\mathcal{O}(n)\) 。因此总的时间复杂度为 \(\mathcal{O}(n\log n)\) 。
解法一可能有些抽象,倒不如解法二来的较为直接,也是做此类题的通法。
解法二:
\(\begin{align*} T(n) &= 2[2T(\frac{n}{4}) + 2\times\frac{n}{2}] + 2n \\ &= 4T(\frac{n}{4}) + 4n\\ &= \cdots\\ &=2^kT(\frac{n}{2^k})+2kn \end{align*}\)
我们观察怎么样才能将 \(T(\frac{n}{2^k})\) 化至 \(T(1)\) ,显然,当且仅当 \(k=\log n\) 时。
故,我们将 \(k=\log n\) 带入上式。
\(\begin{align*} T(n)&= 2^{\log n}T(1)+2\log n \times n \\ &= n+2n\log n\\ \end{align*}\)
故,总的时间复杂度为 \(\mathcal{O}(n\log n)\) 。
3.3
(NOIP2015提高组)若某算法的计算时间表示为递推关系式:
\(T(n)=T(n-1)+n\)
\(T(0)=1\)
则该算法的时间复杂度为?
实际上,本题较上题更为简单,所以就留作读者自行练习。
本题答案为: \(\mathcal{O}(n^2)\)
解析:
\(\begin{align*} T(n)&=T(n-2)+(n-1)+n\\ &=\cdots\\ &=T(0)+1+2+\cdots+n \\ &=1+\frac{n(n+1)}{2}\\ \end{align*}\)
故,总的时间复杂度为 \(\mathcal{O}(n^2)\) 。
3.4
(NOIP2016提高组)若某算法的计算时间表示为递推关系式:
\(T(n)=2T(\frac{n}{4})+\sqrt n\)
\(T(1)=1\)
则该算法的时间复杂度为?
同样地,本题也就留作读者自行练习。
本题答案为: \(\mathcal{O}(\sqrt n\log n)\)
解析:
\(\begin{align*} T(n)&=2T(\frac{n}{4})+\sqrt n\\ &=2(2T(\frac{n}{16})+\sqrt{\frac{n}{4}})+\sqrt n\\ &=4T(\frac{n}{16})+2\sqrt n\\ &=\cdots\\ &=2^kT(\frac{n}{4^k})+k\sqrt n \\ \end{align*}\)
我们观察怎么样才能将 \(T(\frac{n}{4^k})\) 化至 \(T(1)\) ,显然,当且仅当 \(k=\log_4 n\) 时。
故,我们将 \(k=\log_4 n\) 带入上式。
\(\begin{align*} T(n)&= 2^{\log_4 n}T(1)+\log_4 n \sqrt n \\ &= \sqrt n+\log_4 n\sqrt n\\ \end{align*}\)
故,总的时间复杂度为 \(\mathcal{O}(\sqrt n\log n)\) 。
3.5
(NOIP2017提高组)若某算法的计算时间表示为递推关系式:
\(T(n)=2T(\frac{n}{2})+n\log n\)
\(T(1)=1\)
则该算法的时间复杂度为?
本题前面的步骤不再赘述。
\(\begin{align*} T(n)&=2(2T(\frac{n}{4})+\frac{n}{2}\log {\frac{n}{2}})+n\log n\\ &=4T(\frac{n}{4})+n(\log\frac{n}{2}+\log n)\\ &=\cdots\\ &=2^kT(\frac{n}{2^k})+n\sum_{i=0}^{k-1} \log \frac{n}{2^i} \\ \end{align*}\)
接下来,我们来考虑这么化简上式。
\(\begin{align*} \sum_{i=0}^{k-1} \log \frac{n}{2^i}&= k\log n-(\log 2+\log4+\cdots+\log 2^{k-1}) \\ &=k\log n-\frac{k(k-1)}{2}\\ \end{align*}\)
故,上式可进一步化简。
\(\begin{align*} T(n) &=2^kT(\frac{n}{2^k})+n(k\log n-\frac{k(k-1)}{2}) \\ \end{align*}\)
我们观察怎么样才能将 \(T(\frac{n}{2^k})\) 化至 \(T(1)\) ,显然,当且仅当 \(k=\log n\) 时。
故,我们将 \(k=\log n\) 带入上式。
\(\begin{align*} T(n)&=2^{\log n}T(1)+n(\log n\times\log n-\frac{\log n(\log n-1)}{2}) \\ &=n+n\times \frac{\log^{2}n+1}{2}\\ \end{align*}\)
故,总的时间复杂度为 \(\mathcal{O}( n\log^2 n)\) 。
4.其他
该章节收录个人认为有意思的题目。
4.1
(NOIP2012普及组)如果平面上任取 \(n\) 个整点(横纵坐标都是整数),其中一定存在两个点,它们连线的中点也是整点,那么 \(n\) 至少是几?
分析一下两个点的中点是整点有什么性质, \((x_1,y_1),(x_2,y_2)\) 的中点是 \((\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\) ,要求中点是整点,所以 \((x_1+x_2)\) 和 \((y_1+y_2)\) 均要是偶数。所以从整点坐标的奇偶性来讨论,只有\((奇,偶)(奇,奇)(偶,奇)(偶,偶)\) 四种情况,所以可以发现至少要 \(5\) 个点。
4.2
(NOIP2017提高组)若 \(f(0)=0,f(1)=1,f(n+1)=\frac{f(n)+f(n-1)}{2}\) ,则随着 \(i\) 的增大, \(f(i)\) 接近于?
本题共有四种解法。其中,值得声明的是,该“解法一”并不严谨,故称之为“做题技巧”或许更佳。
解法一:
本题的原题是一道选择题,于是我们可以递推 \(f(i)\) 的值,不难发现 \(f(i)\) 仅接近于选项中的 \(\frac{2}{3}\) ,这题就可以“猜”出来了。
为了避免这种不严谨的做法,我去掉了选项,接下来,让我们来好好看看这题应该怎么做。
解法二:
我们可以将 \(f(i)\) 写成二进制小数,即 \(0,1,0.1,0.11,0.101,0.10101,0.101011,\cdots,0.10101010\cdots\) ,不难发现趋向于 \(0.10101010\cdots\) ,即 \(\frac{2}{3}\) 。
解法三:
这是一个挺常见的trick,用初等的方式解出了本题。
\(\begin{align*} f(n+1)&=\frac{f(n)+f(n-1)}{2} \\ f(n+1)+\frac{1}{2}f(n)&=f(n)+\frac{1}{2}f(n-1)\\ f(n+1)-f(n)&=-\frac{1}{2}[f(n)-f(n-1)]\\ \end{align*}\)
不妨设 \(a_i=f(i)-f(i-1)(i\in \mathbb{N}_{+})\) ,特别地 \(a_1=1\) ,则有 \(a_{i+1}=-\frac{1}{2}a_i\) 。
不难发现 \(\left \{ a_i \right \}(i\in \mathbb{N}_{+})\) 是公比为 \(-\frac{1}{2}\) 的等比数列。
我们易得: \(\begin{align*} \sum_{i=0}^{k}a_i=f(k)-f(0)=f(k) \end{align*}\)
结合等比数列的求和公式,本题就迎刃而解了。
\(\begin{align*} f(n)&=\sum_{i=0}^{n}a_i=[1-(\frac{1}{2})^n]\times \frac{2}{3} \end{align*}\)
当 \(n\to \infty\) 时, \(f(n)=\frac{2}{3}\) 。
解法四:
该解法较高等,有余力的读者可以试着参考解法完成本题。
可利用生成函数待定系数法求通项公式后,再令 \(n\) 趋向于无穷。
我们不难得到该数列的特征方程为: \(x^2=\frac{x+1}{2}\) ,解得 \(x_1=1,x_2=-0.5\) 。
列出如下方程组: \(f(0)=0=c_1\times1^0+c_2\times(-0.5)^0\) 和 \(f(1)=f=c_1\times1^1 +c_2\times (-0.5)^1\) 。
解得 \(c_1=\frac{2}{3},c_2=-\frac{2}{3}\) ,所以 \(f(i)=\frac{2}{3}-\frac{2}{3}(-\frac{1}{2})^i\) ,显然当 \(i\) 趋向于正无穷时, \(f(i)\) 趋向于 \(\frac{2}{3}\) 。
鸣谢
感谢 \(lym,lyx,zps\) 对本文的整理与归纳做出的贡献。
本文有部分内容援引或改编自《信息学奥赛一本通》以及网络。


