Fenwick树状数组

基本思想：

　　树状数组是用来解决在数组元素动态变化的情况下，高效的计算子数组和的一种数据结构，其更新效率和计算和的效率均为O（logn），和普通的sum数组不同的是，虽然sum数组计算子数组和的效率为O（1），但是在面对数组元素动态变化的情况下，其更新效率为O（n）。Fenwick数组的更新方式如下图：

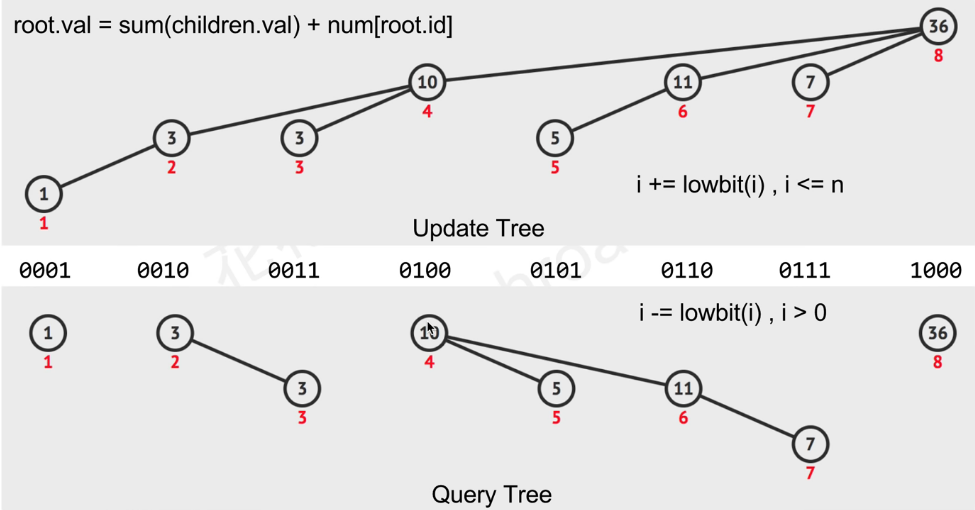
　　首先需要一个辅助函数lowbit，用于计算最低位所在的位置，比如二进制110，那么它返回的是二进制10，这个函数利用补码的特性x&（-x）即可实现。有了这个函数，就可以实现数组的更新与查询。我们需要两个数组vec和tree，vec用于存储原始数据，tree是树状数组。对于更新操作，记录下该位置和原始数据之差diff，然后i += lowbit（i）进行更新。对于i到j之间的子数组之和，计算0到j和0到i两部分的和相减即可，而对于0到i之和，从第i个数开始i -= lowbit（i），并将tree[i]相加即可。代码如下，即Leetcode 307答案

class NumArray {
public:
    NumArray(vector<int> nums) {
        vec = vector<int>(nums.size(),0);
        tree = vector<int>(nums.size()+1);
        for(int i = 0;i != nums.size();++i){
            update(i,nums[i]);
            vec[i] = nums[i];
        }
    }
    
    void update(int i, int val) {
        int diff = val-vec[i];
        vec[i] = val;
        int index = i+1;
        while(index < tree.size()){
            tree[index] += diff;
            index += lowBit(index);
        }
    }
    
    int sumRange(int i, int j) {
        return getSum(j+1)-getSum(i);
    }
private:
    vector<int> tree;
    vector<int> vec;
    int lowBit(int x){
        return x&(-x);
    }
    int getSum(int x){
        int result = 0;
        while(x > 0){
            result += tree[x];
            x -= lowBit(x);
        }
        return result;
    }
};

 　　这是一维树状数组的情况，我们拓展一下思考二维的情况，即Leetcode 308，二维应该怎么处理呢，首先我们肯定需要一个二维数组存储真实值，对于update函数，我们对横坐标和纵坐标累加lowbit(x)，代码如下

class NumMatrix {
public:
    NumMatrix(vector<vector<int>> matrix) {
        if(matrix.size() == 0) return;
        grid = vector<vector<int>>(matrix.size(),vector<int>(matrix[0].size(),0));
        tree = vector<vector<int>>(matrix.size()+1,vector<int>(matrix[0].size()+1,0));
        for(int i = 0;i != matrix.size();++i){
            for(int j = 0;j != matrix[0].size();++j){
                update(i,j,matrix[i][j]);
            }
        }
    }
    
    void update(int row, int col, int val) {
        int diff = val-grid[row][col];
        grid[row][col] = val;
        col += 1;
        row += 1;
        for(int i = row;i < tree.size();i += lowbit(i)){
            for(int j = col;j < tree[i].size();j += lowbit(j)){
                tree[i][j] += diff;
            }
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        return getSum(row2+1,col2+1)-getSum(row1,col2+1)-getSum(row2+1,col1)+getSum(row1,col1);
    }
private:
    int getSum(int row,int col){
        int result = 0;
        for(int i = row;i > 0;i -= lowbit(i)){
            for(int  j = col;j > 0;j -= lowbit(j))
                result += tree[i][j];
        }
        return result;
    }
    int lowbit(int x){
        return x&(-x);
    }
    vector<vector<int>> grid;
    vector<vector<int>> tree;
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * obj.update(row,col,val);
 * int param_2 = obj.sumRegion(row1,col1,row2,col2);
 */

 

参考资料：

 　　https://www.youtube.com/watch?v=WbafSgetDDk&t=748s