【读书笔记】计算机图形学基础（虎书）第7章 - 视角

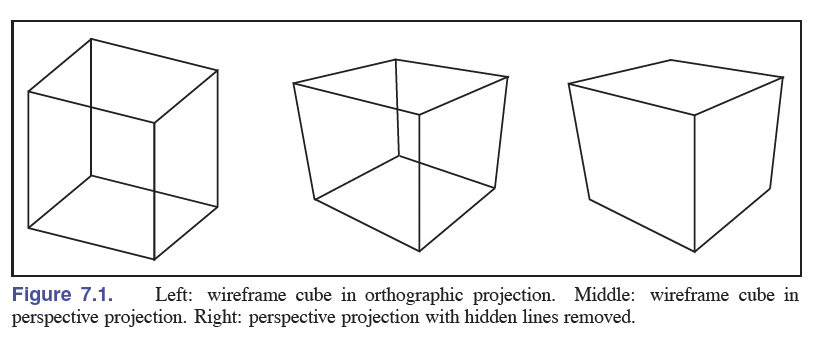
这里翻译基于另一位前辈同一章节的学习笔记。除了第六章提到的旋转等操作以外，一个重要的转换矩阵是将三维物体转换至二维屏幕视图的Viewing Transformation(观察变换)，主要用在object-order rendering（物体为顺序的渲染）上。从直接的转换矩阵来看我们只能将所有点或者线框(wireframe)进行展示，并且不能马上处理如下图第三个的远近遮挡关系。我们需要另一个方法来处理前后关系，其中一个方法是我们可以用一个代表远近的\(z\)值进行渲染优先度的分析，会在之后进行讨论。

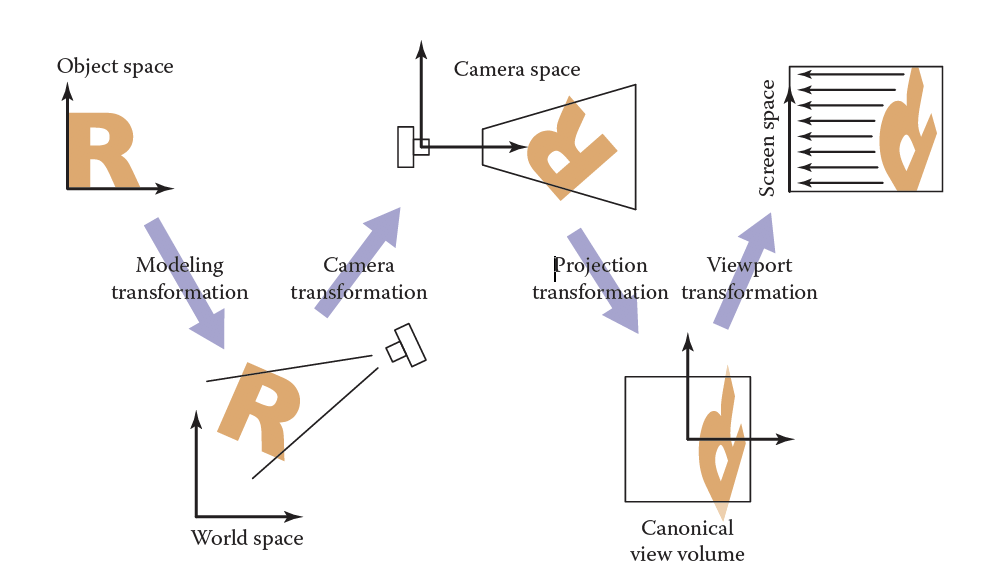
观察变换矩阵的本质是将全局坐标系下\((x,y,z)\)坐标投影到以像素为坐标单位的屏幕上。我们通常将整个变换分为多个步骤进行转换，具体可以见下图，涉及到物体局部坐标系、全局坐标系、相机坐标系、标准空间与屏幕空间。前瞻来讲一下标准空间和屏幕空间的区别，标准空间将整个屏幕视为一个面积为1（或者4，边是[-1,1]）的单位方形，而屏幕空间则由屏幕大小（行列像素个数）来决定。以下小章节按照倒序对整个观察变换进行一一讲解。

1. Viewport Transformation（视口变换）

因为标准空间的定义各有一些不一样，例如本书利用\([-1,1]\)的方形，也有以左上角为\((0,0)\)右下角为\((1,-1)\)的投影，此节主要介绍思想。总的来说，视口变换要将标准空间平面与像素平面一一对应，按照本书的规范标准空间为\([-1,1]\)的方形而屏幕空间的像素位置按照对应方格的中心为准，因此是\([-1,1]\times[-1,1]\)至\([-0.5, n_x-0.5]\times[-0.5,n_y-0.5]\)的空间变换。这里要注意\(n_x-0.5\)里的\(n_x\)是横轴像素的个数而不是像素的最大序号。考虑到标准空间转换至屏幕空间，因为标准空间的单位基对应屏幕空间\((n_x/2,n_y/2)\)，可以直接依次进行倍率转换和位移操作，这里位移需要将屏幕中心移动到屏幕的左下角，故移动\((-0.5+n_x/2,-0.5+n_y/2)\)，总结得到如下转换矩阵。

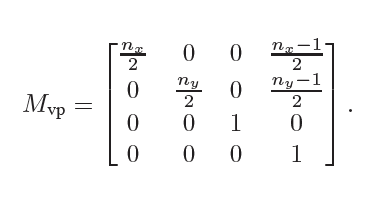
2. Projection Transformation(投影转换)

投影转换将相机空间的三维物体转换至标准空间的二维图片。整体来讲是按照照相机(camera)或者眼睛(eye)构造坐标系，并通过不同的方式将三维物体投影到视觉平面上。

2.1 长方体视野

第一种方法是将视野范围设置为长方体，如下图所示。注意这里因为右手坐标系的原因\(z\)轴正方向靠后，因此摄像机的正方向是沿着\(-z\)方向。因此更大的\(z\)值(更小的负值)代表了更近的位置。

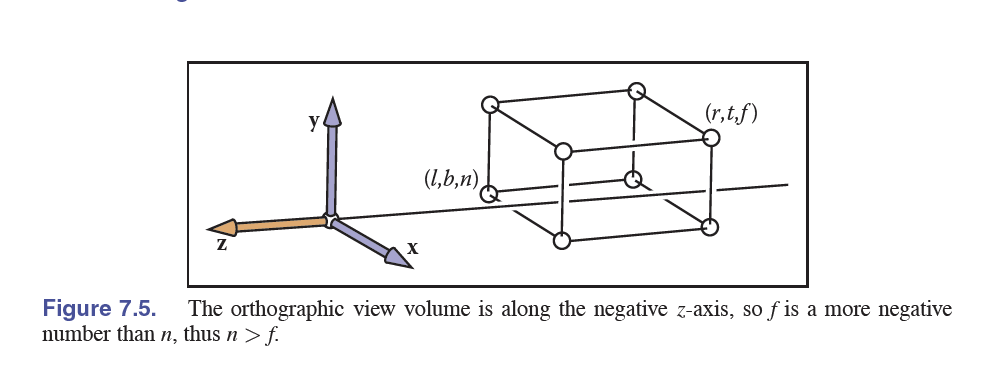
具体转换公式可以见下图，注意这里是将相机空间转换到标准二维空间，第四列考虑的是相机空间原点在标准二维空间下的位置。标准二维空间原点在相机空间下是\((\frac{r+l}{2},\cdots,\cdots)\)，反向距离则为\((-\frac{r+l}{2},\cdots,\cdots)\)。相机空间的\((r-l,t-b,n-f)\)个单位长对应二维标准空间的2个单位长（这里使用的是\([-1,1]\)的正方体，如果使用其他标准则有改变）。因此，第四列的位置为\((\frac{-\frac{r+l}{2}}{\frac{r-l}{2}},\cdots,\cdots)=(-\frac{r+l}{r-l},\cdots,\cdots)\)。前三列是基变换，即一单位的的二维标准空间基是一单位的全局三维坐标系统通过什么变换得来的。如果通过求逆矩阵来思考第四列则会更加直观，立方体的中心点是\((\frac{r+l}{2},\cdots,\cdots)\)，求对应将全局三维空间转换到二维标准空间的逆矩阵第四列为\(\frac{r+l}{2}\cdot\frac{2}{r-l}=\frac{r+l}{r-l}\)，取逆矩阵增加负号得到\(-\frac{r+l}{r-l}\)。

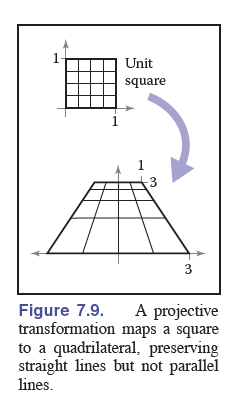
2.2 Projective Transformation（透视转换）

透视转换比起之前的投影转换不仅更符合人体所见的近大远小原则，而且扩展了可见视野的范围（中心长方体外拥有额外空间，减少更近更小的一半，增加更远更大的一半，基于相似三角形原则整体必然增大），具体如下图。

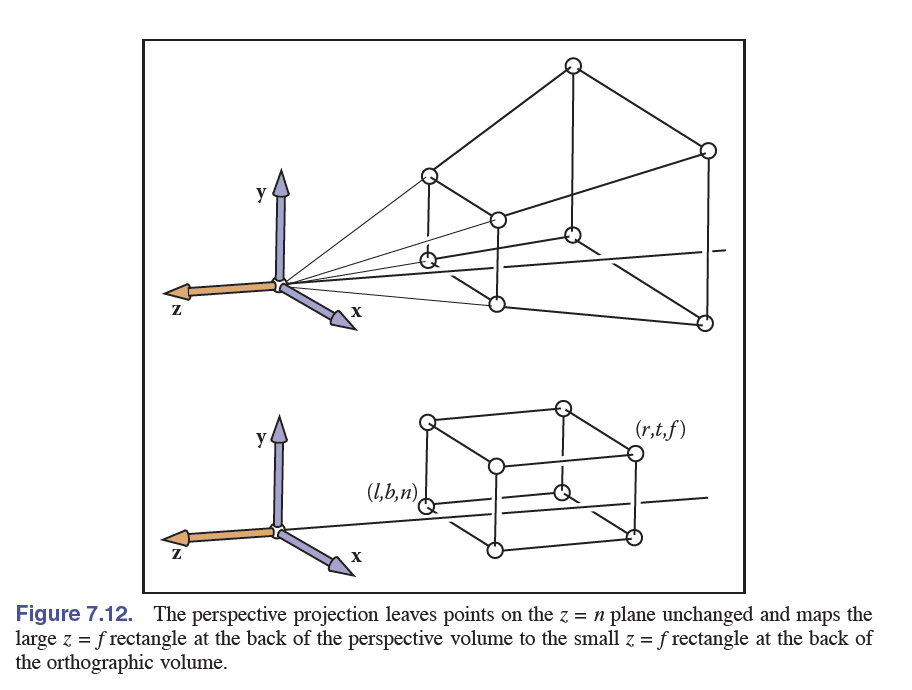
在讲解透视转换时先加入齐次坐标的另一运用。之前提及齐次坐标可以做到平移的操作，但第四行仅使用了\([0,0,0,1]\)。如果将第四行更改到其他值，则转换的范围就进一步拓展到类似于\(x'=\frac{a_1x+b_1y+c_1z+d_1}{ex+fy+gz+h}\)的地步，具体如下。基本上第四行决定了缩放受到\(xyz\)方向值的影响程度。


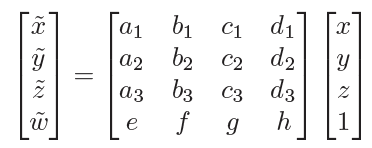
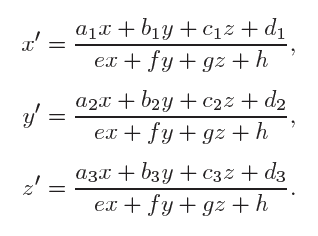
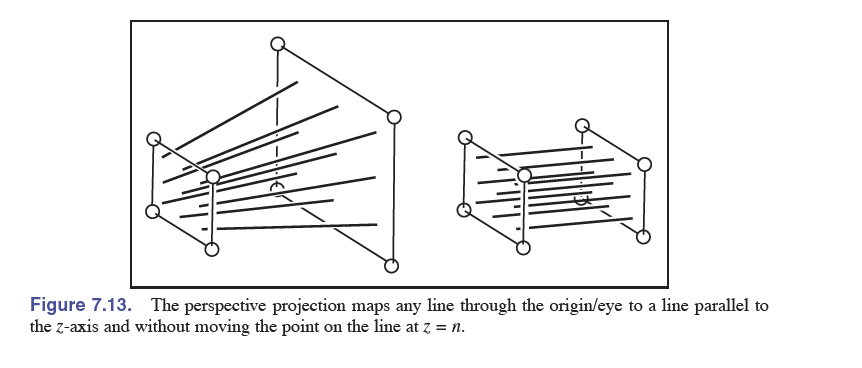
这里需要注意，虽然整个转换矩阵是线性的，但是就三维移动的点来讲转换是非线性的。可以见此图。

在实际计算时，我们假定上为\(y\)，右为\(x\)，后为\(z\)的右手坐标系，那么向前的方向为\(-z\)。假设远近平面分别为负值的\(f,n\)，那么远近平面的距离分别为\(-f,-n\)。本书采取的方法是将透视六面体(Frustrum, 截头体)先转换成长方体视野再转换成二维视觉平面，透视转换还有很多其他的方法。从透视六面体(Frustrum)转换到长方形视野的转换矩阵如下，转换时设置为按照近平面\(n\)的大小创造长方体视野。

公式上，首先通过相似三角形应该得到\(y'=\frac{n}{z}y,x'=\frac{n}{z}x\),因此我们得知一个初始的方法为第一行\([n,0,0,0]\)，第二行\([0,n,0,0]\)，第四行\([0,0,1,0]\)，现在需要考虑第三行。为了让\(z\)值在转换后不变，即\(\frac{ax+by+cz+d}{z}=z\),此方程明显无解，因此\(z\)值一定会有所改变。下方的转换矩阵使\(f,n\)平面上的\(z\)值不变，中间的按不同比率进行变动，改变方法为\(\frac{(n+f)z-fn}{z}\)。


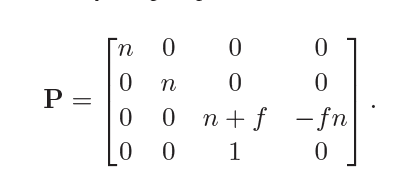
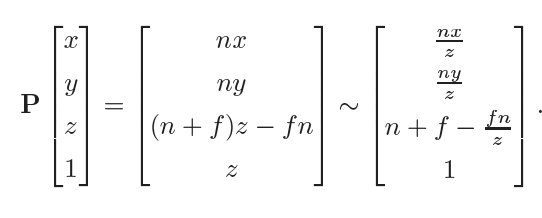
注意其逆矩阵有以下的简单写法，无需额外花时间进行逆矩阵运算。第二个逆矩阵依然成立是因为齐次坐标下\(kP\)与\(P\)的转换效果是一致的，故恒可以乘除一个常数，此处乘了一个\(nf\)。

整个透视转换可以简单的记录为\(M_{orth}P\)，即将透视六面体(Frustrum, 截头体)先转换成长方体视野再转换成二维视觉平面的过程，合并也可以得到以下算式。

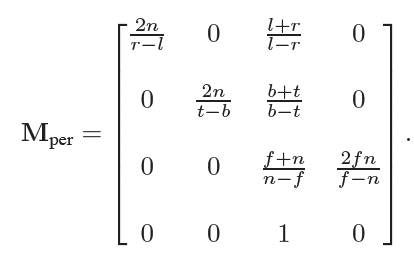
2.3 视野(Field of View)

如果我们假设目光穿过中心，则有\(l=-r,b=-t\)。采取长宽比一致的情况，即\(\frac{n_x}{n_y}=\frac{r}{t}\)。因为\(f\)通常通过可见度来设置，我们的透视转换矩阵里能够调整的仅仅剩下\(n\)。我们往往设置一个垂直视野(vertical field of view)的角度\(\theta\)，即\(tan(\frac{\theta}{2})=\frac{t}{|n|}\)来改变\(n\)的值从而调整整个透视的六面体frustrum。显而易见当\(\theta\)更大，则\(n\)更接近且整个透视frustum会更大，但远处更大的\(f\)面被压缩在同样大小的\(n\)面投影中，导致远处场景的压缩程度更大。

3 摄像机转换

通常摄像机用相机位置的eye position(e)，眼睛所看的方向gaze(g)或者其他(look,forward等)，以及向上的方向view up(t)来表示。注意这里\(t\)并不需要垂直向上，只需要\(tg\)构成一个垂直平分世界的平面即可。按照前文所提及的右手坐标系,注意\(z=-g\),右手的\(x\)可以通过\(z\times v\)得出，垂直向上的\(y\)可以通过\(x\times z\)得出。注意中间要将向量长度转换为\(1\)(normalize)。直接转换得到以下矩阵，注意\((xyz)\)对应\((uvw)\)。因为将全局空间坐标系转换到相机空间坐标系，可以先位移再变基。注意变基说的是一个全局单位\(x\)在\(uvw\)坐标系下的坐标\((x_u,x_v,x_w)\)，坐标为什么是这个可以参考本视频，主要是因为u在x轴的投影\(x_u\)依据单位长向量的对称性等于x向量在u方向上的投影，故\(x_uu+x_vv+x_ww=x\)。另一个更为简单的方法是因为坐标系三者互相垂直，形成正交基，故逆矩阵等于转置矩阵。

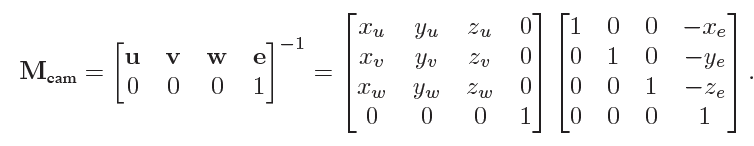
4. 结论
至此，我们完成了从全局坐标系到相机空间到标准空间到屏幕空间的变化，只需要把转换矩阵从右到左依次相乘即可，见下图。