【读书笔记】计算机图形学基础（虎书）第1章 - 介绍
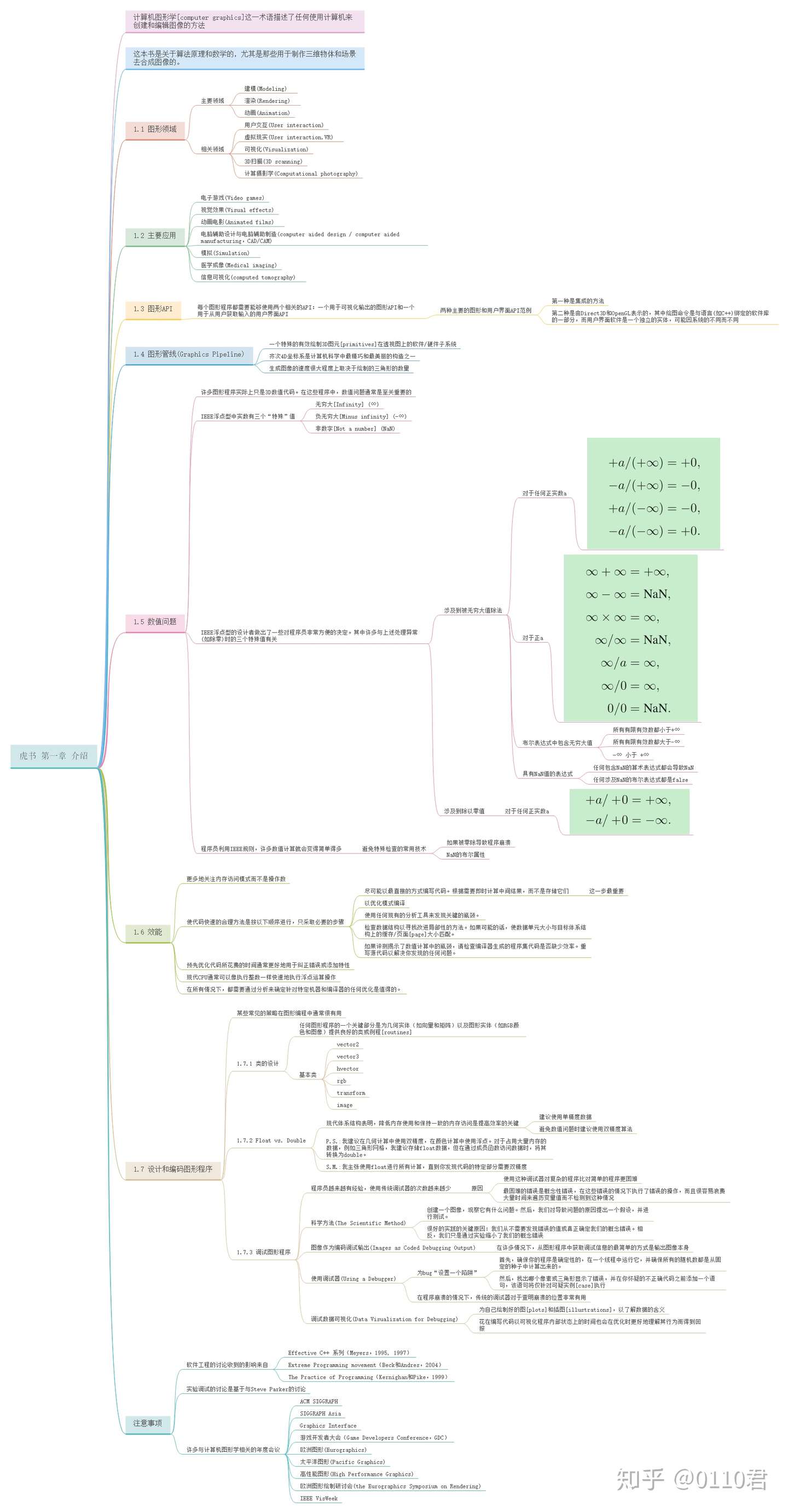
第一章 - 介绍
1. 计算机图形学的主要研究领域
最重要的是以下三个
- 建模（骨），以数学方法，利用点线连接与反射模型等对物理世界物体进行建模，并编写与周围物件的交互方式
- 渲染（皮肉），为3D模型添加光影、材质、环境等
- 动画（动作），利用一连串的图片伪造持续运动的错觉，时间（例如关键帧的处理）为重要的因素。
其他也包括用户交互、虚拟现实（VR）、（各类）可视化、图片处理（PS等修图）、3D扫描、摄影（拍照滤镜）
2. 计算机图形学的主要应用领域
-电子游戏，例如光照，实时渲染，纹路等
-卡通动画，例如3渲2、3D动画等
-电影特效，例如绿幕后期，存在带动电影界改革的现象
-CAD/CAM，Computer Aided Design/Manufacturing，例如工程/建筑建模、3D打印建模以及最近的VR绘画/建模等
-模拟，例如飞行模拟器、赛车模拟器等
-医学成像，各类扫描技术，已经逐渐可以获得带颜色的3D图来寻找病灶
-数据可视化，寻找特殊的绘图方式给较为杂乱的数据归纳总结
3. 图形API
平台介绍
为了更好的跨平台与GPU和其他硬件进行沟通，一些高级抽象的图形学API被发明出来，主要分为以下两种。
- UI与图形结合，例如Java为基础的图形学API，利用各平台通用的package来开发
- 仅编写图形，例如Direct3DD和OpenGL，需要额外设计UI。常见的例如C++后台的OpenGL+设计UI的Qt
后一种API可移植性较低，需要通过其他的方法来处理多平台的问题，例如检测运行环境再使用不同的程序。
回调函数（callback function）
在与前端UI进行交互时，往往使用callback（回调)的方法。(英文解释，中文解释)。具体来讲，区别于常见的修改A函数并在函数内调用B函数，我们选择将B函数放在A函数的参数内（指针引用等方法）。通过这种方法即使A函数被封装好，我们也可以通过修改A函数的参数来实现不同的目的。例如当前端UI的按钮被点击时，触发一个button_Pressed(void (*callback)(void))的函数，我们可以选择不同的callback函数放到button_Pressed()的参数内，例如exit_game()和start_game()，这样同类的两个button可以触发两个不同的事件。
4. 三维模型
在图形学中，最常见的三维模型是以若干个三角形组成、共享顶点、全封闭的三角网格（3D mesh）。具体的数据结构差距较大，个人使用过的是半边结构（half-edge）。
5. 图形管线（Pipeline）
此部分具体见后面的章节，总体来讲，图形管线的设计目的是以分层的方法来增加绘图的效率与可理解性，现在的图形管线主要优化三维三角形与共享顶点的绘制。对于初学者来讲，一种粗略的理解是从内存提取顶点信息->按某种规则处理顶点信息->三角形化顶点（获得边等信息）->光栅化（根据边等信息寻找哪些像素应该被绘制）->决定每个像素应该被怎么画->把像素画到屏幕上）
如果你有一些英语基础并希望在此阶段对图形管线有所了解，请点击此链接
图形管线中每一步都有值得分析的操作，其中最重要的一步即在坐标系中采取4x4的矩阵，前三列代表xyz位置，而最后一列使用齐次坐标（homogenous coordinate)的技巧，主要服务于 3D空间内的坐标变换，这样坐标变换就可以轻松的用连续的矩阵相乘来表示（而不是一些加一些乘）。 又例如在光栅化的时候我们要决定哪一个物体更靠近摄像机并被绘制，在此会运用到一个z-buffer的技巧，即将物体到摄像机的距离算作z向量，记录每一个像素点内最近的z向量与对应的图形，加以绘制，过程比较像图论单元最短路问题中更新距离矩阵。
就绘制效率而言，图形管线的速度基本与需绘制的三角形数量成正比。因此，减少需绘制的三角形就成为了一个优化速度的好方法。当绘制较远距离的场景时，经常会通过降低三角形的数量来优化速度，引申出了多层次细节（level of detail）这个概念。另一个例子是只绘画在摄像机前且未被遮挡的物体，这个技巧叫做面剔除(face-culling)。
6. 数值问题（特指数值在计算机内的表达方式问题）
在图形学内因为操控的大部分都是小数，因此数值的精度十分重要。在计算机发展的早期年代，不同硬件采取不同的数值标准，为可移植性带来巨大的困扰。现在在绝大部分地方通用的IEEE浮点标准为我们免去很多烦恼，但是仍需维持对于浮点数精度问题的认识和注意。一个例子是在之前Z-buffer的例子中，如果Z值极其类似，例如1.00与0.9999999，可能会存在误判导致图形的重叠交错效果，具体图片可见此文章
在IEEE的特殊值中，我们需要注意正无限，负无限，正0，负0与NaN值（undefined）。
除了直觉上正确的大小无限与实数关系外，总结逻辑为
- 无限作为被除数或\(0/0\)时结果为NaN
- 无限相减结果为NaN（无限之间不分大小）
- 含NaN的代数操作结果一定为NaN
- 含NaN的逻辑操作结果一定为NaN
- 除了\(0/0\)以外，被除数为0时结果为无限
- 结果的符号取决于前两个元素的符号，例如 \(+a/(-\infty)=+0\)
需注意对于逻辑运算符转换来讲，正无限被视作TRUE，负无限与NaN被视作FALSE。
7. 代码效率(Efficiency)
因为现代CPU与多核的研发，代码效率分析的重心慢慢从操作的数量（Operation Count，我们常说的时间复杂度）转移到内存访问模式（倾向于空间复杂度，但着重于内存放的位置、调用方法、cache、云空间等）。
本书推荐的方法是
- 以最快的方式把代码写出来
- 以优化模式（optimized mode）去编译代码
- 用分析工具发现瓶颈问题
- 检查数据结构来直接改进，尽量让数据大小与机器cache/page的大小一致，减少分割数据的时间
- 检查编译器代码是否缺乏效率，重写源代码解决问题。
使用第一步的主要目的是为了将预先优化代码的时间用于纠正错误和添加新的特性，并且很多预先优化并没有起到作用，反而使代码变的复杂和难以阅读。与此同时，开发者需要对现存技术有所了解，例如CPU的进化使其处理整数和浮点数差不多快、编译器的一些自我优化等，这样能避免一些无意义的优化。
8 图形程序的设计与编程
常用的类(Class)
通常使用234维向量代表点位置、4x4矩阵代表变换方式、3色RGB（代表像素颜色）和图片的数据格式。另外常用四元数（quarternion）来代表方向（主要理解、代数），此阶段略看即可。
单精度vs双精度浮点（float vs double）
原则上选择一个来用，具体哪一个视开发情况而定。普遍来讲double的精度更大，可保持数值操作更稳定且更贴近于真实数学。float占据空间较小，操作更快。
调试图形程序
- 科学方法
像科学家一样，生成一个图像看有什么问题，提出一个假想或猜测、测试然后修改问题。这种方法需要对底层知识有所了解，有相对丰富的经验去猜测问题可能发生的原因，并不适合新手。好处是可以快速的缩小概念错误的可能范围。 - 利用图像作为调试输出
通过输出图像来进行调试，例如在猜测曲面的法线是不是写错了的时候，可以屏蔽其他图，把法线转换成一条带颜色的单位向量并进行观察来调试，如果全部线垂直往外为正确，否则错误。其他例子包括绘制温感图查看检测人物移动时皮肤变形错误是不是因为骨骼顶点影响系数写错了，如果温感图确实越靠外温度越低，那么才是正确。 - 调试技巧
因为通常会遍历很多点和三角形，我们需要特殊的方法来进行调试。例如如果我们发现（5，5）这个像素点有问题，我们就额外编写代码并跳转至此，而不是连续点击step next至（5，5）。同时打印信息在里面找异常处、如其他程序一样在必要时抛出异常等也是很好的方法。 - 调试的数据可视化
将中间结果放入R、matlab、excel或python之类的数据可视化地点，分析数据的含义，查看是否符合期望。此部分与图像调试输出类似。例如光线追踪器中可视化光线树。(个人对此的感悟并不深，需要以后添加其他例子)
