MNI模板和Talairach 模板的对比

The MNI brain and the Talairach atlas

SPM 96 and later use standard brains from the Montreal Neurological Institute. The MNI defined a new standard brain by using a large series of MRI scans on normal controls. Recall that the Talairach brain is the brain dissected and photographed for the famous Talairach and Tournoux atlas. The atlas has Brodmann's areas labelled, albeit in a rather approximate way. In fact what the authors did was to look at pictures of the Brodmann map and estimate where the same place was on their brain. To quote from the atlas, p 10: "The brain presented here was not subjected to histological studies and the transfer of the cartography of Brodmann usually pictured in two dimensional projections sometimes possesses uncertainties".

The MNI wanted to define a brain that is more representative of the population. They created a new template that was approximately matched to the Talairach brain in a two-stage procedure. First, they took 250 normal MRI scans, and manually defined various landmarks, in order to identify a line very similar to the AC-PC line, and the edges of the brain. Each brain was scaled to match the landmarks to equivalent positions on the Talairach atlas. This resulted in the 250 atlas brain that is very rarely used.

They then took an extra 55 images, and registered them to the 250 atlas using an automatic linear registration method (Collins). They averaged the registered 55 brains with the 250 manually registered brains to create the MNI 305 atlas. The MNI 305 brain is made up of all right handed subjects, 239 M, 66 F, age 23.4 +/- 4.1). See Louis Collins' thesis for a detailed description; the conference paper by Evans et al also describes the process, as does a recent (August 10th 2006) email by Andrew Janke.

The MNI305 was the first MNI template. The current standard MNI template is the ICBM152, which is the average of 152 normal MRI scans that have been matched to the MNI305 using a 9 parameter affine transform. The International Consortium for Brain Mapping adopted this as their standard template; it is the standard template in SPM99 and later. Since then the ICBM has created the ICBM452 template. There are two versions: the air12version is the average of 452 brains after 12 parameter AIR linear transform to the MNI305, whereas the warp5version used AIR for affine and 5 order polynomial non-linear warping - see http://www.loni.ucla.edu/ICBM/Downloads/Downloads_452T1.shtml. ICBM452 is not yet widely used.

In addition, one of the MNI lab members, Colin Holmes, was scanned 27 times, and the scans were coregistered and averaged to create a very high detail MRI dataset of one brain. This average was also matched to the MNI305, to create the image known as "colin27". colin27 is used in the MNI brainweb simulator. SPM96 used colin27 as its standard template. You can download a copy of this image at 1mm resolution from our site; SPM96 and later contains a 2mm resolution copy of the same image, in the canonical directory of the SPM distribution. In SPM96 this is called T1 in later distributions it is called single_subj_T1. Note that the images in the SPM "templates" directories have all been presmoothed to 8mm for use with the normalization routines.

The problem introduced by the MNI standard brains is that the MNI linear transform has not matched the brains completely to the Talairach brain. This is probably because the Talairach atlas brain is a rather odd shape, and as a result, it is difficult to match a standard brain to the atlas brain using an affine transform. As a result the MNI brains are slightly larger (in particular higher, deeper and longer) than the Talairach brain. The differences are larger as you get further from the middle of the brain, towards the outside, and are at maximum in the order of 10mm. In particular, MNI brain is ~5mm taller (from the AC to the top of the brain) and ~5mm longer. The temporal lobes go about 10mm deeper in MNI (see e.g. MNI coordinate X = 32 Y = -4 Z = -50; the lowest slice in the Talairach atlas is at -40). Another example of the mismatch is that at -8 -76 -8 you are firmly in the occipital cortex in the MNI brain, whereas the same coordinates in the Talairach atlas put you in CSF.

The differences are not obvious on axial sections, but are clear on coronal slices. The picture below shows the MNI 152 averate brain section from the SPM distribution, next to the equivalent section of the Talairach atlas. The section is at y = -4; there is a vertical line at 30mm in x, and horizontal lines at z = 0, 73 and -41, the AC top and bottom of the Talairach brain. As the picture shows, the top of the brain is higher in MNI, and the temporal lobes are considerably lower and larger than for the Talairach brain:

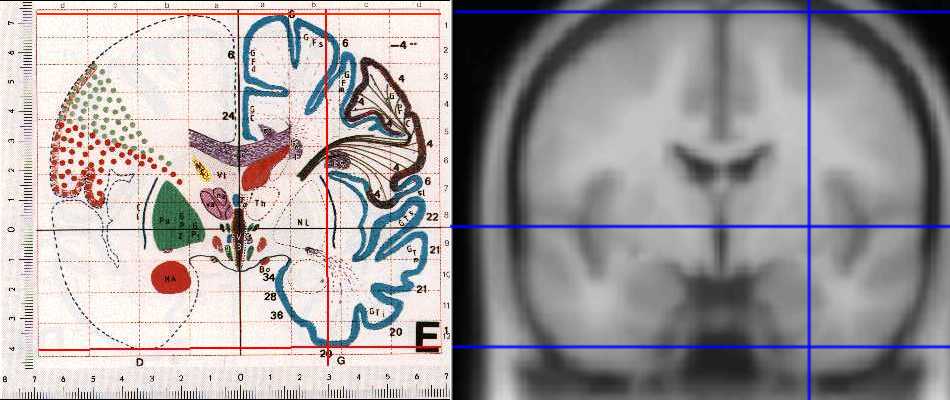
As we discussed above, SPM uses the brains from the MNI for its templates. SPM99 and later uses the MNI average of 152 scans, and SPM96 uses the scan data from the individual brain that has been scanned many times.

This means that the Talairach atlas is not exactly accurate for interpreting coordinates from SPM analyses, if (as is almost always the case) the scans have been spatially normalized (coregistered) to the SPM templates. This can be problem, as, to my knowledge, there is currently no published MNI atlas, defining Brodmann's areas on the MNI brain. In contrast there is widely available, if imprecise, information on Brodmann's areas for the Talairach atlas.

The SPM authors have referred to the coordinates from SPM analyses (matched to the MNI brain) as being 'in Talairach space'. By this they mean that the coordinates are reported in terms of the system that Talairach developed, with coordinate 0,0,0 being at the anterior commissure (AC), and with the anterior / posterior commissural line (AC/PC line) defining the the plane where z = 0. (In fact the AC is not exactly at 0,0,0 in the MNI brain, but about 4mm below - see the 152 T1 average brain in the canonical directory). However, they do not mean by this that the coordinates match the brain in the Talairach atlas, because this is not precisely the case.

 

Converting MNI coordinates to Talairach coordinates

 

So, if you have coordinates for an image already normalized to SPM-MNI space, what are the equivalent cooordinates in Talairach?

There is no definitive answer to this. The problem is that the Talairach brain is a significantly different shape to the MNI brain. In particular the temporal lobes are relatively larger in the MNI brain. Recall that the MNI has already been coregistered to the Talairach brain with linear transforms; the reason that this has not resulted in a very good match is the difference in brain shape.

So, here are two approaches to translating MNI coordinates to Talairach.

 

Approach 1: redo the affine transform

 

This very reasonable approach has been posted to the SPM mailing list in 1998 by Andreas Meyer-Lindenberg, of NIMH. The following is copied from the text of that message, with a small correction (kindly pointed out to me by Darren Gitelman on the SPM mailing list):"I have taken the SPM 95 PET template (which is reasonably "Talairach 88-compatible", as far as I know) and used the spatial normalization algorithm of SPM 96 with an affine transform to map it onto the SPM 96 template (which is "MNI compatible"). If you do this and disregard parameter values for the affine transform that are very small, you come up with the following formulae for translating between the two coordinate systems:

To get from McGill [MNI] -SPM96-coordinates to Talairach 88-SPM 95 coordinates:

X' = 0.88X-0.8

Y' = 0.97Y-3.32

Z' = 0.05Y+0.88Z-0.44"

So, to get a best guess at where your MNI point would be on the Talairach atlas, using the method described above, you can use matlab. Place the following matlab function somewhere in your matlab path (save the following as aff_mni2tal.m):

 

function outpoint = aff_mni2tal(inpoint)
Tfrm = [0.88 0 0 -0.8;0 0.97 0 -3.32; 0 0.05 0.88 -0.44;0 0 0 1];
tmp = Tfrm * [inpoint 1] ';
outpoint = tmp(1:3)';

 

Let us say that you have a point, from the MNI brain, that you want some Talairach equivalent coordinate for. The point might be: X = 10mm, Y = 12mm, Z = 14mm.

With this function on your path, you could type the following at the matlab prompt:

 

aff_mni2tal( [10 12 14] )

 

Which would give the following output (see above):

 

ans =

    8.0000    8.3200   12.4800

 

This gives you the affine method's estimate of the equivalent X, Y and Z coordinates in the Talairach brain.

There are two problems with this approach:

• The first problem is very simple; we have no MRI scan of the brain in the Talairach atlas. The SPM95 brain was smaller than the MNI brain, but it is still not a perfect match for the Talairach atlas.
• The second problem is the same as the problem with the orginal transform done by the MNI: the brains are a different shape. For example, because the temporal lobes are fatter in the MNI brain, the affine transform needs to squeeze these down, by multplying the Z coordinates by a factor of about 0.88. However, this results in the top of the brain being pulled rather too far down, so that it is about 6mm below the highest point on the Talairach atlas.

 

Approach 2: a non-linear transform of MNI to Talairach

 

An alternative is to use some sort of transformation that may differ for different brain areas. One method might be to do an automated non-linear match of the MNI to the Talairach brain. For example, you could apply an SPM or AIR warping algorithm. However, there are two problems here. First, as we stated above, we do not have an MRI image of the brain in the Talairach atlas, which was a post-mortem specimen. Second, the automated non-linear transforms produce quite complex equations relating the two sets of coordinates.An alternative is to apply something like the transform that Talairach and Tournoux designed; here different linear transforms are applied to different brain regions. This is the approach I describe below.

To get a good match for both the temporal lobes and the top of the brain, I used different zooms, in the Z (down/up) direction, for the brain above the level of the AC/PC line, and the brain below. The algorithm was:

• I assumed that the AC was in the correct position in the MNI brain, and therefore that no translations were necessary;
• Assumed that the MNI brain was in the correct orientation in terms of rotation around the Y axis (roll) and the Z axis (yaw);
• Using the SPM99 display tool, I compared the MNI brain to the images in the Talairach atlas;
• Compared to the atlas, the MNI brain seemed tipped backwards, so that the cerebellar / cerebral cortex line in the sagittal view, at the AC, was too low. Similarly, the bottom of the anterior part of the corpus collosum seemed too high. I therefore applied a small (0.05 radian) pitch correction to the MNI brain;
• Matching the top of the MNI brain to the top of the brain in the atlas, required a zoom of 0.92 in Z. Similarly a Y zoom of 0.97 was required as a best compromise in matching the front and back of the MNI brain to the atlas. The left / right match required a 0.99 zoom in X;
• The transform above provided a good match for the brain superior to the AC/PC line, but a poor match below, with the temporal lobes extending further downwards in the MNI brain than in the atlas. I therefore derived a transform for the brain below the AC/PC line, that was the same as the transform above, except with a Z zoom of 0.84;

This algorithm gave me the following transformations:

Above the AC (Z >= 0):

X'= 0.9900X

Y'= 0.9688Y +0.0460Z

Z'= -0.0485Y +0.9189Z

Below the AC (Z < 0):

X'= 0.9900X

Y'= 0.9688Y +0.0420Z

Z'= -0.0485Y +0.8390Z

The matlab function mni2tal.m implements these transforms. It returns estimated Talairach coordinates, from the transformations above, for given points in the MNI brain. To use it, save as mni2tal.m somewhere on your matlab path.

So, taking our example point in the MNI brain, X = 10mm, Y = 12mm, Z = 14mm:

With the mni2tal.m function above on your path, you could type the following at the matlab prompt:

 

mni2tal( [10 12 14] )

 

Which would give the following output (see above):

 

ans =

    9.9000   12.2692   12.2821

 

which is, again, an estimate of the equivalent X, Y and Z coordinates in the Talairach brain.

The inverse function, tal2mni.m, gives MNI coordinates for given Talairach coordinates, using the same algorithm.

We could of course do a more complex transform to attempt to make a closer match between the two brains. The approach above is only intended to be preliminary. It does have the advantage that it is very simple, and therefore the distortions involved are easy to visualise, and unlikely to have dramatic unexpected effects.

Incidentally, if you use the above transform, and you want to cite it, I suggest that you cite this web address. The transform is also mentioned briefly in the following papers: Duncan, J., Seitz, R.J., Kolodny, J., Bor, D., Herzog, H., Ahmed, A., Newell, F.N., Emslie, H. "A neural basis for General Intelligence", Science (21 July 2000), 289 (5478), 457-460; Calder, A.J., Lawrence, A.D. and Young,A.W. "Neuropsychology of Fear and Loathing" Nature Reviews Neuroscience (2001), Vol.2 No.5 352-363

 

Doing better then mni2tal

 

The mni2tal is of course a very crude transform, and it may be possible to do considerably better using an automated approach. Kalina Christoff, RhodriCusack and I (MatthewBrett) used this method for an abstract presented at HBM - see http://www.mrc-cbu.cam.ac.uk/~matthew/abstracts/MNITal/mnital.html

 

Other methods for locating your activation

 

Other methods that you can use to work out where your activation is are;

• Use the SPM 99 and 96 overlay displays to show you the activations on the MNI brain. If you know your anatomy well, or can see the equivalent structures in the Talairach atlas, then you may know where your activation is. Unfortunately, outside the primary sesorimotor cortices, the relation of functional areas to sulcal anatomy can be very variable;
• Use the Talairach atlas, and try by eye to take into account the difference in brain size (given that the differences are relatively small). Obviously this can be inaccurate, and it is very difficult to standardise across labs.

Matthew Brett 5/8/99, updated 14/2/02

References

J. Talairach and P. Tournoux, "Co-planar Stereotaxic Atlas of the Human Brain: 3-Dimensional Proportional System - an Approach to Cerebral Imaging", Thieme Medical Publishers, New York, NY, 1988

J. C. Mazziotta and A. W. Toga and A. Evans and P. Fox and J. Lancaster, "A Probablistic Atlas of the Human Brain: Theory and Rationale for Its Development", NeuroImage 2:89-101, 1995

A. C. Evans and D. L. Collins and B. Milner, "An MRI-based stereotactic atlas from 250 young normal subjects", Journal Soc. Neurosci. Abstr. 18: 408, 1992

A. C. Evans and D. L. Collins and S. R. Mills and E. D. Brown and R. L. Kelly and T. M. Peters, "3D statistical neuroanatomical models from 305 MRI volumes", Proc. IEEE-Nuclear Science Symposium and Medical Imaging Conference, 1813-1817, 1993.