新手学信息检索6：谈谈二值独立模型

介绍一个概率检索模型-二值独立模型。这个模型我自认为比较扯淡，如有大神在可以指点一下。这个模型用了N多个假设。

假设1：词项之间的出现是相互独立的。

这样文档和查询都可以向量化，如下：

当词项t出现在文档或查询中，则x_t或q_t的值为1，否则为0。由于我们假设词项出现是相互独立的，并且向量取值只取0,1两个值，故这个模型就叫做二值独立模型。那么这个模型是如何进行文档检索以及排序的呢，接下来就详细介绍一下。

给定一个查询Q，文档D与Q相关的概率可以用P(R=1|(D,Q))表示，不相关的概率可用P(R=0|(D,Q))表示。

，

。

那么我们自然能想到一个可以用来进行排序的指标：P(R=1|(D,Q))，但是实际中常用下面的式子作为排序的指标：

为了方便计算这个函数，做了几个假设。

那么可以从式子中去掉不影响排序结果，所以式子又变成如下形式：

接下来引入词项的独立性：

 

上面的式子很好理解，既然每个词出现时相互独立的，那么一篇文档出现的概率自然是每个词出现的概率的乘积。

我们观察这个式子发现，如果需要计算这个式子的值必须要计算不在文档内出现的词的一些信息，而不出现在文档中的词的规模是词典的大小，所以计算起来非常耗时，故又提出一个假设来避免对不必要的词进行的计算。

假设3：当t不出现在查询中时，令p_t=u_t。

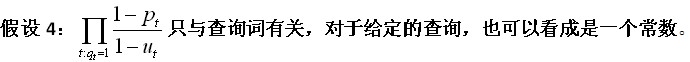
故该项可以略去，不会影响排序效果。并且这个式子中用到了乘法操作，计算过程中很容易产生精度损失，故把其取对数得：

这样我们就只需考虑同时出现在文档和查询中的词进行计算从而提高了效率，并且有效的避免了乘法的精度损失问题。

综上所述，这个模型好处就是推导过程比较直观，缺点就是用了很多假设。但是实际中据说这种模型在某些情况下的效果还不错（我没做过，所以不好说）。

但是反过头来，这个模型到底怎么去使用？有一个困惑的地方在于：我们说它是一个检索模型，但是现在怎么看它都只是一个排序函数而已。并且，无法知道文档与查询的相关性，故p_t 与u_t是不知道的，这又导致了这个模型在这个时候没法计算。既然作为检索模型，那么就必须单独使用就可以得到检索到用户满意的文档，而不能依赖于其它的方法。再仔细观察上面的排序函数的推导过程，我们发现主要难点在于不知道p_t 与u_t。 如果这两个东西知道了，那么后面就自然能得到。说起来比较扯淡，要使用这种模型必须首先自己估计一个p_t 与u_t。 而且估计过程类似于一个迭代的过程。大致过程如下：

（1）初始设置u_t=df_t/N,p_t=0.5

（2）利用初始的估计进行文档的相关性计算，并根据排序函数值进行排序。

（3）默认结果列表中前R个文档是与查询相关，后面N-R个与查询不相关。

（4）根据这R个相关文档和N-R个不相关文档重新计算p_t 与u_t。

其中第4步可以这么计算：

其中p_t=r/R, u_t=(df_t-r)/(N-R)，有时为了避免分母为0，用平滑方法处理得到的这两个值，就这样不断迭代，直到得到用户的满意结果为止。可以看到这种检索方法可能需要很多遍的计算。并且初始值怎么选取还有R怎么选取也很是一个很有争议的问题，这也是这个模型的最大缺点。