堆栈应用(五):离线等价类
1、问题描述
例子:假定 n= 1 4, R= { ( 1 , 11 ), ( 7 , 11 ), ( 2 , 1 2 ), ( 1 2 , 8 ), ( 11 , 1 2 ), ( 3 , 1 3 ), ( 4 , 1 3 ), ( 1 3 , 1 4 ),( 1 4 , 9 ), ( 5 , 1 4 ), ( 6 , 1 0 ) }。我们忽略了所有形如 ( a , a )的关系,因为按照反身属性,这些关系是隐含的。同样也忽略了所有的对称关系。比如 ( 1 , 11) € R,按对称属性应有 ( 11,1) €R。其他被忽略的关系是由传递属性可以得到的属性。例如根据 ( 7 , 11) 和( 11 , 1 2 ),应有(7,12) €R。如果(a , b) €R,则元素a 和b 是等价的。等价类( equivalence class)是指相互等价的元素的最大集合。 “最大”意味着不存在类以外的元素,与类内部的元素等价。
考察例 中的等价关系。由于元素 1 与11, 11 与1 2是等价的,因此,元素 1 , 11 , 1 2是等价的,它们应属于同一个等价类。不过,这三个元素还不能构成一个等价类,因为还有其他的元素与它们等价(如 7)。所以 { 1 , 11 , 1 2 } 不是等价元素的最大集合。集合 { 1 , 2 , 7 , 8 , 11 , 1 2 } 才是一个等价类。关系 R还定义了另外两个等价类: { 3 , 4 , 5 , 9 , 1 3 , 1 4 } 和{ 6 , 1 0 }。
定义:假定有一个具有 n 个元素的集合U= { 1, 2, . . ., n},另有一个具有 r 个关系的集合 R= { (i1, j1) ,(i2 , j2 ), ..., (ir , jr ) } 。关系 R是一个等价关系( equivalence relation),当且仅当如下条件为真时成立:
• 对于所有的 a,有(a, a) €R 时(即关系是反身的)。
• 当且仅当 (b, a) € R时(a, b) €R(即关系是对称的)。
• 若(a, b) €R且(b, c) €R,则有(a, c) € R(即关系是传递的)。
在给出等价关系 R时,我们通常会忽略其中的某些关系,这些关系可以利用等价关系的反身、对称和传递属性来获得。
在离线等价类( o ffline equiralence class)问题中,已知 n 和R,确定所有的等价类。注意每个元素只能属于某一个等价类。
2、解决方法:
可以为n个元素分别建立一个链表,链表其他元素为与当前元素等价的元素。从头扫描元素,对于未输出过的元素,将其先压入一个堆栈,然后扫描对应这个元素的链表,并对这个链表中的元素重复着一过程。直到堆栈为空。
3、代码实现:
堆栈实现见:堆栈的链表方式实现
1 #ifndef OFFLINEEQUIRALENCECLASS_H 2 #define OFFLINEEQUIRALENCECLASS_H 3 4 #include <iostream> 5 #include "Chain.h" 6 #include "LinkedStack.h" 7 using std::cout; 8 using std::cin; 9 using std::endl; 10 11 class offlineEC 12 { 13 public: 14 offlineEC(int n):num(n) 15 { 16 C = new Chain<int>[n + 1]; 17 } 18 19 ~offlineEC(){ 20 if (C!=NULL) 21 { 22 delete[] C; 23 } 24 } 25 26 friend void Offline_Equiralence(); 27 28 private: 29 Chain<int>* C;//存储等价关系的链表 30 int num;//元素个数 31 void findEquiralence();//查找等价类 32 }; 33 34 35 void offlineEC::findEquiralence() 36 { 37 bool *outflag = new bool[num + 1];//标识当前元素是否已经输出到一个等价类了 38 LinkedStack<int> S; 39 ChainIterator<int> CI;//迭代器,遍历链表中的元素 40 41 for (int i = 1; i < num + 1; ++i) 42 { 43 outflag[i] = false; 44 } 45 46 for (int i = 1; i < num + 1; ++i) 47 { 48 if (!outflag[i])//若没有输出过,则是一个新的等价类的开始 49 { 50 cout << "新的等价类:" << i; 51 outflag[i] = true; 52 S.Add(i); 53 while (!S.IsEmpty())//若堆栈不为空,说明还有属于这个等价类的元素 54 { 55 int j; 56 S.Delete(j); 57 int* q = CI.Initialize(C[j]); 58 while (q)//遍历对应的链表,因为一个链表内的元素属于同一个等价类 59 { 60 if (!outflag[*q]) 61 { 62 cout << " " << *q; 63 outflag[*q] = true; 64 S.Add(*q); 65 } 66 q = CI.Next(); 67 } 68 } 69 cout << endl; 70 } 71 } 72 } 73 74 void Offline_Equiralence() 75 { 76 int n, r; 77 cout << "输入元素的个数:" << endl; 78 cin >> n; 79 if (n<2) 80 { 81 std::cerr << "error:元素个数太少" << endl; 82 exit(1); 83 } 84 85 cout << "输入关系对的个数:" << endl; 86 cin >> r; 87 if (r<1) 88 { 89 std::cerr << "error:关系对至少应有1个" << endl; 90 exit(1); 91 } 92 93 offlineEC EC(n); 94 cout << "输入关系对:" << endl; 95 int a, b; 96 for (int i = 0; i < r;++i) 97 { 98 cout << "输入一对关系对:"; 99 cin >> a; 100 cin >> b; 101 while (a>n||b>n||a<=0||b<=0) 102 { 103 std::cerr << "error:元素值输入有误,重新输入" << endl; 104 cout << "输入一对关系对:"; 105 cin >> a; 106 cin >> b; 107 } 108 109 EC.C[a].Insert(0, b); 110 EC.C[b].Insert(0, a); 111 } 112 113 EC.findEquiralence(); 114 } 115 #endif
运行:
1 #include "OfflineEquiralenceClass.h" 2 3 int main() 4 { 5 Offline_Equiralence(); 6 7 system("pause"); 8 return 0; 9 }
运行结果: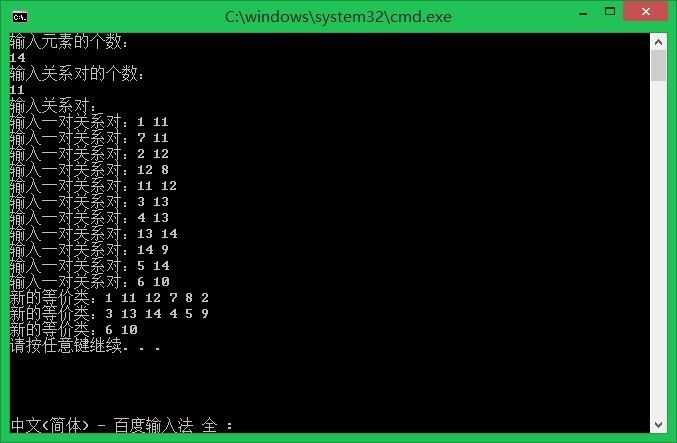
本文来自博客园,作者:CoderInCV,转载请注明原文链接:https://www.cnblogs.com/haoliuhust/p/4262723.html



