数的计算

题目描述

我们要求找出具有下列性质数的个数(包含输入的自然数n):

先输入一个自然数n(n≤1000),然后对此自然数按照如下方法进行处理:

1.不作任何处理;

2.在它的左边加上一个自然数,但该自然数不能超过原数的一半;

3.加上数后,继续按此规则进行处理,直到不能再加自然数为止.

如输入6，由于满足条件的数有6，16，26，126，36，136共六个数，所以输入6结束。

思考流程

思考1

由于此题归类为递归题目，因此第一想法是用递归，递归的代码还是很容易写的，思想也较为简单，与数学归纳法类似。先寻找一个或多个简单结果，找到递归规律，推广到全体结果。

首先先思考几个简单的结论，当自然数n分别为1/2/3时，输出的结果是多少？显而易见，结果应该是1/2/2，其中输入2和3得到的结果一样。

对于之后的数呢？递推规律是什么？我们可以通过画树状图来找到递推规律：

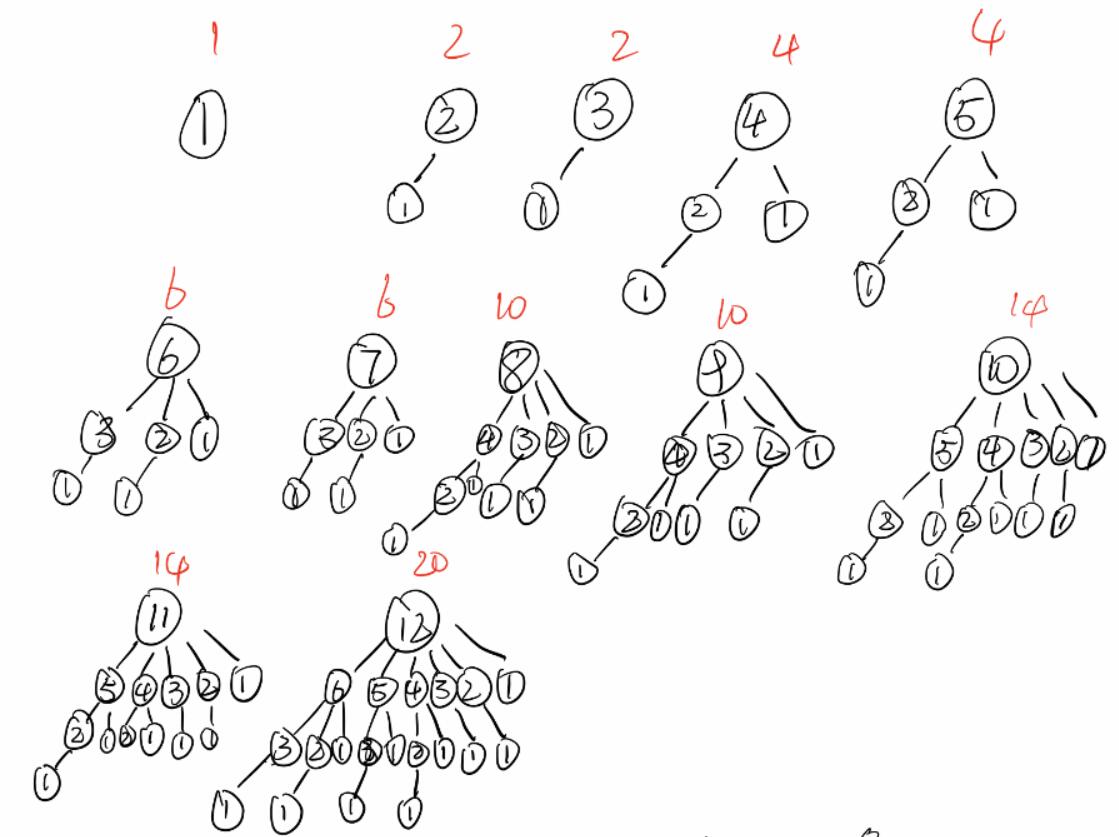
其中用红色字体标出了对每个数、满足条件的数的个数（其实也可以明显看出，我们要求的是树的节点总数）。总结规律如下：
1.\(f(1)=1\)

2.\(f(n)=f(n-1)+f(n/2)\)

由于保管不善，第一版代码已经不复存在了，但是通过递归的一般规律，我们大致能想象，使用递归来做这道题，代码形式较为简单，但其复杂度应是\(O(2^n)\)级别的，这种级别的复杂度实在不能满足题目要求。

那么，如何优化呢？

思考2

显然，递归这条路走不通了，实在是有些遗憾，作为练习题目来说，应该有针对性的练习某项知识点，本题归类为递归，那么递归就该是本题的最优解才对。

虽然遗憾，但是题目还是要继续做下去，我们知道
1.递归之所以复杂度高，是因为重复了许多计算

2.由公式知，计算第n项需要第n-1项和第n/2项，我们可以对已经计算过的答案做存储。

3.此外，观察知，奇数项的答案与它的前一项答案相等。

所以，本次优化，我们将递归改为循环，区分奇偶项，并对每项结果记忆化。综上，我们有如下代码：

#include<stdio.h>
int fun(int n){
	int NodesNum[n]= {1};
	if(n==0||n==1) return NodesNum[0]; 
	else{
		for(int i=1;i<n;i++)
			{
				if((i+1)%2==0) NodesNum[i] = NodesNum[i-1] + NodesNum[(i-1)/2];
				else NodesNum[i] = NodesNum[i-1];
			}
		}
		return NodesNum[n-1];
} 
int main(){
	int x;
	scanf("%d",&x);
	printf("%d",fun(x));
} 

这一版的代码很好的解决了复杂度的问题，在可接受的时间内能给出答案。但这就是最优解了吗？

我想其实我们还能利用k阶线性齐次递推方程来解决这个问题得到通解，无奈本人学艺不精，实在是不会，只盼有高人教教俺。