最小二乘法:从天文学之争到大数据基石
一、引言:从一个测量误差说起
17世纪的欧洲,科学革命正在蓬勃发展。天文学、力学和数学的进步,使得人类第一次有能力对宇宙的运行做出较为精确的预测。然而,即使最先进的观测设备也不可避免地带来测量误差。风速、湿度、光学透镜的不完美、地球大气的扰动,都使得天体观测数据呈现出难以避免的波动。
正是在这样的科学环境中,一种革命性的数学思想逐渐孕育成熟——最小二乘法(Least Squares Method)。它提供了一种数学机制:在存在误差的情况下,如何从一组测量数据中得出“最合理”的参数估计,找到一个对整体最优的解。
从诞生之初,最小二乘法就展现出强大的生命力。它不仅解决了当时急需的天体轨道计算问题,而且迅速传播至物理学、经济学、工程学、统计学等多个学科领域。进入21世纪后,它仍然是数据建模与分析的基石,支撑着机器学习、人工智能等高新技术的发展。
本文将从最小二乘法的历史渊源谈起,系统梳理其理论基础与思想精髓,并结合经典案例与现代发展,全面展示其作为“优化思想原型”的数学魅力。
| 高斯 | 最小二乘法 |
|---|---|
 |
 |
二、历史渊源:从高斯的轨道预言到数学标准的确立
1. 高斯的预言:塞瑞斯星的轨道
1801年,意大利天文学家皮亚齐(Giuseppe Piazzi)发现了一颗新天体,并命名为谷神星(Ceres)。但由于天体移动速度快且太阳遮挡,该星体在后续观测中消失了。
这时,年仅24岁的德国数学天才高斯(Carl Friedrich Gauss)站了出来。他利用皮亚齐所记录的少量观测数据,提出了一种新的估算方法,不仅恢复了谷神星的运动轨道,而且极其精确地预测了它再次出现的位置。
这一壮举震惊了当时的天文学界。1809年,高斯在《天体运动论》(Theoria Motus)中首次公开系统地介绍了其所使用的数学方法——最小二乘法。
2. 勒让德的发表与“发明权”之争
然而,在1805年,法国数学家勒让德(Adrien-Marie Legendre)已在其论文《曲线拟合法》中独立提出最小二乘法,并详细描述了该方法的数值操作步骤。这是最小二乘法最早的公开发表。
高斯坚持认为他早在1795年便已使用该方法,并出示了当年的私人笔记。虽然没有公开发表,但高斯在预测谷神星上的成功极大提升了他的方法声望。
两人之间的“优先权之争”成为学术史上的经典案例。尽管最终未能明确谁为唯一发明者,但这一争议却在客观上加速了最小二乘法的广泛传播。
3. 近代推广:高斯-马尔科夫定理的奠基
到了20世纪,俄罗斯数学家马尔科夫(Andrey Markov)和其学派对最小二乘法的理论基础进行了进一步巩固与推广。尤其是所谓的“高斯-马尔科夫定理”,奠定了最小二乘估计在统计推断中的最优性地位。
三、理论基础:从几何直觉到统计框架
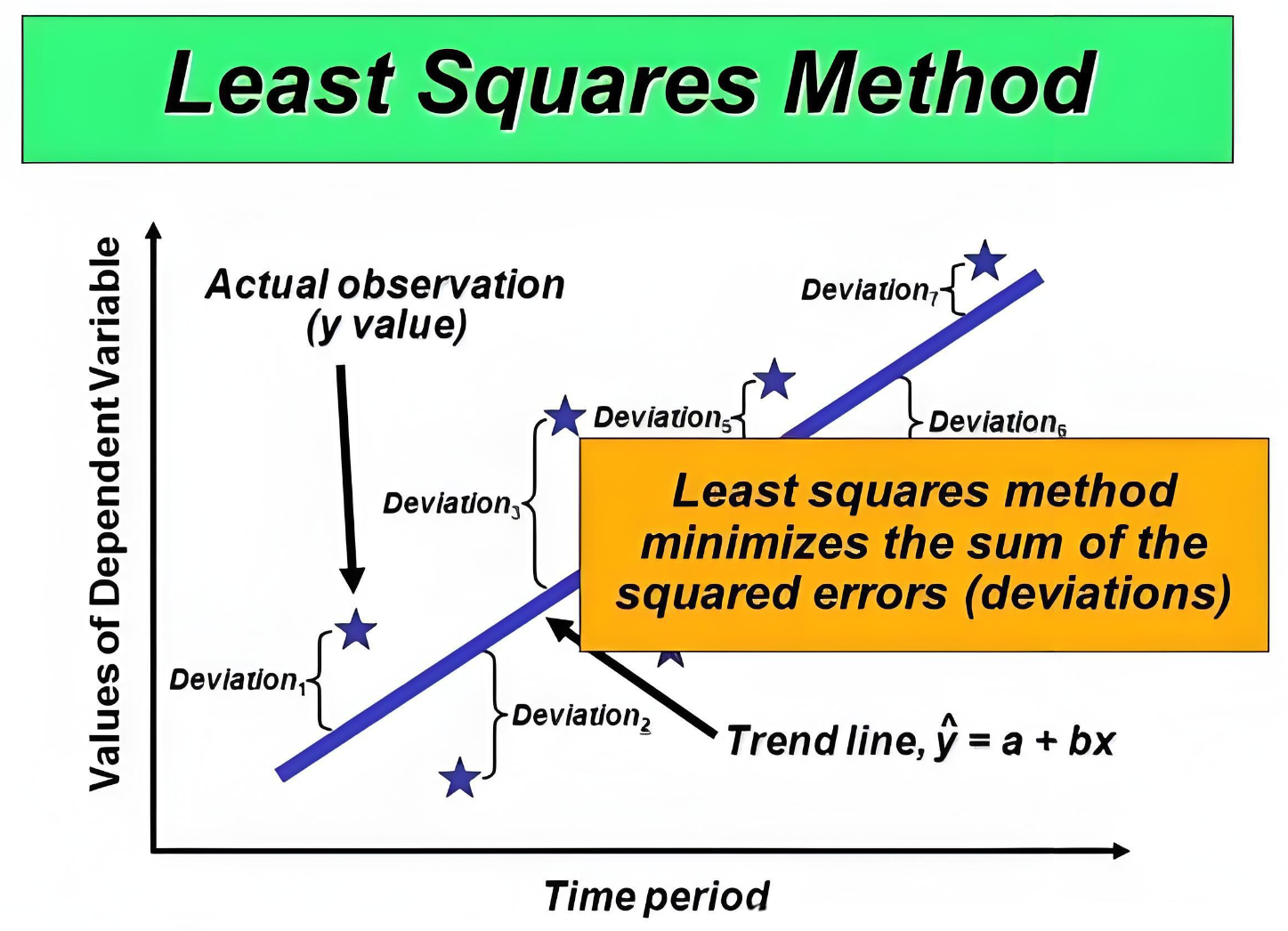
1. 数学公式与直觉解释
最小二乘法的核心思想是:给定一组观测数据点 \((x_1, y_1), (x_2, y_2), ..., (x_n, y_n)\),我们假设观测值满足某种函数模型:
其中,\(\epsilon_i\) 表示误差项,\(\theta\) 为待估参数。
最小二乘法的目标是使误差平方和最小:
2. 几何意义
几何上,这意味着将所有观测点在模型曲线上的正交投影距离最小化。这种“最短距离”的直觉为最小二乘法提供了强大的视觉与空间解释。
3. 统计意义
统计学中,当我们假设误差 \(\epsilon_i \sim N(0, \sigma^2)\) 服从正态分布,最小二乘估计与最大似然估计(MLE)一致,是MLE的一种具体实现形式。
更进一步,最小二乘法也是一般线性模型(GLM)估计的特例,其在误差服从均值为零、方差有限且不相关的情况下,具有“最佳线性无偏估计”(BLUE)的性质。
四、关键人物与学术贡献
1. 高斯(C.F. Gauss):最小误差思想的奠基人
高斯的贡献不仅在于应用最小二乘法预测天体轨道,更重要的是他从概率论角度出发,分析最小二乘估计的性质,奠定了统计推断与误差理论之间的深层联系。他也首次将正态分布引入误差建模中。
2. 勒让德(A.M. Legendre):最小二乘法的首位发表者
勒让德在1805年明确提出用平方和最小化作为拟合准则,为最小二乘法的推广打下了应用基础。尽管其未从概率角度分析误差,但其方法论价值不可忽视。
3. 马尔科夫(A.A. Markov):线性估计理论的缔造者
马尔科夫的研究则深入到了线性无偏估计的理论深处。他构建出“高斯-马尔科夫定理”,指出:在特定条件下,最小二乘估计是线性估计中方差最小的那一个。
这一结果,不仅提升了最小二乘法在统计学中的理论地位,也推动了线性模型体系的建立。
五、最小二乘法的统计地位
1. 回归分析的基石
不论是一元线性回归,还是复杂的多元线性回归、广义线性模型,最小二乘法几乎都构成了建模的核心。
即使在惩罚回归(如Ridge、Lasso)中,也往往以最小二乘为损失函数的基础。
2. 方差分析(ANOVA)
在实验设计与方差分析中,我们通过最小二乘法拟合因变量与因子的关系,并通过拆解总变异来判断因子的显著性。
3. 时间序列分析
在时间序列建模中,如ARMA模型、回归型模型等,最小二乘法仍是重要的估计方法之一。
4. 数值计算中的核心地位
求解正规方程组:\(X^TX\beta = X^Ty\),已经成为统计建模的标准步骤。伴随矩阵理论的发展,这一求解方法极大提升了算法的普适性与数值稳定性。
六、经典案例剖析
1. 身高体重拟合
假设收集100名成年人身高(cm)与体重(kg)的数据,拟合模型:
用最小二乘法估计参数 \(a, b\),即可预测新样本的体重值。
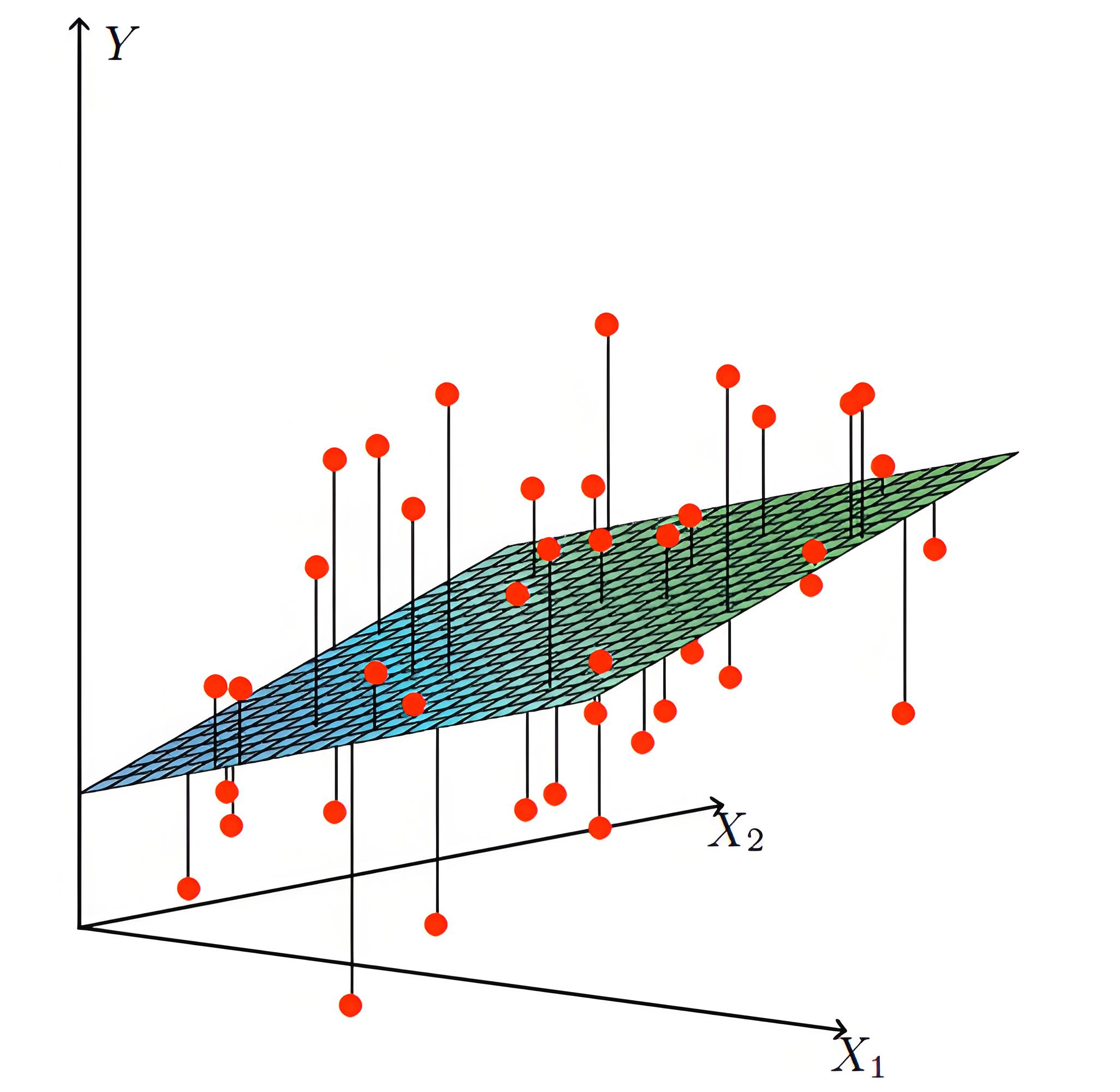
2. 房价预测模型(多元回归)
使用面积、房龄、交通便利度等多种变量作为解释变量,预测房价。
通过求解正规方程组,得到最优参数估计 \(\hat{\beta}\)。
3. 非线性拟合:药物浓度
在药代动力学中,药物浓度随时间呈指数下降:
通过对数线性化变换:\(\log y = \log A - kt\),再使用最小二乘法拟合参数。
七、现代拓展:正则化与机器学习中的最小二乘法
1. 岭回归(Ridge Regression)
为了解决多重共线性带来的不稳定问题,引入惩罚项:
岭回归可有效提高模型的稳健性与泛化能力。
2. Lasso回归:自动变量选择
Lasso通过L1惩罚 \(\lambda\sum |\beta_j|\),实现稀疏解,有助于变量选择,是高维数据建模中的利器。
3. 最小二乘支持向量机(LSSVM)
在机器学习中,LSSVM以平方损失函数替代传统的间隔损失,简化了求解过程,同时保留了支持向量机的非线性映射能力。
八、思想影响:最优化思想的原型
最小二乘法不仅是一种处理数据误差的数学方法,更是一种深刻的数学思想。其核心思想在于,在面对无法避免的测量误差时,通过最小化误差的平方和,从而找到一个能够有效逼近真实关系的最优解。这种最优解并不是直接去除误差,而是通过数学优化,找到一个在所有可能的解中,能最小化整体误差的解。
这一思想不仅奠定了现代统计学和数据科学的基础,也影响了许多后续优化方法的发展。例如,极大似然估计(MLE)就是在最小二乘法思想的基础上扩展而来。在MLE中,我们通过最大化似然函数,从数据中提取参数估计,而这种最大化过程本质上与最小化误差平方和相类似,都是通过最优化来逼近数据的真实分布。
贝叶斯推断进一步发展了最小二乘法的思想,特别是在处理不确定性和先验信息时。在贝叶斯框架下,最小化后验风险成为优化的核心,通过最大化后验分布或最小化损失函数,得到了最优的后验估计。这里的思想和最小二乘法相似:在已有信息的基础上,寻找最可能的解。
EM算法(期望最大化算法)也是在最优化的框架下发展起来的,特别是用于含有隐变量的模型。它通过在期望步骤中计算当前估计下的期望值,然后在最大化步骤中优化参数,反复迭代,逐步接近最优解。这种思想也与最小二乘法中反复调整参数直到误差最小化的过程相类似。
在数值计算方面,梯度下降算法通过沿着梯度方向不断调整参数,达到逐步最小化损失函数的目的,最终逼近最优解。梯度下降本质上就是最小化损失函数的一个数值化过程,广泛应用于机器学习和优化问题中。
在深度学习中,损失函数的设计与优化是训练神经网络的核心部分。通过最小化损失函数,神经网络能够通过大量的训练数据找到最优的模型参数。这一过程的核心与最小二乘法中的优化思想不谋而合:通过反向传播和梯度下降,不断修正模型参数,最终逼近一个能够最小化误差的解。
最小二乘法不仅是一种数值算法,它更代表了一种优化思维的崭新方式。它的提出开创了现代统计学的先河,并对后续所有统计与优化方法的发展产生了深远影响。极大似然估计、贝叶斯推断、EM算法、梯度下降法等后续方法,均是在最小二乘法思想的基础上进行扩展与深化的。通过最小化误差平方和,最小二乘法为我们提供了一个最优解的标准,这一标准至今仍然是数据科学、机器学习与优化问题中不可或缺的核心理念。可以说,最小二乘法不仅仅是一个数学工具,更是现代数据分析与科学计算的基石。
九、参考文献与资料推荐
- Gauss, C. F. (1809). Theoria Motus Corporum Coelestium in Sectionibus Conicis Solem Ambientium.
- Legendre, A. M. (1805). Nouvelles m\u00e9thodes pour la d\u00e9termination des orbites des com\u00e8tes.
- Rao, C. R. (1973). Linear Statistical Inference and Its Applications.
- Stigler, S. M. (1986). The History of Statistics: The Measurement of Uncertainty before 1900.
- Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning.
- Seber, G. A. F., & Lee, A. J. (2012). Linear Regression Analysis.
- Weisberg, S. (2005). Applied Linear Regression.
- Montgomery, D. C., Peck, E. A., & Vining, G. G. (2012). Introduction to Linear Regression Analysis.
本文旨在通过系统性的梳理,帮助读者理解最小二乘法的历史、理论、应用及其背后深远的数学思想。其不仅是一种拟合技巧,更是一段横跨三个世纪、连接经典与现代的数据科学之旅。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号