线性规划的对偶问题及理论
线性规划对偶理论的提出源于1940年代美国数学家冯·诺依曼的工作，他首次引入了对偶的概念。1947年，乔治·丹茨格（George Dantzig）进一步完善了线性规划及其对偶理论，并提出了著名的单纯形法。对偶理论的基础在于每一个线性规划问题（原问题）都可以关联一个对偶问题，这两个问题的最优解之间存在紧密的联系。对偶理论广泛用于经济学、运筹学和工程学。例如，在资源分配问题中，对偶变量代表资源的影子价格或边际效益，这帮助决策者做出更有效的资源配置决策。在网络优化、生产计划和金融投资等领域，对偶理论为优化问题提供了有力的分析工具，促进了复杂问题的求解。对偶理论的应用不仅限于优化问题，它还在博弈论、约束满足问题等方面有着广泛的应用。
| 对偶的矩阵关联 | 对偶转换关系表 |
|---|---|
 |
 |
一、线性规划的对偶问题
对偶问题可以看作是资源外包的数学表达，它提供了一种有效的方法来优化资源的使用。通过对偶问题，原问题中的资源约束可以被视为外包给一个虚拟的市场，从而找到最佳的资源分配策略。这种方法尤其适用于资源有限、需要最大化效率的情况。
1.1 对偶问题引例
王老板有一个家具厂。王老板生产桌子和椅子两种产品，桌子的单价是50元，生产一张桌子需要4个木工工时，2个油漆工工时，椅子的单价为30元，生产一把椅子需要3个木工工时，1个油漆工工时，王老板总计有120个木工工时和50个油漆工工时。两个家具老板的对话如下：
李老板：Hi，王老板，听说近来家具生意好呀，也帮帮兄弟我哦！唉！我想租您的木工和油漆工一用。咋样？价格嘛...好说，肯定不会让您兄弟吃亏。
王老板：价格嘛...好商量，好商量，只是......
李老板内心独白：王老板做家具赚了大钱，可惜我老李有高科技产品，却苦于没有足够的木工和油漆工咋办？只有租咯。
王老板内心独白：家具生意还真赚钱，但是现在的手机生意这么好，不如干脆把我的木工和油漆工租给他，又能收租金又可做生意。
此时，王老板考虑两个问题：第一个自己用木工和油漆工最多能赚多少钱（最大化生产收益），第二个把木工和油漆工出租出去不能低于自己赚的钱（不吃亏原则），并且出租的价格要尽可能低，使得李老板可以接受（[竞争性原则]）。
家具生产模型（原问题，Primal）
资源出租模型（对偶问题，Dual）
王老板按照资源出租模型（对偶规划问题），求解就可以获得其出租木工、油漆工资源的价格，这样既能保证不吃亏（出租资源的租金收入并不低于自己生产时的销售收入），又是的出租价格对李老板有极大的吸引力（李老板所付出的总租金W最少）。本质上，是一种“共赢”。
1.2 线性规划的对偶问题
| 最大变最小 | 最小变最大 |
|---|---|
 |
 |
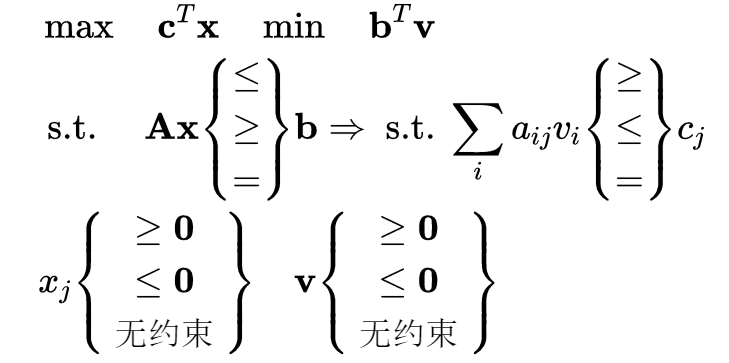对于一个线性规划问题，可以将其表示为如下形式：
其中\(C\)和\(X\)分别表示目标函数的系数和决策变量，\(A\)和\(b\)分别表示约束条件的系数和右侧常数。
对应的对偶问题可以表示为：
其中，\(Y\)表示对偶变量。
1.3例题
原问题：
对偶问题：
1.4例题
原问题线性规划 LP:
对偶问题线性规划 DP:
二、对偶性质
2.1 对偶问题的对偶是原问题
证明：
-
首先写出
- 原问题：\[ \max z = CX \\ \left\{ \begin{array}{ll} AX \leq b \\ X \geq 0 \end{array} \right. \tag{1} \]
- 对偶问题：\[ \min w = b^TX \\ \left\{ \begin{array}{ll} A^TY \geq C^T \\ Y \geq 0 \end{array} \right. \tag{2} \]
- 原问题：
-
把对偶问题转为对称形式：
- min → max：目标函数取相反数。
- 约束条件 ≥ → ≤：约束条件取相反数。\[ \max z = -b^TY \\ \left\{ \begin{array}{ll} (-A^T)Y \leq -C^T \\ Y \geq 0 \end{array} \right. \tag{2'} \]
-
然后，再转对偶问题：
- min → max，≤ → ≥，资源限制 / 收益 位置互换。\[ \min z = -(C^T)^TX \\ \left\{ \begin{array}{ll} (-A^T)^TX \geq (-b^T)^T \\ X \geq 0 \end{array} \right. \tag{1'} \]
- min → max，≤ → ≥，资源限制 / 收益 位置互换。
-
目标函数、约束条件取相反数后，可以发现，对偶的对偶是原问题。
2.2 弱对偶性：生产总收益 ≤ 出租资源的收益
- 若\(X\)是原问题可行解，\(Y\)是对偶问题可行解，则恒有\(CX \leq b^TY\)。
证明：
- 已知限制条件：\(AX \leq b\)，\(A^TY \geq C^T\)。
- 把\(AX \leq b\) 带入要证明的\(CX \leq Y^Tb\) 里，发现\(b^TY = Y^Tb \geq Y^TAX = (A^TY)^TX \geq CX\)，得证。
可以得到一些推论：
- 如果原问题有无界解（生产收益可以无穷大），则对偶问题无可行解（人家收益无穷大，干嘛用有限的钱把资源卖给你）。
- 同样，对偶问题无界解\(\Longrightarrow\) 原问题无可行解。
- 还有一种表述是，原问题有解 对偶问题无界，则原问题有无界解。
- 但是反之不亦然，即，原问题无解推不出对偶问题无界解，对偶问题可能无解 / 无界解。
2.3 强对偶性：最大生产收益 = 最小买资源付出
强对偶定理表明，在线性规划问题中，如果原问题和对偶问题都存在可行解，那么它们的最优目标函数值相等。我们将通过单纯形法的推导，详细证明这一结论。
- 单纯形法与基变量
在单纯形法中，我们选择基变量和非基变量来表示系统的解：
基变量的选择：我们选择\(A\) 的一个满秩子矩阵\(B\)，称为基矩阵。对应的解记为\(X_B\)，其余变量称为非基变量，记为\(X_N\)。
基解的表示：令\(X_N = 0\)，解方程\(A X = b\) 得到\(X_B\)：
其中\(B^{-1}\) 是基矩阵\(B\) 的逆矩阵。
目标函数值：
在基解下，原问题的目标函数值为：
其中$C_B $ 是与基变量对应的目标系数向量。
- 对偶问题的可行解
对偶变量的表示：在对偶问题中，对偶变量$Y $ 可以看作是约束条件的影子价格，表示资源的机会成本。在单纯形法中，我们可以通过基矩阵$B $ 和目标系数$C_B $ 来确定\(Y\)：
需要证明\(Y = (B^{-1})^T C_B^T\) 是对偶问题的一个可行解。这意味着它满足对偶问题的约束：
代入$Y $ 的表达式，有：
由于\(A^T = [B^T, N^T]\)，其中$N $ 是非基列组成的矩阵，分别考虑基变量和非基变量的情况：
- 对于基变量\(j\)，\(A_j\) 是基矩阵\(B\) 的列，有：\[B^T (B^{-1})^T C_B^T = C_B \]因此，显然满足不等式。
- 对于非基变量$j $，约束条件表示为：\[N^T (B^{-1})^T C_B^T \geq C_N \]这是单纯形法中的检验数条件，保证检验数非负，即：\[C_B B^{-1} A_j - C_j \geq 0 \]该条件是保证在每一步迭代中，选择进入基的变量时，目标函数值不会下降的关键。因此，我们可以证明\(Y = (B^{-1})^T C_B^T\) 是对偶问题的一个可行解。
- 从可行解到最优解
由于对偶问题的目标函数值为：\[b^T Y = b^T (B^{-1})^T C_B^T = C_B B^{-1} b \]
这正是原问题的最优目标函数值。因此，我们可以得出结论：如果原问题的基解\(X_B\) 对应的\(Y\) 是可行的，并且\(CX = b^TY\)，那么\(Y\) 也是对偶问题的最优解。
通过单纯形法的推导，我们证明了原问题和对偶问题的最优解的目标函数值相等，具体为\(C_B B^{-1} b = b^T (B^{-1})^T C_B^T\)。这证明了强对偶定理的正确性。原问题的最优解提供了对偶问题的可行解，反之亦然，从而表明线性规划的解在经济学解释和数学理论上都具有对称性。
2.4 互补松弛性：双最优解时，约束条件能否严格取等
- （双最优解情况下）原问题中某一约束条件对应的【对偶变量】≠ 0\(\Longrightarrow\) 该约束条件取严格等式；
- 若约束条件取严格不等式，则其对应的对偶变量一定 = 0。
证明： - 双最优解时，有\(CX = b^TY\)，写成\(CX = Y^Tb\) 的形式，然后有\(Y^Tb = Y^TAX = CX\)，所以有\(Y^T(AX - b) = 0,X^T(A^TY - C^T) = 0\)。
-\(Y^T(AX - b) = 0\)（内积 = 0）说明：① \(AX-b\)松弛变量）每一个元素 与 ② \(Y\)（对偶变量）每一个元素，总有一个 = 0，得证。 - 同理，\(X^T(A^TY - C^T) = 0\) 说明，对偶问题约束条件的 ① 松弛变量 与 ② 在原问题对应的决策变量，总有一个 = 0。（合理，因为对偶的对偶是原问题）。
例：线性规划问题
上述线性规划的最优解是\(X_0=(6,2,0)^T\)，求其对偶问题最优解。
应用松弛互补定理，其对偶问题
给对偶问题的约束方程添加剩余变量：
原问题\(P\)线性规划最优解是\(X^0 = \begin{pmatrix} 6 \quad 2 \quad 0 \end{pmatrix}\)，对偶问题的剩余变量是\(Y_s=\begin{pmatrix} y_3 \quad y_4 \quad y_5 \end{pmatrix}\)。
在互补松弛定理中\(Y_s^0 X^0=0\)，将上述\(X^0\)和\(Y_s\)代入上述式子得到：
已知\(y_3, y_4 \geq 0\)，上述\(6y_3 + 2y_4 = 0\)，因此\(y_3 = 0, y_4 = 0\)；将$ y_3 = 0, y_4 = 0$代入到约束方程
中，得：
得到\(\begin{cases} y_1 + 2y_2 = 3 \\ 2y_1 + 2y_2 = 4 \end{cases}\)，解上述方程，得
上述求出的值就是最优解，即$ Y^0 = \begin{pmatrix} 1 \ 1 \end{pmatrix}$。
2.5 影子价格：对偶问题的最优解 = 资源的边际价格
- 在双最优解的情况下，有原问题的目标函数\(z = CX = Y^Tb\)，其中\(b\)是资源限制。
- 对\(z\)求\(b\)的偏导数，得\(\frac{\partial z}{\partial b} = Y\)，这说明，\(Y\)的各个元素代表了 相应资源每增加一个单位 所能带来的生产收益，也就是边际价格。
影子价格的性质： - 根据互补松弛性，如果生产问题第\(j\)个 ≤ 约束条件取＜而非 =，即第\(j\)种资源没有充分利用，可以推出对偶变量\(i\)= 0，资源\(j\)的影子价格 / 边际价格 = 0。这是合理的，对于没有充分利用的资源，我们并不想花钱买更多。
- 反之，资源\(j\)充分利用\(\Rightarrow\) 资源\(j\)的对偶变量（影子价格）> 0，此时，资源\(j\)只是恰好耗尽而已，而非稀缺。这种情况叫做“退化的最优解”，直观理解，就是在线性规划的图解法中，目标函数的线与约束条件的线重合了。
2.6 检验数：自主收益-外包收益=差额成本(Reduce cost)
影子价格表示一个约束的资源单位变化对目标函数最优值的影响。它与对偶变量紧密相关，在线性规划的最优解中，影子价格等于对偶变量的值，即\(y=C_BB^{-1}\)。
检验数（Reduced Cost）表示在当前解中引入一个非基变量对目标函数的影响。检验数的公式为：
其中，\(A_j^T\)是矩阵\(A\)的第\(j\)列；\(y\)是对偶变量的最优解。
从线性规划原形生产计划问题可知，\(c_j\)是生产该产品的所得的单位利润，\(A_j^Ty\)是生产该产品所耗用资源的价值，或者是将这些资源打包出售所获得的收益，所以是\(c_j\)的机会成本，即以外包方式所获取的利润。
当检验数为负时，说明机会成本\(A_j^Ty\)更高，因此此时出让资源更为有利，不应该自主生产，即引入该变量会降低目标收益。
检验数的绝对值即为差额成本，它表示从当前解状态出发，引入一个单位的非基变量所导致的目标函数值的变化。差额成本解释了引入新的非基变量（或资源）时，对目标函数的改进程度，即选择哪个变量进入基可以带来最大的目标函数改进。
总结
对偶问题不仅是一个重要的数学概念，更是理解和解决现实问题的有力工具。通过引入对偶问题，可以从不同的角度审视原问题，深入理解其结构特征。这种视角转变有助于揭示原问题潜在的规律和最优策略。原问题和对偶问题之间的对称和互补关系使得在一个问题的求解过程中，能够同时获得关于另一个问题的有价值信息。这不仅提高了求解效率，还提供了更全面的理解。由于这种独特的性质，对偶问题在网络优化、金融投资以及诸多科学与工程问题中也展现出了重要的理论价值和实际应用潜力。
