非线性规划——库恩塔克KTT条件（五）

库恩塔克条件(Kuhn-Tucker conditions)是非线性规划领域里最重要的理论成果之一，是确定某点为极值点的必要条件。如果所讨论的规划是凸规划，那么库恩-塔克条件也是充分条件。本文不对数学公式进行详细推导，而是从直观上对KT条件进行理解。

一、带有不等式约束的模型

\[ \min f(X) \\ \text { s.t. } \quad g_i(X) \leq 0, \quad i=1, \ldots, m \Rightarrow \mathbf{m} \text { 个不等式约束 } \\ h_j(X)=0, \quad j=1, \ldots, n \Rightarrow \mathbf{n} \text { 个等式约束 }\]

!!!注意：这里模型不等式约束是小于等于，与清华运筹学标准型相差一个符号，这是为了和软件处理相匹配。

二、库恩塔克条件

KTT条件(Karush–Kuhn–Tucker conditions)是最优化（特别是非线性规划）领域最重要的成果之一，是判断某点是极值点的必要条件。虽然该理论的数学公式看似复杂，但其实它的数学思想极其简单。
对应地，定义的拉格朗日函数为：

\[L\left(X,\left\{\lambda_i\right\},\left\{\mu_j\right\}\right)=f(X)+\sum_{i=1}^m \lambda_i g_i(X)+\sum_{j=1}^n \mu_j h_j(Y) \]

其中，\({λ_i}\)指的是一系列的λ（有\(m\)个），同理{\(μ_j\)}也是。

该最优化问题的KTT条件为：

\[ \nabla f\left(X^*\right)+\sum_{i=1}^m \lambda_i \nabla g_i\left(X^*\right)+\sum_{j=1}^n \mu_j \nabla h_j(X)=0 \quad (1) \\ \lambda_i g_i\left(X^*\right)=0, \quad i=1, \ldots, m \quad (2)\\ h_j\left(X^*\right)=0,\quad j=1, \ldots, n \quad (3)\\ \lambda_i \geq 0, \quad i=1, \ldots, m \quad (4)\\ g_i\left(X^*\right) \leq 0, \quad i=1, \ldots, m \quad (5) \]

解题思路与之前叙述类似，就是用几个等式计算最优值，用不等式验证这些值，不满足则排除。即，利用式(1)(2)(3)求最优\(X^*\)和\(λ_i\)，然后通过式(4)和(5)验证这些解是否可行，“可行”指的是这些解是否能让(4)和(5)的不等号成立，不成立则排除。注意，\(μ_j\)是可以取任意值的，不受限制，因为它们是等式约束的乘子，不是不等式约束的乘子。

2.1 仅有一个不等式约束的情形

$ minf(X) $	$ maxf(X)$
$ g(X) \leq 0 $	$ g(X) \geq 0 $

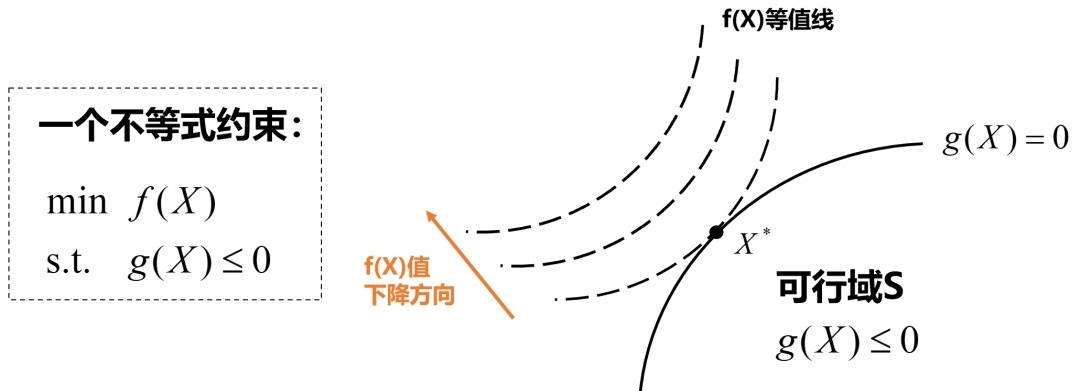
上图画出了3条\(f(X)\)函数的等值线(图中虚线)，由上述分析和上图可知，在最优解\(X^*\)处，\(f(X^*)\)和\(g(X^*)\)的梯度方向共线且方向相反。向量共线且方向相反在数学上的写法就是：

\[-\nabla f\left(X^*\right)=\lambda \nabla g\left(X^*\right) \Rightarrow \nabla f\left(X^*\right)+\lambda \nabla g\left(X^*\right)=0 \]

对于最大化问题，\(f(X^*)\)与\(g(X^*)\)的梯度方向相同，有：

\[\nabla f\left(X^*\right)=\lambda \nabla g\left(X^*\right) \Rightarrow \nabla f\left(X^*\right)-\lambda \nabla g\left(X^*\right)=0\\ \nabla f\left(X^*\right)+\lambda \nabla g\left(X^*\right)=0 \text {, 且 } \lambda<0 \]

2.2 多个约束的情形

假设有起作用约束\(g_1(X)\)和起作用约束\(g_2(X)\)共同影响目标函数\(f(X)\)的梯度，又是怎么样的图形呢？

\(f\)函数的负梯度可以表示成\(g_1\)函数和\(g_2\)函数梯度的线性组合。则有如下公式：

\[\begin{aligned} & -\nabla f\left(X^*\right)=\lambda_1 \nabla g_1\left(X^*\right)+\lambda_2 \nabla g_2\left(X^*\right) \\ & \nabla f\left(X^*\right)+\lambda_1 \nabla g_1\left(X^*\right)+\lambda_2 \nabla g_2\left(X^*\right)=0 \\ \end{aligned} \]

三、实例

例1：验证点 \(\left(\frac{1+\sqrt{17}}{2}, \frac{1-\sqrt{17}}{2}\right)^T\) 与 \((0,-3)^T\) 是否是规划问题

\[\begin{array}{ll} \min & f(x)=x_1^2+x_2 \\ \text { s.t. } & x_1^2+x_2^2 \leq 9 \\ & -x_1-x_2+1 \geq 0 \end{array} \]

的 K-T 点。对 K-T 点写出相应的 Lagrange 乘子。
解:将规划问题标准化

\[\begin{array}{ll} & \min f(x)=x_1^2+x_2 \\ \text { s.t. } & g_1(X)=x_1^2+x_2^2-9 \leq 0 \\ & g_2(X)=x_1+x_2-1 \leq 0 \end{array} \]

\[\nabla f(X)=\left(\begin{array}{l} 2 x_1 \\ 1 \end{array}\right), \quad \nabla g_1(X)=\left(\begin{array}{l} 2 x_1 \\ 2 x_2 \end{array}\right), \quad \nabla g_2(X)=\left(\begin{array}{l} 1 \\ 1 \end{array}\right) \]

\(\text { 记 } X^{(1)}=\left(\begin{array}{c} \frac{1+\sqrt{17}}{2} \\ \frac{1-\sqrt{17}}{2} \end{array}\right) \text {, } \quad X^{(2)}=\left(\begin{array}{l}0 \\ -3\end{array}\right)\)
(1)下面验证正则点:

\[\nabla g_1\left(X^{(1)}\right)=\left(\begin{array}{c} 1+\sqrt{17} \\ 1-\sqrt{17} \end{array}\right), \quad \nabla g_2\left(X^{(1)}\right)=\left(\begin{array}{l} 1 \\ 1 \end{array}\right) \]

显然 \(\nabla g_1\left(X^{(1)}\right)\) 与 \(\nabla g_2\left(X^{(1)}\right)\) 线性无关, 于是 \(\left(\frac{1+\sqrt{17}}{2}, \frac{1-\sqrt{17}}{2}\right)^T\) 为正则点。

\[\nabla g_1\left(X^{(2)}\right)=\left(\begin{array}{l} 0 \\ -6 \end{array}\right), \quad \nabla g_2\left(X^{(2)}\right)=\left(\begin{array}{l} 1 \\ 1 \end{array}\right) \]

同样 \(\nabla g_1\left(X^{(2)}\right)\) 与 \(\nabla g_2\left(X^{(2)}\right)\) 线性无关, 于是 \((0,-3)^T\) 也是正则点。
(2)下面验证是否满足 Kuhn-Tucker 条件:

\[\nabla f\left(X^{(1)}\right)+\sum_{j=1}^2 \gamma_j \nabla g_j\left(X^{(1)}\right)=\left(\begin{array}{l} 1+\sqrt{17} \\ 1 \end{array}\right)+\gamma_1\left(\begin{array}{l} 1+\sqrt{17} \\ 1-\sqrt{17} \end{array}\right)+\gamma_2\left(\begin{array}{l} 1 \\ 1 \end{array}\right)=\left(\begin{array}{l} 0 \\ 0 \end{array}\right) \]

得 \(\gamma_1=-\frac{1}{2}<0, \gamma_2=-\frac{1+\sqrt{17}}{2}<0\), 故 \(\left(\frac{1+\sqrt{17}}{2}, \frac{1-\sqrt{17}}{2}\right)^T\) 不满足 Kuhn-Tucker 条 件。

\[\nabla f\left(X^{(2)}\right)+\sum_{j=1}^2 \gamma_j \nabla g_j\left(X^{(2)}\right)=\left(\begin{array}{l} 0 \\ 1 \end{array}\right)+\gamma_1\left(\begin{array}{l} 0 \\ -6 \end{array}\right)+\gamma_2\left(\begin{array}{l} 1 \\ 1 \end{array}\right)=\left(\begin{array}{l} 0 \\ 0 \end{array}\right) \]

得 \(\gamma_1=\frac{1}{6}>0, \gamma_2=0\), 故 \((0,-3)^T\) 满足 Kuhn-Tucker 条件。

例2：考虑非线性规划问题:

\[\begin{aligned} & \min f\left(x_1, x_2\right)=\left(x_1-1\right)^2+\left(x_2-2\right)^2 \\ & \text { s.t. }\left\{\begin{array}{c} -x_1+x_2=1 \\ x_1+x_2 \leq 2 \\ x_1, x_2 \geq 0 \end{array}\right. \end{aligned} \]

利用Kuhn-Tucker条件求其全局最优解。
解: 构造 Lagrange 函数如下:

\[L(x, \lambda)=\left(x_1-1\right)^2+\left(x_2-2\right)^2+\lambda_1\left(-x_1+x_2-1\right)+\lambda_2\left(x_1+x_2-2\right) \]

根据 Kuhn-Tucker 条件，存在 \(x^*=\left(x_1^*, x_2^*\right)^T\) 和 \(\lambda_1^* \in R, \lambda_2^* \geq 0\)，使得
(1)

\[\begin{aligned} & -x_1^*+x_2^*=1 \\ & x_1^*+x_2^* \leq 2 \end{aligned} \]

(2) $$ \lambda_2^* (x_1^* + x_2^*-2)=0 $$

(3)

\[\begin{aligned} \frac{\partial L}{\partial x_1}=2\left(x_1^* -1\right)-\lambda_1^* + \lambda_2^*=0 \\ \frac{\partial L}{\partial x_2}=2(x_2^* - 2) + \lambda_1^* + \lambda_2^* =0 \end{aligned} \]

设 \(x_1+x_2=2\)，根据条件(1)，我们可求出 \(x_1^*=\frac{1}{2}, x_2^*=\frac{3}{2}\)，将它们代入(3)，有:

\[\begin{aligned} & 2\left(\frac{1}{2}-1\right)-\lambda_1^*+\lambda_2^*=0 \\ & 2\left(\frac{3}{2}-2\right)+\lambda_1^*+\lambda_2^*=0 \end{aligned} \]

由此可得 \(\lambda_1^*=0,\lambda_2^*=1\), 由于点 \(x^*=\left(\frac{1}{2}, \frac{3}{2}\right)\) 满足条件 (1) - (3), 它是 Kuhn -Tucker 点。容易验证, 目标函数 \(f(x)\) 是凸函数, 两个约束函数也都是凸函数，知点 \(x^*=\left(\frac{1}{2}, \frac{3}{2}\right)\) 是全局最优解, \(\bar{f}=\frac{1}{2}\) 是全局最小值。

例3：想建造一个体积至少为64立方英寸的盒子。我们想尽量减少所使用的材料的总量。我们可以将最优化问题表述为：

\[\begin{alignat}{2} \min_{x, y, z}\quad 2xy+2yz+2xz \quad \\ s.t. \quad xyz \geq 64 \qquad \quad \\ x > 0, y > 0, z > 0 \end{alignat} \]

主条件：

\[L(x, y, z, \lambda) = 2xy+2yz+2xz + \lambda (64-xyz) \\ \nabla_xL(x, y, z, \lambda) = (2y+2z- \lambda yz, 2x+2z-\lambda xz, 2y+2x-\lambda xy) = 0 \]

互补条件：

\[\lambda (64 - xyz) = 0 \]

解1： \(λ = 0\)。那么有\(x = y = z = 0\)，该点并不满足原问题可行性
解2： \(λ > 0\)和\(xyz = 64\)。根据第一个等式，就有

\[\lambda = 2(\frac{1}{x} + \frac{1}{y}) = 2(\frac{1}{x} + \frac{1}{z})= 2(\frac{1}{z} + \frac{1}{y}) \]

因此，\(x = y = z = 4\)是KKT条件的唯一解。

例4：考虑下述问题

\[\begin{array}{ll} \min & x_1^2+x_2^2 \\ \text { s.t. } & x_1+x_2=1 \\ & x_2 \leq \alpha \end{array} \]

其中 \(\left(x_1, x_2\right) \in \mathbb{R}^2, \alpha\) 为实数。写出Lagrange函数

\[L\left(x_1, x_2, \lambda, \mu\right)=x_1^2+x_2^2+\lambda\left(1-x_1-x_2\right)+\mu\left(x_2-\alpha\right) \]

KTT 方程组如下:

\[\begin{aligned} \frac{\partial L}{\partial x_i} & =0, \quad i=1,2, \\ x_1+x_2 & =1 \\ x_2-\alpha & \leq 0 \\ \mu & \geq 0 \\ \mu\left(x_2-\alpha\right) & =0 . \end{aligned} \]

求偏导可得 \(\frac{\partial L}{\partial x_1}=2 x_1-\lambda=0\) 且 \(\frac{\partial L}{\partial x_2}=2 x_2-\lambda+\mu=0\) ，分别解出 \(x_1=\frac{\lambda}{2}\) 且 \(x_2=\frac{\lambda}{2}-\frac{\mu}{2}\) 。代入约束等式 \(x_1+x_2=\lambda-\frac{\mu}{2}=1\) 或 \(\lambda=\frac{\mu}{2}+1\) 。合并上面结果，

\[x_1=\frac{\mu}{4}+\frac{1}{2}, \quad x_2=-\frac{\mu}{4}+\frac{1}{2} \]

最后再加入约束不等式 \(-\frac{\mu}{4}+\frac{1}{2} \leq \alpha\) 或 \(\mu \geq 2-4 \alpha\) 。底下分开三种情况讨论。
(1) \(\alpha>\frac{1}{2}\) : 不难验证 \(\mu=0>2-4 \alpha\) 满足所有的KKT条件，约束不等式是无效的， \(x_1^{\star}=x_2^{\star}=\frac{1}{2}\) 是内部解，目标函数的极小值是 \(\frac{1}{2}\) 。
(2) \(\alpha=\frac{1}{2}:\) 如同 \(1 ， \mu=0=2-4 \alpha\) 满足所有的KKT条件， \(x_1^{\star}=x_2^{\star}=\frac{1}{2}\) 是边界解，因为 \(x_2^{\star}=\alpha\) 。
(3) \(\alpha<\frac{1}{2}\) : 这时约束不等式是有效的， \(\mu=2-4 \alpha>0\) ，则 \(x_1^{\star}=1-\alpha\) 且 \(x_2^{\star}=\alpha\) ，目标函数的极小值是 \((1-\alpha)^2+\alpha^2\) 。

例5：求解下面问题

库恩-塔克条件通常用于解决具有约束条件的优化问题，特别是当问题不能简单地通过拉格朗日乘数法解决时。

\[\begin{align*} \text{min } & f(x) = -(x - 4)^2 \\ \text{subject to } & g_1(x) = x - 1 \geq 0 \\ & g_2(x) = 6 - x \geq 0 \end{align*} \]

我们注意到目标函数是一个二次函数，且二次项系数为负，这意味着它是一个下开口的抛物线，因此我们实际上是在寻找该抛物线的最低点。

• 构造拉格朗日函数 $$(L(x, \lambda_1, \lambda_2) = -(x - 4)^2 + \lambda_1 (x - 1) + \lambda_2 (6 - x)$$

• 求偏导数 并令它们等于零来找到\(x\)的值：

  \[\frac{\partial L}{\partial x} = -2(x - 4) + \lambda_1 - \lambda_2 = 0 \]

• 约束条件：

  \[g_1(x) = x - 1 \geq 0 \Rightarrow x \geq 1\\ g_2(x) = 6 - x \geq 0 \Rightarrow x \leq 6\]

• 应用库恩-塔克条件：

  \[\lambda_1 \geq 0 \quad \lambda_2 \geq 0\\ \lambda_1 (x - 1) = 0 \quad \lambda_2 (6 - x) = 0\]

• 解方程组：
  从 \(\lambda_1 (x - 1) = 0\) 和 \(\lambda_2 (6 - x) = 0\) 我们可以看出，如果 \(x = 1\)，则 \(\lambda_1 = 0\)；如果 \(x = 6\)，则 \(\lambda_2 = 0\)。

• 检查边界条件：
  在 \(x = 1\) 时，\(g_1(x) = 0\) 且 \(g_2(x) = 5 > 0\)，满足 \(g_1(x) \geq 0\) 和 \(g_2(x) \geq 0\)；在\(x = 6\) 时，\(g_2(x) = 0\) 且 \(g_1(x) = 5 > 0\)，满足约束条件。

• 确定最优解：
  在\(x = 1\) 时，\(f(x) = -(1 - 4)^2 = -9\)；在\(x = 6\) 时，\(f(x) = -(6 - 4)^2 = -4\)。

由于我们的目标是最小化 \(f(x)\)，因此 \(x =1\) 时的-9是一个比\(x = 6\) 时的-4更优的解。所以最优解是\(x = 1\)，此时\(\lambda_2 = 0\)，\(\lambda_1\)可以是任何非负数，并且目标函数的最小值为\(f(x) = -9\)。

KKT条件是判断某点是极值点的必要条件，不是充分条件。换句话说，最优解一定满足KKT条件，但KKT条件的解不一定是最优解。对于凸规划，KKT条件就是充要条件了，只要满足KKT条件，则一定是极值点，且得到的一定还是全局最优解。

参考文献

1. KKT条件，原来如此简单 (上) | 理论部分
2. KKT条件：不等式约束（五）
3. Karush-Kuhn-Tucker (KKT)条件