决策论——朴素贝叶斯的两个判断准则（四）
在所有的机器学习分类算法中，朴素贝叶斯和其他绝大多数的分类算法都不同。对于大多数的分类算法，比如决策树，KNN，逻辑回归，支持向量机等，他们都是判别方法，也就是直接学习出特征输出\(Y\)和特征\(X\)之间的关系，要么是决策函数\(Y=f(X)\)，要么是条件分布\(P(Y|X)\)。但是朴素贝叶斯却是生成方法，也就是直接找出特征输出\(Y\)和特征\(X\)的联合分布\(P(X,Y)\)，然后用\(P(Y|X)=P(X,Y)/P(X)\)得出。朴素贝叶斯很直观，计算量也不大，在很多领域有广泛的应用。
一、贝叶斯模型描述
贝叶斯学派很古老，但是从诞生到一百年前一直不是主流，主流是频率学派。频率学派的权威皮尔逊和费歇尔都对贝叶斯学派不屑一顾，但是贝叶斯学派硬是凭借在现代特定领域的出色应用表现为自己赢得了半壁江山。贝叶斯学派的思想可以概括为先验概率+数据=后验概率。也就是说我们在实际问题中需要得到的后验概率，可以通过先验概率和数据一起综合得到。数据大家好理解，被频率学派攻击的是先验概率，一般来说先验概率就是我们对于数据所在领域的历史经验，但是这个经验常常难以量化或者模型化，于是贝叶斯学派大胆的假设先验分布的模型，比如正态分布，\(\beta\)分布等。这个假设一般没有特定的依据，因此一直被频率学派认为很荒谬。虽然难以从严密的数学逻辑里推出贝叶斯学派的逻辑，但是在很多实际应用中，贝叶斯理论很好用，比如垃圾邮件分类，文本分类。为便于理解，借用生物细胞的简单二分法，引入本部分的阐述。
设$\omega_1 $代表正常细胞， \(\omega_2\)代表异常细胞(癌细胞)。
$$ P(X)=\sum_{j=1}^{c} P(X|\omega_j)P(\omega_j) \quad c表示总类别数$$
先验概率：预先已知的或者可以估计的模式识别系统位于某种类型的概率。 \(P(\omega_1),P(\omega_2)\)称为先验概率，根据统计资料估计得到，
$$P(\omega_1)+P(\omega_2)=1 \quad P(\omega_1)>P(\omega_2)$$
类条件概率：系统位于某种类型条件下模式样本\(x\)出现的概率。\(P(x|\omega_1),P(x|\omega_2)\)称为类条件概率，根据训练样本统计分析得到。
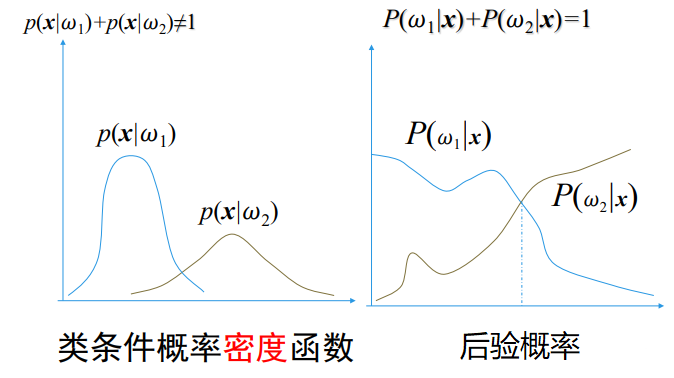
后验概率：系统在某个具体的模式样本 \(x\)条件下位于某种类型的概率，可根据贝叶斯公式计算，用作分类判决的依据。\(P(\omega_1|x),P(\omega_2|x)\) 称为后验概率，
联合概率：\(P(X,\omega_i)\)
贝叶斯决策：在类条件概率密度和先验概率已知的情况下，通过贝叶斯公式比较样本属于两类的后验概率，为使总体错误率最小，将类别决策为后验概率大的一类。
二、最小错误率贝叶斯决策
贝叶斯判别规则是把某特征向量\(X\)落入某类集群的条件概率当成分类判别函数（概率判别函数），\(X\)落入某集群的条件概率最大的类为\(X\)的类别，这种判决规则就是贝叶斯判别规则。贝叶斯判别规则是以错分概率或风险最小为准则的判别规则。
模式特征 \(X\)： \(d\)维特征向量 $X = [ x_1 , x_2 , . . . , x_d ]^T $
分类错误的概率 \(P(e|x)\)：是模式特征\(X\) 的函数
平均错误率\(P(e)\)：是随机函数 \(P(e|x)\)的期望
$$P(e)=\int P(e|x)P(x)dx$$
最小错误率：
若 \(P(\omega_k|x)=\max_{i=1,2}P(\omega_i|x)\)，则$x\in \omega_k $
以两分类问题（癌细胞与正常细胞）为例。
假设根据某种分类规则，模式（特征）空间被分成两个部分（以 \(H\)为分界面）其中\(R_1\)中的样本被分为第一类，\(R_2\)中的样本被分为第二类。
已知先验概率\(P(\omega_1),P(\omega_2)\)，根据数据得到类条件概率\(P(x|\omega_1),P(x|\omega_2)\)。 利用贝叶斯公式得到后验概率\(P(\omega_1|x),P(\omega_2|x)\)
当 \(P(\omega_1|x)=P(\omega_2|x)\) 时的分界线称为决策边界或分类线。
计算错误率：
第一类样本分类错误率：\(\int_{R_2} P(x|\omega_1)P(\omega_1)dx\)
第二类样本分类错误率：\(\int_{R_1} P(x|\omega_2)P(\omega_2)dx\)
平均分类出错率：
当\(R_1\)中的样本满足\(P(\omega_2|x)<P(\omega_1|x)\)时，\(P(e)\)取得最小值。即当$ P(\omega_2|x)=P(\omega_1|x)$时，错误率最小。
等价判定公式
朴素贝叶斯决策规则
则\(X \in \omega_i\)类。
根据贝叶斯公式，将后验概率转化为先验概率来表示
上面公式分母与\(i\)无关，也就与分类无关，故分类规则又可表示为
对两分类问题，若$$P(X|\omega_1)P(\omega_1)>P(X|\omega_2)P(\omega_2)，则X\in \omega_1$$
还可改写为，若
统计学称\(\frac{P(X|\omega_1)}{P(X|\omega_2)}\)为似然比；\(\frac{P(\omega_2)}{P(\omega_1)}\) 为似然比阈值。
例1：对某一地震高发区进行统计，地震以\(\omega_1\)类表示，正常以\(\omega_2\)类表示。统计的时间区间内，每周发生地震的概率为20%，即\(P(\omega_1)=0.2\)，当然\(P(\omega_2)=0.8\)。通常地震与生物异常反应之间有一定的联系，若用生物是否有异常反应这一观察现象来对地震进行预测，生物是否异常这一结果以模式\(x\)代表，这里\(x\)为一维特征，且只有\(x\)=“异常”和\(x\)=“正常”两种结果。假设根据观测记录，发现这种方法有以下统计结果：
地震前一周内出现生物异常反应的概率 \(=0.6\) ，即 \(P\left(x=\right.\) 异常 \(\left.\mid \omega_1\right)=0.6\)
地震前一周内出现生物正常反应的概率 \(=0.4\) ，即 \(P\left(x=\right.\) 正常 \(\left.\mid \omega_1\right)=0.4\)
一周内没有发生地震但出现生物异常的概率 \(=0.1\) ，即 \(P\left(x=\right.\) 异常 \(\left.\mid \omega_2\right)=0.1\)
一周内没有发生地震时生物正常的概率 \(=0.9\) ，即 \(P\left(x=\right.\) 正常 \(\left.\mid \omega_2\right)=0.9\)
若某日观察到明显的生物异常反应现象，此情况属于地震还是正常?
由于0.6<0.9，$$P(\omega_1|{x= 异常})<P(\omega_2|{x= 正常})$$
似然比: \(\frac{p\left(x=\text { 异常 } \mid \omega_1\right)}{p\left(x=\text { 正常 } \mid \omega_2\right)}=\frac{0.6}{0.1}=6\)
似然比阈值: \(\frac{p\left(\omega_2\right)}{p\left(\omega_1\right)}=\frac{0.8}{0.2}=4\)
似然比>似然比阈值，则第一类错误率更小，即某日观察到明显的生物异常反应现象，此情况为地震。
三、最小风险贝叶斯决策
样本\(X\)：\(d\)维随机向量 \(X=[x_1,x_2,...,x_d]^T\)（构成自然空间）
类别\(w\)：\(\Omega=\{\omega_1,\omega_2,...,\omega_c\}\) （构成状态空间\(\Omega\)）
决策 \(\alpha\)：分类时所采取的决定。决策\(\alpha_i\)表示将模式\(X\) 指判为\(\omega_i\)。
损失函数：对于真实状态为\(\omega_i\)的模式\(X\)，采取决策\(\alpha_j\)所带来的损失
若希望尽可能避免将状态\(\omega_i\)错判为\(\omega_j\) （即该分类错误损失较大），则可以将相应的\(\lambda_{ij}\)的值调大一些。
决策表：决策表的形成是困难的，需要大量的领域知识。决策表不同会导致决策结果的不同。
| \(\alpha_1\) | \(\alpha_2\) | ...... | \(\alpha_c\) | |
|---|---|---|---|---|
| \(\omega_1\) | \(\lambda_{11}=\lambda(\alpha_1,\omega_1)\) | \(\lambda_{12}=\lambda(\alpha_2,\omega_1)\) | ...... | \(\lambda_{1c}=\lambda(\alpha_c,\omega_1)\) |
| \(\omega_2\) | \(\lambda_{21}=\lambda(\alpha_1,\omega_2)\) | \(\lambda_{22}=\lambda(\alpha_2,\omega_2)\) | ...... | \(\lambda_{11}=\lambda(\alpha_c,\omega_2)\) |
| ...... | ...... | ...... | \(\lambda_{ij}\) | ...... |
| \(\omega_c\) | \(\lambda_{c1}=\lambda(\alpha_1,\omega_c)\) | \(\lambda_{c2}=\lambda(\alpha_2,\omega_c)\) | ...... | \(\lambda_{cc}=\lambda(\alpha_c,\omega_c)\) |
最小风险：把各种分类错误引起的损失考虑进去的贝叶斯决策法则，以使得期望的损失最小。
模式\(X\)的期望损失：通过对属于不同状态\(\omega_j\)的后验概率\(P(\omega_j|X)\) 采取决策\(\alpha_j\)的期望损失（期望风险）
最小风险：
若\(R(\alpha_k|X)=\min_{i=1,...,c}R(\alpha_i|X)\)，则\(\alpha=\alpha_k\)
最小风险和最小错误率贝叶斯决策法则的关系：
两类最小错误率贝叶斯决策规则
多类最小错误率贝叶斯决策规则
多类最小风险贝叶斯决策规则
考虑特殊的损失函数：\(\lambda_{ii}=0，\lambda_{ij}=1，\quad i \neq j\)
根据贝叶斯公式，将后验概率转化为先验概率来表示
上面公式分母与\(i\)无关，也就与分类无关，故\(R_i(X)\)又可转化表示为
当\(X \in \omega_i\)时，应满足
这时最小风险贝叶斯决策准则就是最小错误率贝叶斯准则，所以最小风险准则是最小错误率准则的推广与扩展，二者意义上是一致的。
例2：已知某个局部组织中有异常细胞，且正常细胞\(\omega_1\)和异常细胞\(\omega_2\)的先验概率为\(P(\omega_1)=0.9\)和\(P(\omega_2)=0.1\) 。现给一个待识别的细胞，其观测值为\(x\)，从类条件概率密度函数中可以查到：\(P(x|\omega_1)=0.2\)，\(P(x|\omega_2)=0.4\)。
我们给定损失值 \(\Lambda=(\lambda_{11},\lambda_{12},\lambda_{21},\lambda_{22})=(0,6,1,0)\)
施加代价后的贝叶斯风险为：
显然，\(R_1>R_2\)，应把\(x\)判断为异常细胞。
四、扩展案例
设有19人进行体检，结果如下表。但事后发现4人忘了写性别，试问这4人是男是女？
| 序号 | 身高 | 体重 | 性别 | 序号 | 身高 | 体重 | 性别 |
|---|---|---|---|---|---|---|---|
| 1 | 170 | 68 | 男 | 11 | 140 | 62 | 男 |
| 2 | 130 | 66 | 女 | 12 | 150 | 64 | 女 |
| 3 | 180 | 71 | 男 | 13 | 120 | 66 | 女 |
| 4 | 190 | 73 | 男 | 14 | 150 | 66 | 男 |
| 5 | 160 | 70 | 女 | 15 | 130 | 65 | 男 |
| 6 | 150 | 66 | 男 | 16 | 140 | 70 | α？ |
| 7 | 190 | 68 | 男 | 17 | 150 | 60 | β？ |
| 8 | 210 | 76 | 男 | 18 | 145 | 65 | γ？ |
| 9 | 100 | 58 | 女 | 19 | 160 | 75 | δ？ |
| 10 | 170 | 75 | 男 |
总结
朴素贝叶斯算法的主要原理基本讲清楚了，这里对朴素贝叶斯的优缺点做一个总结。
朴素贝叶斯的主要优点有：
1）朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
2）对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练。
3）对缺失数据不太敏感，算法也比较简单，常用于文本分类。
朴素贝叶斯的主要缺点有：
1） 理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
2）需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
3）由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。
4）对输入数据的表达形式很敏感。
